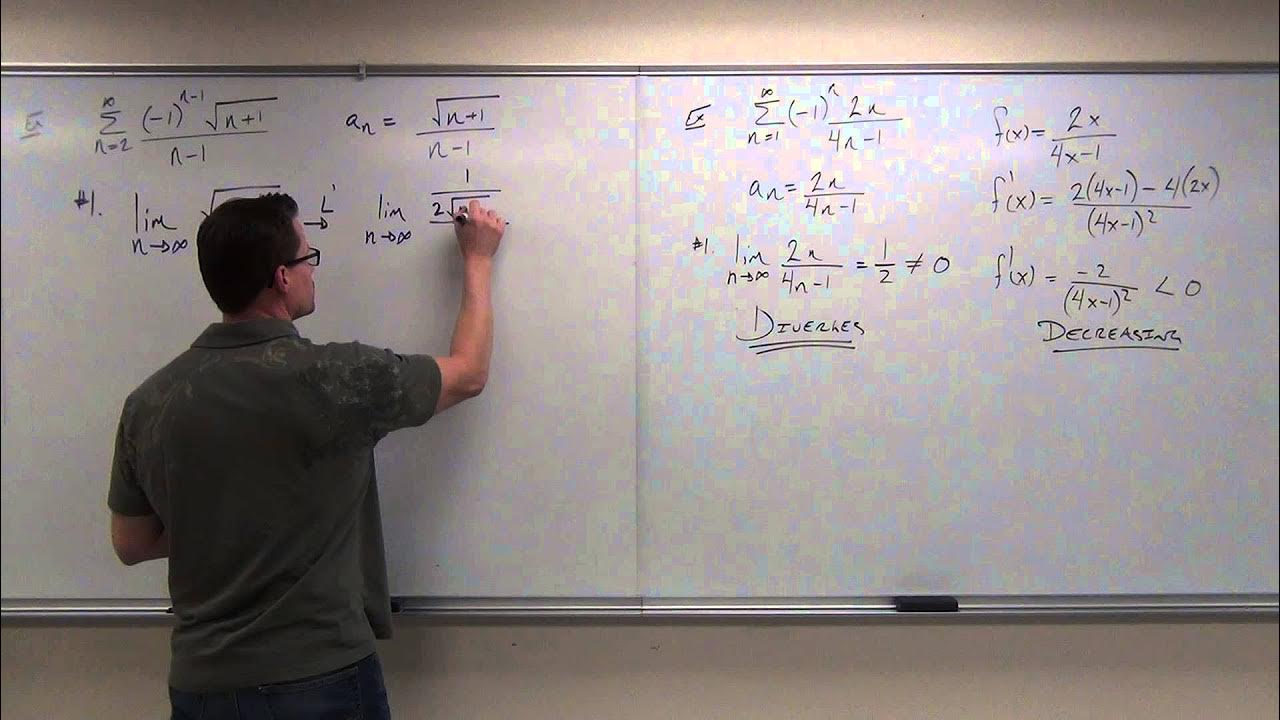Alternating Series Test and Error for Alternating Series
TLDRThis video script delves into the Alternating Series Test for convergence, explaining its three key components: the series must alternate, the limit of the nth term must approach zero, and the terms must decrease. It uses examples to illustrate the test's application and highlights the importance of the decreasing nature of terms. The script also touches on the error term associated with alternating series, emphasizing that the error is at most the absolute value of the first omitted term, providing a clear and concise method to estimate the error in such series.
Takeaways
- 📚 The alternating series test involves three main criteria: the series must alternate, the limit of the absolute value of its terms as \( n \) approaches infinity must be zero, and the terms must decrease in absolute value.
- 🔍 To apply the alternating series test, first ensure the series alternates, which is often straightforward due to the presence of a term like \( (-1)^n \).
- 🎯 The second requirement is to find the limit of \( a_n \) as \( n \) approaches infinity, which should equal zero for the series to be considered convergent by this test.
- 📉 The third requirement is that the terms \( a_n \) must be monotonically decreasing, which is crucial for the series to converge according to the alternating series test.
- 🚫 If the limit of \( a_n \) is not zero, the series does not pass the alternating series test, but this does not necessarily mean it diverges; other tests may be required.
- 🌰 An example given in the script is the series \( \sum_{n=0}^{\infty} \frac{(-1)^n}{\sqrt{n}} \), which converges because it meets all three criteria of the alternating series test.
- 📌 To show a function is decreasing, one can take its derivative and show that it is negative, as demonstrated with \( f(x) = \frac{1}{\sqrt{x}} \) where \( f'(x) = -\frac{1}{2x^{3/2}} \).
- 📊 The script also discusses an example that fails the alternating series test, \( \sum_{n=0}^{\infty} \frac{n \cdot \cos(\pi n)}{n + 5} \), because the limit of \( \frac{n}{n+5} \) as \( n \) approaches infinity is 1, not zero.
- ❗ The nth term test for divergence states that if the limit of the nth term of a series does not approach zero, the series must diverge.
- 🔢 The error term in an alternating series approximation is at most the absolute value of the first term not included in the approximation.
- 🧩 An example of calculating the error term is provided, where using the first three non-zero terms of the series \( \sum_{n=1}^{\infty} \frac{1}{n(1+n)^3} \) gives an error of at most \( \frac{1}{6^3} \) or \( \frac{1}{216} \).
Q & A
What is an alternating series?
-An alternating series is a series where the terms alternate in sign, typically represented as the sum from 0 to infinity of (-1)^n times a_n, where a_n is a sequence of positive terms.
What are the three main parts of the alternating series test?
-The three main parts of the alternating series test are: 1) The series must alternate, 2) The limit as n approaches infinity of a_n must equal zero, and 3) The terms a_n must decrease in absolute value.
Why is it important to check if the series alternates before applying the alternating series test?
-It is important to check if the series alternates because the alternating series test is specifically designed for series with alternating signs. If the series does not alternate, this test is not applicable.
What does the limit of the terms of an alternating series need to be for the series to converge according to the test?
-For an alternating series to converge according to the test, the limit of the terms a_n as n approaches infinity must be zero.
How can you show that the terms of an alternating series are decreasing?
-You can show that the terms of an alternating series are decreasing by taking the derivative of the function representing the terms and proving that it is negative, indicating that the function is decreasing.
Can you provide an example of an alternating series that converges according to the alternating series test?
-An example of a converging alternating series is the sum from 0 to infinity of (1/√n), which alternates in sign and has terms that decrease and approach zero as n goes to infinity.
What happens if the limit of the terms of an alternating series does not equal zero?
-If the limit of the terms of an alternating series does not equal zero, the alternating series test cannot be used to conclude convergence. The series might still converge or diverge, but a different test must be used to determine its behavior.
What is the nth term test for divergence, and how does it relate to the alternating series test?
-The nth term test for divergence states that if the limit of the nth term of a series is not zero, then the series must diverge. It is a complementary test to the alternating series test, which tests for convergence, not divergence.
How can you estimate the error involved in using an alternating series with a finite number of terms?
-The error involved in using an alternating series with a finite number of terms is at most the absolute value of the first term that you leave off, which is the next term in the series after the last one you included.
Can you give an example of how to calculate the error term for an alternating series approximation?
-For the series sum from 1 to infinity of 1/(1 + n)^3, using the first three nonzero terms, the error term is at most the absolute value of the fourth term, which is 1/65.
Outlines
📚 Alternating Series Test and Convergence
This paragraph introduces the concept of the alternating series test for convergence, which is a method to determine if an infinite series with alternating signs converges. The speaker explains that the test involves three key parts: ensuring the series alternates, finding that the limit of the absolute value of the nth term as n approaches infinity equals zero, and proving that the terms of the sequence decrease. An example is given with the series 1/√n, which meets all criteria and thus converges. The speaker also discusses the importance of showing the sequence's terms decrease, using the derivative test to confirm this for the given example.
🔍 Testing for Divergence with the nth Term Test
The second paragraph delves into the use of the nth term test for divergence, contrasting it with the alternating series test. The speaker uses the example of the series n * cos(πn) / (n + 5) to illustrate the process. Initially, it's shown that the series alternates, but the limit of the nth term as n approaches infinity does not equal zero, disqualifying it from the alternating series test. The nth term test is then applied, revealing that the series diverges since the limit of the nth term is not zero. The speaker emphasizes that while the nth term test always tests for divergence, it does not guarantee that a series will diverge if the limit is not zero.
📉 Understanding Alternating Series Error
In this paragraph, the concept of error in the context of alternating series is discussed. The speaker explains that the error in using an alternating series is at most the absolute value of the first term omitted, which is a simple and memorable rule. An example problem is presented, where the first three nonzero terms of the series 1^n / (1 + n)^3 are used to approximate the sum, and the error is calculated by considering the absolute value of the first omitted term, which is 1/65 in this case. The summary underscores the ease of calculating the error in alternating series approximations.
Mindmap
Keywords
💡Alternating Series
💡Error Term
💡Convergence
💡Divergence
💡nth Term Test
💡Limit
💡Decreasing Terms
💡Absolute Value
💡P-Series
💡Derivative
Highlights
The series test for alternating series involves checking if the series alternates, which is usually straightforward.
The second part of the test is to find the limit as n approaches infinity of the absolute value of the nth term, which must equal zero.
The third part requires the terms of the series to decrease, eventually leading to convergence if the conditions are met.
An example series is given as the sum from 0 to infinity of 1/√n, which is shown to converge by the alternating series test.
The limit of 1/√n as n approaches infinity is zero, satisfying one of the criteria for the alternating series test.
To be picky about the decreasing part, taking the derivative of 1/√x shows the function is decreasing, confirming the series converges.
Another example series with n*cos(π*n)/(n+5) is analyzed, and it's determined that it does not satisfy the alternating series test due to the limit approaching one.
The nth term test for divergence is suggested as an alternative when the alternating series test is not applicable.
The series n*cos(π*n)/(n+5) is shown to diverge by the nth term test since the limit of the nth term does not approach zero.
The concept of the alternating series error term is introduced, stating that the error is at most the absolute value of the first term left off.
An example problem calculates the error using the first three nonzero terms of the sum from one to infinity of 1/(1+n)^3.
The error in the approximation is at most 1/65, demonstrating how to apply the concept of the alternating series error term.
The transcript emphasizes the importance of understanding the conditions for the alternating series test and its implications for convergence.
The transcript also highlights the use of derivatives to prove that a function is decreasing, a key step in the alternating series test.
The nth term test is presented as a definitive method to determine divergence when the alternating series test is inconclusive.
The transcript provides a clear explanation of how to apply the alternating series test and its error term in practical examples.
The importance of the limit approaching zero for the nth term in determining the convergence of an alternating series is underscored.
The transcript concludes with a summary of the key points about alternating series, their tests for convergence, and error term calculations.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: