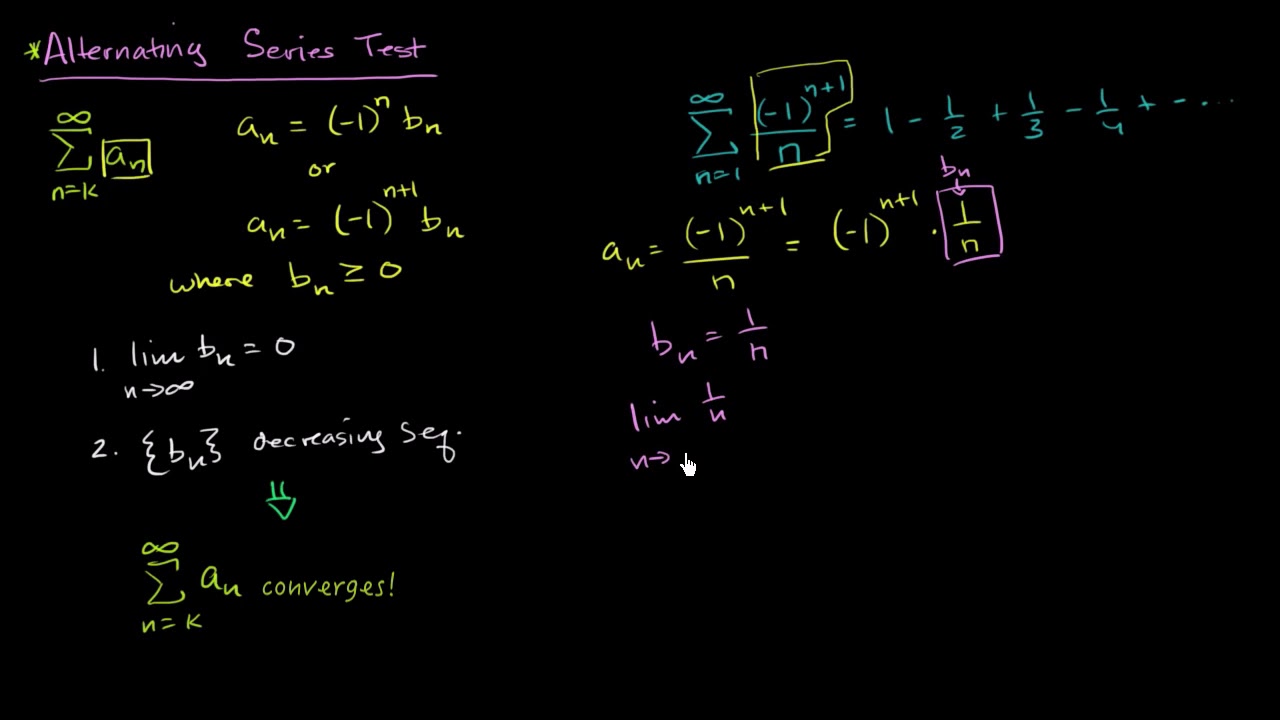Calculus 2 Lecture 9.5: Showing Convergence With the Alternating Series Test, Finding Error of Sums
TLDRThis educational video script delves into the concept of alternating series in calculus, explaining the fundamental characteristics of such series where terms alternate in sign. It introduces the alternating series test, which assesses convergence by ensuring the sequence of terms is decreasing and the limit of the sequence as n approaches infinity is zero. The script provides step-by-step examples, illustrating how to apply the test to determine if a series converges, and highlights the difference between divergent harmonic series and convergent alternating harmonic series. Additionally, it discusses estimating the sum of a series by calculating the error between the partial sum and the actual sum of a convergent alternating series, demonstrating how to find the number of terms needed to achieve a desired level of accuracy.
Takeaways
- 📚 The script discusses the concept of alternating series, which are series where sequential terms alternate in sign (positive, negative, positive, negative, etc.).
- 🔍 An alternating series can often be expressed as -1^n * a_n, where a_n is a series of positive terms.
- 📝 The Alternating Series Test is introduced to determine the convergence of alternating series. It involves two main conditions: the sequence of positive terms must be decreasing, and the limit of a_n as n approaches infinity must be zero.
- 📉 The test for convergence involves checking if a_(n+1) is less than or equal to a_n, indicating that the sequence of terms is decreasing.
- 🧩 The script provides an example of an alternating series and demonstrates how to apply the Alternating Series Test to determine its convergence.
- 🔢 The concept of 'error' in the context of series is explained, which refers to the difference between the sum of the series and a partial sum.
- 📌 The error for an alternating series can be estimated to be less than or equal to the next term in the series (1/(n+1)! in the given example).
- 📐 The script explains how to use the error bound to determine the number of terms needed for the partial sum to be within a certain accuracy of the actual sum of the series.
- 📘 An example calculation is performed to find the partial sum and its corresponding error, demonstrating the process of finding how many terms are needed to achieve a specific level of accuracy.
- 🤔 The importance of understanding the underlying concepts rather than just memorizing procedures is emphasized, particularly in grasping why the Alternating Series Test works and how to apply it.
Q & A
What is an alternating series?
-An alternating series is a series where sequential terms alternate in sign, typically represented by positive and negative terms in a repeating pattern, such as positive, negative, positive, negative, and so on.
Can you give an example of an alternating series?
-An example of an alternating series is the alternating harmonic series, which is 1 - 1/2 + 1/3 - 1/4 + 1/5 - ..., where the signs of the terms alternate between positive and negative.
What is the alternating series test used for?
-The alternating series test is used to determine the convergence of an alternating series. It provides a set of conditions that, if met, indicate that the series will converge.
What are the conditions for the alternating series test?
-The conditions for the alternating series test are: 1) The limit of the absolute value of the terms (a_n) as n approaches infinity must be zero. 2) The sequence of terms must be decreasing in magnitude for all n.
How does the alternating series test relate to the divergence test?
-The alternating series test uses a modified version of the divergence test, focusing on the limit of the sequence of positive terms (a_n) rather than the entire series. If the limit of a_n as n approaches infinity is zero and the sequence is decreasing, the series is convergent.
What is the difference between a harmonic series and an alternating harmonic series?
-The harmonic series is a series where each term is the reciprocal of a natural number, such as 1 + 1/2 + 1/3 + ..., and it diverges. The alternating harmonic series is the same but with alternating signs, like 1 - 1/2 + 1/3 - 1/4 + ..., and it converges.
Why is it important to show that a sequence is decreasing when applying the alternating series test?
-Showing that a sequence is decreasing is important because it ensures that the terms of the series are getting smaller and approaching zero. This is a necessary condition for the convergence of an alternating series, as it prevents the series from oscillating indefinitely.
How can you determine if a series is alternating?
-A series is alternating if it can be expressed in the form of -1^n * a_n, where a_n is a sequence of positive terms. The key indicator is the presence of the (-1)^n factor, which causes the signs of the terms to alternate.
What is the concept of error in the context of series convergence?
-In the context of series convergence, error refers to the difference between the sum of the series (S) and a partial sum (S_n). It represents how close the partial sum is to the actual sum of the series.
How can you estimate the error for an alternating series?
-For an alternating series, the error (R_n) can be estimated by ensuring that the next term in the sequence (a_(n+1)) is less than a given tolerance level for error. The error is guaranteed to be less than or equal to this next term in the sequence.
Can you find the sum of a series without actually summing all terms?
-Yes, for a convergent alternating series, you can approximate the sum by summing a finite number of terms and using the concept of error to determine how close the partial sum is to the actual sum of the series.
Outlines
🔍 Introduction to Alternating Series Test
The video script begins with an introduction to the concept of alternating series, explaining that these are series where the signs of sequential terms alternate between positive and negative. The instructor provides an example of an alternating series and distinguishes it from a sequence by emphasizing the addition of terms. The alternating harmonic series is introduced as a specific type of series that can be written as the product of (-1)^n and a positive sequence, highlighting its importance in the study of series.
📚 Understanding Alternating Series and Their Properties
The script continues to explore the nature of alternating series, focusing on their defining characteristic of alternating signs. It discusses how these series can be broken down into a product of (-1)^n and a sequence of positive terms, using the harmonic series as an example. The instructor also explains the concept of convergence for alternating series and introduces the alternating series test, which involves checking if the sequence of positive terms is decreasing and if its limit as n approaches infinity is zero.
📉 The Alternating Series Test and Its Criteria
The instructor delves into the specifics of the alternating series test, outlining the two main criteria for convergence: the sequence of positive terms must be decreasing, and the limit of the sequence as n approaches infinity must be zero. These points are illustrated with examples, and the script emphasizes the importance of understanding the behavior of the sequence of positive terms in determining the convergence of an alternating series.
🎯 Graphical Explanation of Alternating Series Convergence
The script provides a graphical explanation of why alternating series converge. It likens the process of adding and subtracting terms in an alternating series to a 'ping-pong match,' where the partial sums get closer and closer to a single value as n approaches infinity. This visual analogy aims to help viewers understand the concept of convergence in alternating series without a formal proof.
📝 Applying the Alternating Series Test to Examples
The instructor applies the alternating series test to specific examples, demonstrating how to determine if a given series is convergent by checking the limit of the sequence of positive terms and whether the sequence is decreasing. The script highlights the importance of these steps in confirming the convergence of an alternating series.
🤔 Error Estimation in Alternating Series
The script introduces the concept of error estimation for alternating series, explaining that there will be an error between the partial sum and the actual sum of the series if the series converges. It discusses how to find this error and emphasizes that error estimation is only applicable to convergent alternating series.
🔢 Calculating Partial Sums and Estimating Errors
The instructor explains how to calculate partial sums and estimate errors for alternating series. It provides a step-by-step guide on determining the number of terms needed to achieve a desired level of accuracy, using the error term and the properties of the series to ensure that the partial sum is within a specified tolerance of the actual sum.
📚 Summary of Alternating Series Concepts
The script concludes with a summary of the key concepts related to alternating series, including their definition, the alternating series test for convergence, and the process for estimating errors in partial sums. It reinforces the importance of understanding these concepts for working with alternating series.
Mindmap
Keywords
💡Alternating Series
💡Alternating Series Test
💡Convergence
💡Divergence Test
💡Decreasing Sequence
💡Factorial
💡Harmonic Series
💡Error
💡Partial Sum
💡Limit
Highlights
Introduction to alternating series and their definition.
Alternating series typically involve sequential terms that alternate signs.
Example of an alternating series and how it is constructed.
Explanation of how to represent alternating series with -1 raised to the power of n.
Alternating series can be written as a product of -1^n and a series of positive terms.
Introduction to the alternating series test and its conditions.
The importance of the sequence of positive terms (a_n) in the alternating series test.
Condition for convergence: a_(n+1) must be less than or equal to a_n, indicating a decreasing sequence.
The Divergence test's role in the alternating series test.
Proof of why an alternating series converges through the concept of partial sums.
Graphical explanation of the convergence of alternating series using a 'ping-pong' analogy.
Demonstration of applying the alternating series test to a specific example.
Comparison between the harmonic series and the alternating harmonic series.
Discussion on the difference between proving a series diverges and applying the alternating series test.
Explanation of how to find the error in an alternating series when not all terms are summed.
Practical application of the error bound in alternating series to approximate the sum.
Process of determining the number of terms needed to achieve a desired accuracy.
Final summary of the alternating series test, its conditions, and the concept of error.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: