Calculus BC – 10.7 Alternating Series Test for Convergence
TLDRIn this calculus lesson with Mr. Bean, students delve into the concept of alternating series, learning to apply the Alternating Series Test to determine convergence. The lesson covers identifying series as alternating and verifying two key conditions: the limit of the series' term approaching zero and the series' terms decreasing in absolute value. Examples illustrate the process, including the convergence of the alternating harmonic series and the divergence of a series with a non-zero limit. The lesson also addresses series that may appear alternating but are not, due to constant positive terms, emphasizing the importance of recognizing true alternating patterns for accurate convergence assessment.
Takeaways
- 📚 The lesson is about the Alternating Series Test, a method to determine if an alternating series converges or not.
- 🔍 An alternating series is characterized by terms that switch between positive and negative, often represented by \((-1)^n\) raised to some power.
- 🎯 The two main conditions for an alternating series to converge are: (1) the limit of \(a_n\) as \(n\) approaches infinity must equal zero, and (2) the absolute value of successive terms must decrease.
- 📉 To check if the series is decreasing, one can either plug in values to observe the trend or manipulate the terms to ensure the ratio of successive terms is less than one.
- 📝 The script provides an example of an alternating harmonic series, which converges when alternating, contrary to the non-alternating harmonic series which diverges.
- 📉 Another method to verify a decreasing series is by taking the first derivative of \(a_n\) and checking if it's negative, though this method is considered cumbersome and can be avoided if simpler methods are available.
- 🔢 The script demonstrates the process of checking the limit and decreasing nature of series through several examples, including series with \(n+1\) in the term which affects the starting sign of the series.
- ❌ A series that does not meet the first condition (limit not equaling zero) is guaranteed to diverge, and there's no need to check the second condition.
- 🌐 The script also covers a series involving cosine functions, illustrating how the alternating nature of cosine can create an alternating series when multiplied by \((-1)^n\).
- 🚫 An example is given where a series is not alternating because the combination of terms always results in a positive value, thus failing to meet the criteria for an alternating series.
- 📚 The lesson concludes with an encouragement to practice the learned concepts and prepare for mastery checks.
Q & A
What is the main topic of Mr. Bean's calculus lesson?
-The main topic of the lesson is the concept of alternating series and the alternating series test, which helps determine if a series is converging or not.
What is an alternating series?
-An alternating series is a series where the terms switch between positive and negative, often represented by a function that involves (-1)^n multiplied by some nth power.
What are the two conditions that must be met for an alternating series to be considered converging?
-The two conditions are: 1) The limit of the function a_n as n approaches infinity must equal zero, and 2) The succeeding term must be smaller than the previous term, indicating that the series is decreasing.
How can you check if a series is decreasing?
-One way to check if a series is decreasing is by taking the first derivative of the function and seeing if it is negative. Another way is to plug in numbers and observe if each term gets smaller than the previous one.
What is the significance of the absolute value in the condition that the succeeding term must be smaller than the previous term?
-The absolute value ensures that the comparison is based on the magnitude of the terms, regardless of their sign, confirming that the series is indeed decreasing.
How does Mr. Bean suggest checking if a function is decreasing without taking the derivative?
-Mr. Bean suggests plugging in numbers to see if the terms get smaller as n increases, or by creating a ratio of a_n+1 to a_n and ensuring that this ratio is less than one.
What is an example of an alternating series given in the script?
-An example given is the series involving (-1)^n where n ranges from 1 to infinity, which is an alternating harmonic series that converges.
Why does the alternating harmonic series converge instead of diverge?
-The alternating harmonic series converges because it meets both conditions of the alternating series test: the limit of the terms goes to zero, and the terms are decreasing.
What happens if the limit of the terms in an alternating series does not equal zero?
-If the limit of the terms does not equal zero, the series does not converge, and there is no need to check the second condition regarding the terms being in decreasing order.
Can a series with a cosine function be an alternating series?
-Yes, a series can be an alternating series if the cosine function causes the terms to alternate between positive and negative values, as seen in the example where cos(nπ) alternates between -1 and 1.
Why is the series involving both (-1)^n and cos(nπ) not an alternating series?
-The series is not an alternating series because the product of (-1)^n and cos(nπ) always results in positive terms, meaning there is no alternation between positive and negative values.
Outlines
📚 Introduction to Alternating Series Test
This paragraph introduces the concept of alternating series in calculus, presented by a character named Mr. Bean. The focus is on the alternating series test, which determines the convergence of a series that oscillates between positive and negative values. The typical form of an alternating series is highlighted, often involving a sequence like (-1)^n * (1/n^n). Two key conditions for convergence are discussed: the limit of the series' terms as n approaches infinity must be zero, and each term must be smaller than the previous term, indicating a decreasing sequence. The paragraph also touches on methods to verify the decreasing nature of the series, such as taking derivatives or comparing terms directly.
🔍 Analyzing the Alternating Series with Examples
The second paragraph delves deeper into the analysis of alternating series with specific examples. It starts with an alternating harmonic series, demonstrating that while the harmonic series diverges, the alternating version converges. The explanation includes checking the limit condition and verifying the decreasing nature of the series' terms. The paragraph continues with another example involving a series with a different form but still alternating, where the limit condition is met, and a ratio test confirms the series is decreasing. The discussion also includes a series that does not meet the first condition of the limit test, leading to its divergence, and concludes with a trick to simplify the comparison of terms for the decreasing condition.
📉 Dealing with Series Without Obvious Alternation Patterns
This paragraph addresses series that do not immediately appear to be alternating due to the absence of the typical (-1)^n pattern. It uses the cosine function as an example to illustrate how a series can still be alternating. The explanation includes calculating the limit of the series' terms and confirming their decreasing nature. The paragraph also presents a non-alternating series involving both a power term and a cosine function, which always results in positive terms, thus failing the alternating series test. The summary emphasizes the importance of recognizing the underlying pattern of alternation, even when it's not explicitly presented by a (-1)^n factor.
Mindmap
Keywords
💡Alternating Series
💡Alternating Series Test
💡Convergence
💡Limit
💡Decreasing Function
💡First Derivative
💡Horizontal Asymptote
💡Harmonic Series
💡nth Term Test
💡Ratio Test
💡Cosine Function
Highlights
Introduction to the concept of alternating series and the alternating series test in calculus.
Explanation of alternating series characterized by a pattern of positive and negative terms.
Description of the typical form of an alternating series involving (-1)^n raised to a power.
Two conditions for an alternating series to converge: limit of a_n approaching zero and the sequence being decreasing.
Method to check if a series is decreasing by taking the first derivative and ensuring it is negative.
Alternative method to verify a decreasing series by plugging in numbers and observing the trend.
Technique to prove a series is decreasing by creating a ratio that must be less than one.
Example of an alternating harmonic series and its convergence when alternating.
Demonstration of the alternating series test with the harmonic series, meeting both convergence conditions.
Second example with a series involving (n+1)^2 in the denominator, and its convergence analysis.
Use of ratio test to confirm the decreasing nature of the second example series.
Third example with a series that does not meet the first condition for convergence, thus diverging.
Clarification of the nth term test and its implications for series divergence when the limit does not equal zero.
Fourth example of an alternating series with cosine function, demonstrating convergence through the test.
Final example illustrating a series that is not alternating due to the constant positive product of terms.
Conclusion of the lesson with a summary of the alternating series test and its application in various examples.
Transcripts
Browse More Related Video

AP Calculus BC Lesson 10.7

Alternating Series
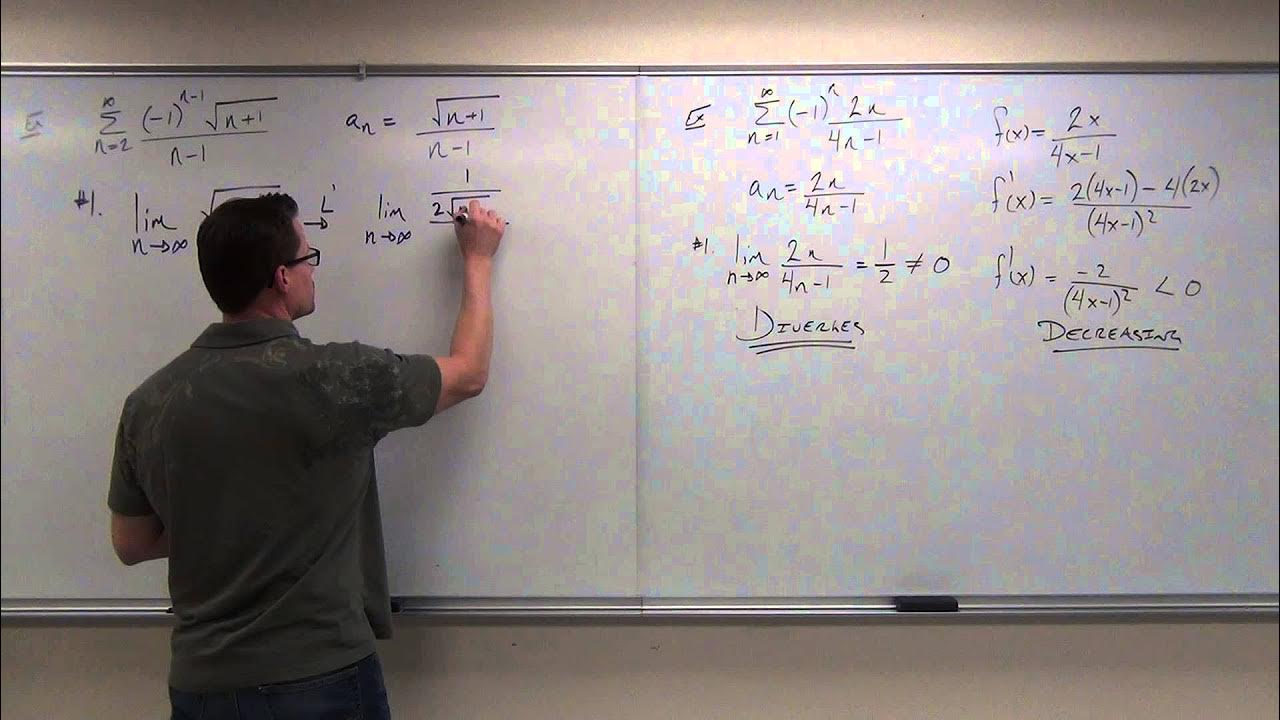
Calculus 2 Lecture 9.5: Showing Convergence With the Alternating Series Test, Finding Error of Sums
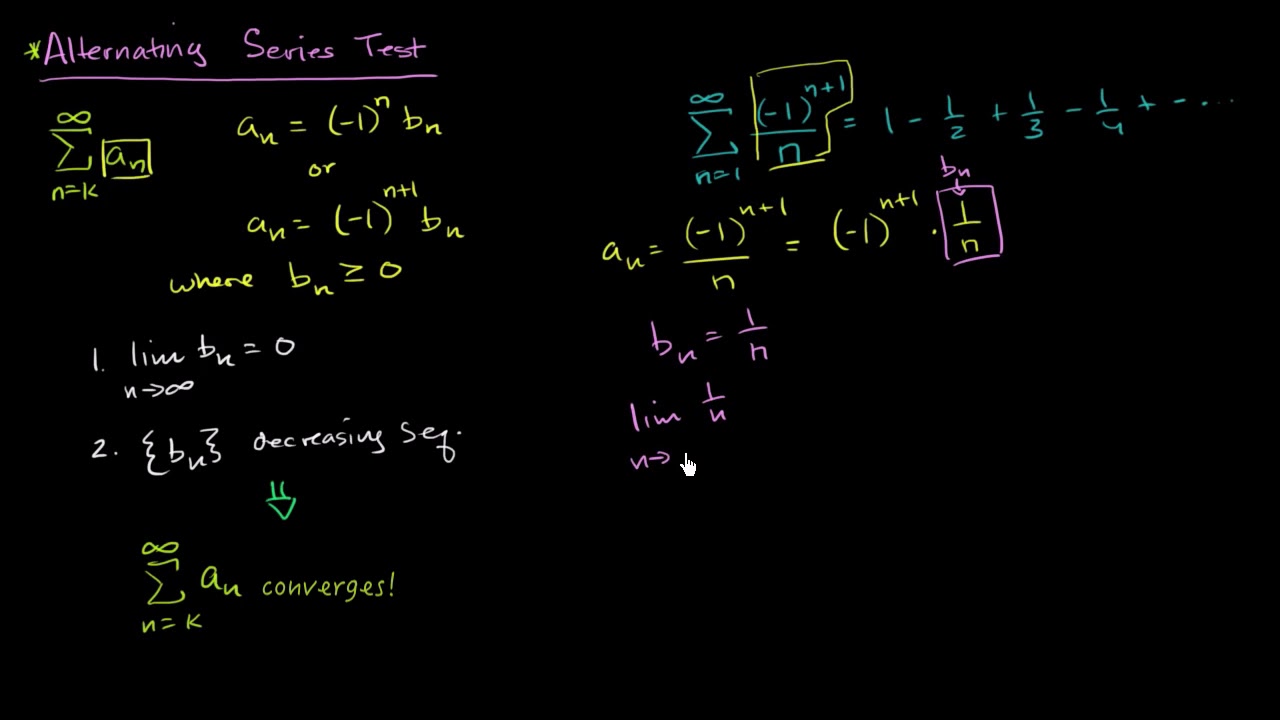
Alternating series test | Series | AP Calculus BC | Khan Academy

Alternating Series Test and Error for Alternating Series

Lesson 20 - Alternating Series Test (Calculus 2 Tutor)
5.0 / 5 (0 votes)
Thanks for rating: