Math 1325 Lecture 9 4 - Derivative Formulas
TLDRThe lecture transcript introduces various shortcut methods for finding derivatives of functions, which are essential for calculus students. The power rule is explained first, where the derivative of x raised to a power is the power multiplied by x to the power of one less. The constant rule states that the derivative of a constant function is always zero, as the slope of a horizontal line is zero. The coefficient rule allows for the simplification of derivatives by pulling constants out of functions. The rules for derivatives of sums and differences of functions are also covered, where the derivative of a sum or difference is the sum or difference of the individual derivatives. Examples are provided to illustrate these rules, emphasizing the importance of understanding the underlying concepts and practicing the application of these shortcuts for solving derivatives. The transcript also touches on the notation for derivatives and the concept of negative exponents, which are treated as reciprocals in the context of calculus.
Takeaways
- 📚 To find derivatives using the definition, apply the limit as h goes to 0 of the difference quotient (f(x+h) - f(x))/h.
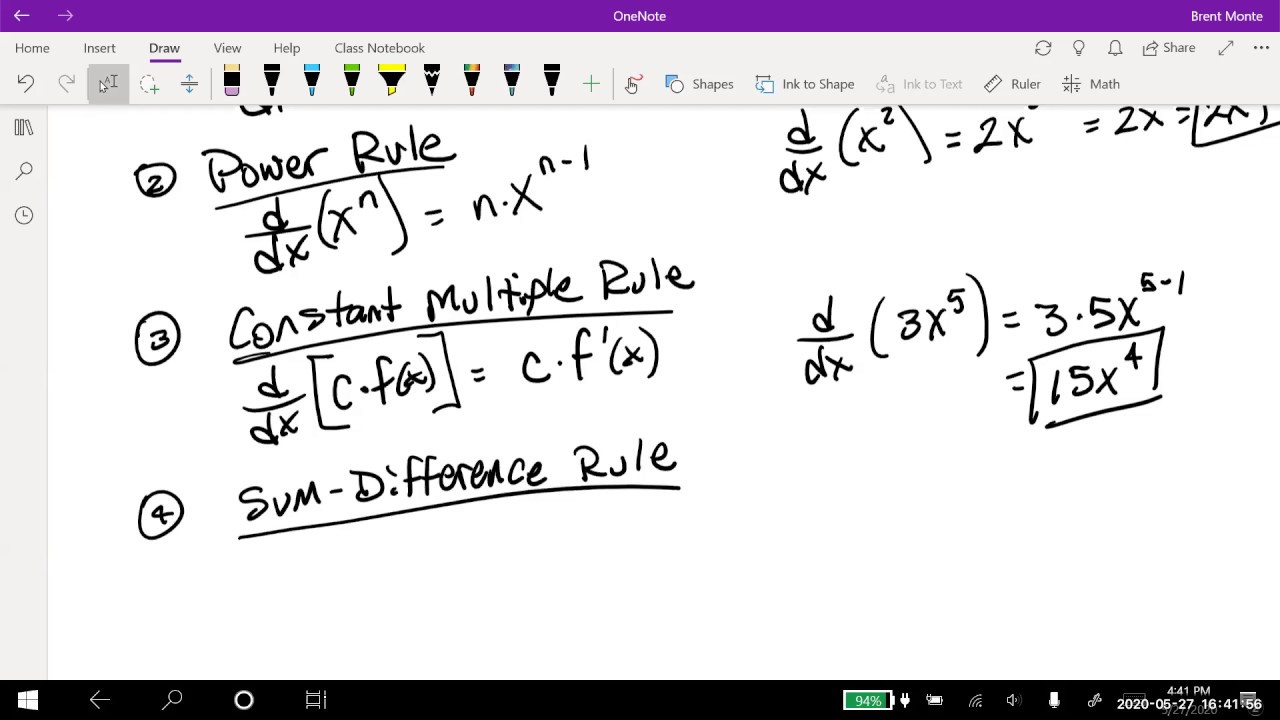
- ✅ The power rule states that the derivative of x^n is nx^(n-1), where you pull the power down as a multiplier and subtract 1 from the exponent.
- 🚫 The constant rule indicates that the derivative of a constant function is always 0, since the slope of a horizontal line is zero.
- 🔢 The coefficient rule allows you to pull a constant out of a function and then apply it to the derivative of the function inside.
- 🔁 For sums and differences of functions, you can take the derivative of each function separately and then add or subtract the results.
- 📈 The derivative of a function represents the rate of change or the slope of the function at a specific point.
- 📉 Any function to the power of 0 equals 1, which simplifies the derivative calculation when dealing with terms raised to the power of 0.
- 🎓 Negative exponents mean to reciprocate, so x^-n is the same as 1/(x^n).
- 🛠 Fractional exponents can be treated as powers, where the numerator is the exponent and the denominator is the root.
- 📐 Radicals or roots can be rewritten with an exponent, and if the root is in the denominator, it can be converted to a negative exponent.
- ✍ The notation G' or dG/dT both represent the derivative of G with respect to T.
- 📈 When differentiating a sum or difference, you can treat each term independently and then combine the derivatives as required.
Q & A
What is the process for finding derivatives using the definition?
-The process involves applying the limit as H goes to 0 of the difference quotient, which is f(x + h) - f(x) divided by h.
What is the power rule for derivatives?
-The power rule states that the derivative of x raised to a power is the power multiplied by x to the power one less than the original power.
How does the constant rule apply to derivatives?
-The constant rule states that the derivative of a constant function is always 0, as constants do not change and thus have no rate of change.
What is the coefficient rule in the context of derivatives?
-The coefficient rule allows you to pull a constant coefficient out of a function and then apply it to the derivative of the remaining function.
How do you find the derivative of a sum or difference of functions?
-You can take the derivative of each function separately and then add or subtract the results, as the derivative of a sum or difference equals the sum or difference of the derivatives.
What is the derivative of x cubed?
-The derivative of x cubed is 3x squared, following the power rule by bringing down the exponent 3 and subtracting 1, resulting in 2.
How does the power rule apply to negative exponents?
-Negative exponents in the power rule mean that the term is reciprocated. For example, x to the negative 2 becomes 1 over x squared.
What does the graph of a constant function look like, and why is its derivative 0?
-The graph of a constant function is a horizontal line. Its derivative is 0 because the slope of a horizontal line is 0, indicating no change in the function's value.
How do you find the derivative of a function that includes a fraction with an exponent?
-You rewrite the fraction with an exponent as a negative exponent, which reciprocates the term, and then apply the power rule to the variable part of the expression.
What notations are commonly used to represent the derivative of a function G with respect to T?
-The derivative of G with respect to T can be represented as either G'(T) or dG/dT, both indicating the derivative of G at T.
How is the derivative of a polynomial function treated?
-The derivative of a polynomial function is found by taking the derivative of each term and then adding or subtracting them according to the polynomial's operations.
What happens to the derivative of a constant term within a function?
-The derivative of a constant term within a function is always zero, as constants do not vary and thus their rate of change is non-existent.
Outlines
📚 Introduction to Derivatives and Power Rule
This paragraph introduces the concept of derivatives and the method of finding them using the definition involving the limit as H approaches 0 of the difference quotient. It then transitions into learning derivative shortcuts for various function types. The power rule is explained, which involves finding the derivative of a variable raised to a power by bringing the power down as a multiplier and reducing the exponent by 1. An example of differentiating x cubed to get 3x squared is provided. Additionally, the constant rule, which states that the derivative of a constant function is always 0, is introduced.
🔢 Derivative Rules: Constant, Coefficient, and Sum/Difference
The paragraph delves into the coefficient rule, where a constant is multiplied by a function, and the constant can be factored out when taking the derivative. The sum and difference rules are also covered, explaining that derivatives of functions that are sums or differences can be found by differentiating each term and then adding or subtracting the results. The concept of derivatives as rates of change or slopes is reinforced with a graphical representation of a constant function, which has a derivative of 0 as it is a horizontal line. Practice problems are suggested for the audience to solve, emphasizing the importance of applying these rules to understand derivatives better.
🧮 Applying Derivative Rules to Practice Problems
This section focuses on applying the previously mentioned derivative rules to solve practice problems. It covers the process of differentiating terms involving power, constant, and coefficient rules. The approach to finding derivatives of sums and differences of functions is also demonstrated. Specific examples include differentiating 3x + 5, which simplifies to 3x since the derivative of a constant is 0, and differentiating a more complex expression involving x cubed, x squared, and a constant. The process emphasizes the importance of breaking down expressions into their constituent parts and applying the appropriate rules to find the derivative of each part before combining them.
Mindmap
Keywords
💡Derivative
💡Power Rule
💡Constant Rule
💡Coefficient Rule
💡Sum and Difference Rule
💡Limit
💡Difference Quotient
💡Polynomial
💡Exponent
💡Reciprocal
💡Root
Highlights
Introduction to finding derivatives using the definition with the limit as H approaches 0 of the difference quotient.
The Power Rule for derivatives, where the function is X raised to a power, and the derivative is the power times X to the power minus one.
The Constant Rule, which states that the derivative of a constant function is always zero.
The Coefficient Rule, allowing the pulling out of constants from a function before taking the derivative.
Sum and Difference Rule for derivatives, where the derivative of a sum or difference of functions is the sum or difference of their derivatives.
Example problems demonstrating the application of the Power Rule for various exponents, including fractions and negative exponents.
Explanation of the meaning behind the Constant Rule, relating the derivative as a rate of change or slope, and how it equates to zero for a constant function.
Practice problems for the Coefficient Rule, illustrating how to handle constants and their derivatives within functions.
Clarification on converting between radical and exponential form, particularly for square roots and negative exponents.
Different notations for derivatives, such as G'(T) or D(G)/DT, indicating the derivative of G with respect to T.
Derivatives of sums and differences, demonstrated through example problems, emphasizing the process of differentiating each term separately.
Explanation of the derivative of a constant, which is always zero, and its implication in simplifying derivative expressions.
The process of differentiating polynomials by applying the Power Rule to each term and then combining the results.
Emphasis on the importance of showing work when asked to solve a derivative using the definition, as it will be required on tests.
The concept that the derivative of any function can be found using shortcuts or formulas, but the fundamental process should be understood.
The reminder that negative exponents mean to reciprocate, converting the expression to its reciprocal form.
The suggestion to pause the recording and attempt example problems independently to reinforce learning.
The recommendation to practice derivative calculations to transition from understanding the concept to being able to apply it effectively.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: