1.5 - The Power and Sum Difference Rules
TLDRThe video script presents a comprehensive introduction to derivative rules in calculus. It begins by defining the derivative as the limit of the difference quotient as 'h' approaches zero, which represents the slope of a tangent line at a point on a function's graph. The script then delves into various notations for derivatives, such as Lagrange's prime notation and Leibniz's dx/dy format. The core of the video focuses on simplifying the process of finding derivatives through several key rules: the constant rule, power rule, and the rules for constants multiplied by functions. The power rule is particularly highlighted for its versatility in handling functions with variables raised to a power. The script also touches on the sum and difference rules, which allow for the differentiation of functions with multiple terms. Practical examples, including the calculation of a temperature function, illustrate the application of these rules. The video concludes with a preview of more complex functions and derivative rules to be covered in subsequent lessons.
Takeaways
- 📚 The concept of a derivative is introduced as the limit of the difference quotient as h approaches zero, representing the slope of the tangent line to a function at a particular point.
- 📈 Derivative rules simplify the process of finding derivatives, especially for complex functions, building on the difference quotient definition.
- 🌐 Notation for derivatives includes Lagrange's prime notation (f'(x)) and Leibniz's notation (dy/dx), both representing the derivative of y with respect to x.
- 📉 For a constant function f(x) = c, the derivative is always zero, as a horizontal line has a slope of zero, leading to the constant rule.
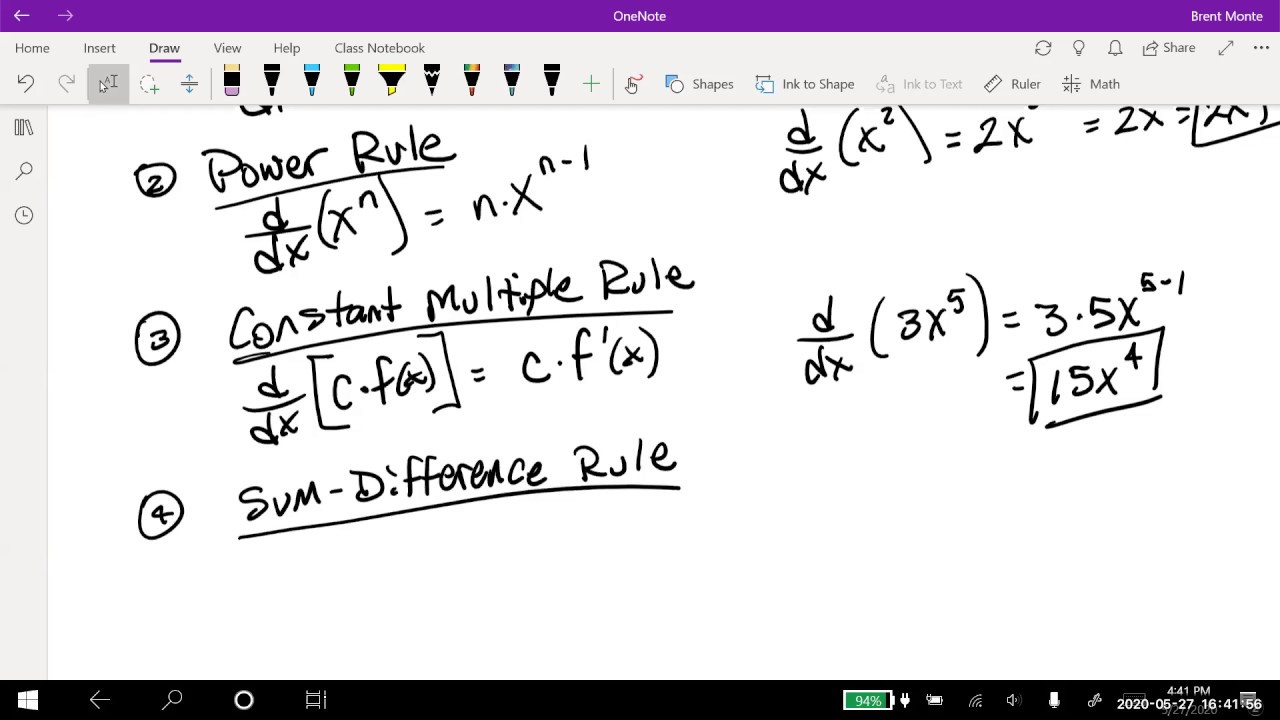
- 🎓 The power rule states that the derivative of x raised to a constant power k is k times x to the power of k minus 1, a fundamental rule for functions with exponents.
- ✅ The constant times a function rule allows us to factor out constants before differentiating the function, simplifying the process.
- 🔢 The sum and difference rules state that the derivative of a sum or difference of functions is the sum or difference of their individual derivatives, allowing term-by-term differentiation.
- 📌 The geometric interpretation of the derivative as the slope of the tangent line is crucial for understanding its application in various mathematical and real-world scenarios.
- 🤒 An example application of derivatives is in calculating the rate of change of temperature over time, demonstrating the concept's utility in modeling real-world phenomena.
- ⏱️ The instantaneous rate of change, as given by the derivative, can be contrasted with the average rate of change over an interval, highlighting the precision of derivatives in capturing change at a specific point.
- 🔧 Derivatives are not just theoretical; they can be used to find equations of tangent lines at specific points on a graph, a practical application in graphing and analyzing functions.
Q & A
What is the geometric interpretation of the derivative?
-The geometric interpretation of the derivative is that it represents the slope of the tangent line at any particular location on a function's graph.
What are the two notations commonly used to represent the derivative?
-The two notations commonly used to represent the derivative are Lagrange's notation (f'(x)) and Leibniz's notation (dy/dx).
What is the constant rule in calculus?
-The constant rule in calculus states that the derivative of a constant function is always zero, regardless of the constant's value.
How is the power rule applied to a function of the form y = x^k?
-The power rule is applied by bringing down the exponent k, making it a coefficient, and then decreasing the exponent by 1, resulting in the derivative being k * x^(k-1).
What is the significance of the difference quotient in understanding derivatives?
-The difference quotient is significant as it is the foundation for defining the derivative. It represents the limit of the ratio of the difference of the function's values as the distance between two points (h) approaches zero.
How can the derivative be used to find the equation of a tangent line at a specific point on a function's graph?
-The derivative at a specific point gives the slope of the tangent line at that point. By using the point-slope form of a line, the equation of the tangent line can be found by substituting the point's coordinates and the derivative (slope) into the formula.
What does the sum and difference rule state about differentiating functions that are added or subtracted?
-The sum and difference rule states that the derivative of a sum or difference of functions is the sum or difference of their individual derivatives. This allows for differentiation of each term independently.
How does the constant times a function rule simplify the process of differentiation?
-The constant times a function rule allows you to factor out the constant coefficient before differentiating the actual function. This simplifies the process because the constant remains unaffected by the differentiation and can be multiplied by the derivative of the function afterward.
What is the Leibniz notation for representing the derivative of y with respect to x?
-The Leibniz notation for the derivative of y with respect to x is written as dy/dx, which is read as 'the derivative of y with respect to x'.
How can negative exponents be interpreted in the context of derivatives?
-Negative exponents in derivatives are interpreted as taking the reciprocal of the base. For example, x^(-n) is the same as 1/(x^n), where n is a positive integer.
What is the process for converting a radical (root) expression into an exponential form with a fractional exponent?
-To convert a radical expression into an exponential form with a fractional exponent, you keep the base the same and use the index of the radical as the denominator of the exponent. If the base has an exponent, it becomes the numerator of the fractional exponent.
Outlines
🌟 Introduction to Derivative Rules
The video begins by introducing the concept of derivative rules, which are used to evaluate derivatives of functions more efficiently than the difference quotient, especially for complex functions. The geometric interpretation of a derivative as the slope of a tangent line is discussed, along with the importance of these rules in simplifying the process of finding derivatives.
📚 Derivative Notations and Constant Rule
The video explains different notations used to represent derivatives, such as Lagrange's prime notation (f'(x)) and Leibniz's notation (dy/dx). It also covers the constant rule, which states that the derivative of a constant function is zero, as a constant function does not change with respect to the input variable.
📈 Power Rule for Derivatives
The power rule is introduced, which allows the differentiation of functions with variables raised to a power. The rule states that the derivative of x to the power of k is k times x to the power of k minus 1. This rule is versatile and can be applied to functions with explicit or implicit exponents.
🔢 Dealing with Non-Whole Number Exponents
The video shows how to apply the power rule to functions with non-whole number exponents. It explains that the rule works the same way regardless of the exponent being a whole number, fraction, or negative number. The concept of negative exponents as reciprocals is also discussed.
🤔 Converting Radicals to Exponential Form
The video demonstrates how to convert radicals to exponential form using fractional exponents. This conversion allows the application of the power rule to functions that are not initially in the form of a variable raised to a power. The process involves rewriting roots as rational exponents and simplifying the expressions.
📝 Constant Times a Function Rule and Sum/Difference Rule
The video explains the rule for differentiating a constant times a function, which involves factoring out the constant before differentiating the function. Additionally, the sum and difference rules are introduced, which state that the derivative of a sum or difference of functions is the sum or difference of their individual derivatives. These rules allow for term-by-term differentiation of functions with multiple terms.
🧮 Applying the Rules to More Complex Functions
The video provides examples of applying the derivative rules to more complex functions, including those with multiple terms and a mix of operations. It shows how to differentiate each term individually and then combine the results according to the sum and difference rules, resulting in the overall derivative of the function.
🏥 Real-World Application: Derivatives in Temperature Analysis
The video concludes with a real-world application of derivatives, showing how to calculate the rate of change of temperature over time for a person during an illness. It demonstrates finding the general derivative of a temperature function, evaluating the derivative at a specific time to find the instantaneous rate of change, and determining the temperature at a given time point.
Mindmap
Keywords
💡Derivative
💡Difference Quotient
💡Limit
💡Tangent Line
💡Prime Notation
💡Leibniz Notation
💡Constant Rule
💡Power Rule
💡Sum and Difference Rules
💡Chain Rule
💡Instantaneous Rate of Change
Highlights
Derivatives are introduced as the limit of the difference quotient as h approaches zero, representing the slope of the tangent line at any point on a function's graph.
Derivative rules simplify the evaluation of derivatives, especially for complex functions.
Notation for derivatives includes prime notation (f'(x)), Newton notation, and Leibniz notation (d/dx).
The constant rule states that the derivative of a constant function is always zero.
The power rule allows for the differentiation of functions with variables raised to a power, expressed as k*x^(k-1).
The constant times a function rule implies that constants can be factored out before differentiating the function.
The sum and difference rules state that the derivative of a sum or difference of functions is the sum or difference of their derivatives.
Graphical interpretation of derivatives shows that for a constant function, every tangent line is horizontal with a slope of zero.
Derivatives can be evaluated at specific points to find the instantaneous rate of change at those points.
The derivative of a function at a particular point can be used to find the equation of the tangent line at that point.
The rate of change of temperature with respect to time can be found using derivatives to model real-world scenarios, such as a person's temperature during an illness.
The units of the derivative represent the rate of change, such as degrees Fahrenheit per day in the context of temperature change over time.
The difference quotient is used to develop derivative rules, which are essential for evaluating derivatives of functions with specific structures.
The power rule is versatile and can handle functions with variables raised to any constant power, including fractional powers.
Negative exponents in derivatives are handled by taking the reciprocal of the base and converting the exponent to positive.
The concept of turning points in a function's graph is related to changes in the sign of the derivative.
Derivatives can determine where a graph changes direction, indicating maximum or minimum values, known as turning points.
The derivative of a function can be used to analyze the behavior of the function, such as direction of slope change.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: