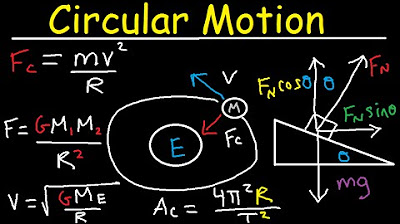
conical pendulums and banking explained

The script begins with an introduction to the topic of circular motion, building upon a previous discussion about uniform circular motion in a horizontal plane. The host outlines three more complex examples of circular motion involving centripetal forces: the conical pendulum, a banking plane, and a banked road surface. These examples are intended to deepen the understanding of concepts such as velocity, centripetal force, and their applications in real-world scenarios. The host also promises to provide timestamps in the description for viewers to navigate through different sections of the video.

This paragraph delves into the physics of the conical pendulum, a classic example of circular motion. The object is spinning in a circle with a fixed radius, influenced by two main forces: tension along the string and the weight of the object. The net force creates the centripetal force necessary for circular motion, which is mathematically described as MV^2/R. By analyzing the forces in terms of their components and using trigonometric relationships, the script derives formulas to calculate the tension in the string and the velocity of the pendulum. The host provides an example with specific values to demonstrate how to apply these formulas.

The script moves on to discuss the dynamics of a banking plane, which is an aircraft turning in a circle. The forces involved are the weight of the plane and the lift force, which combine to provide the centripetal force for the turn. Although the mathematical treatment is not detailed, it is noted to be similar to that of the conical pendulum. The host emphasizes the importance of understanding the components of force and how they contribute to the circular motion of the plane.

This section examines the physics of a car traveling on a banked road, focusing on the forces that allow the car to maintain its circular path. The normal force and the weight of the car combine to produce the centripetal force. The script explores the scenario both with and without friction, highlighting the 'ideal velocity' at which a car can travel without slipping. An example calculation is provided for a car on an icy, banked track, demonstrating how to determine the necessary speed to maintain a stable path.

The script concludes with a more complex analysis that includes friction in the circular motion equations. The forces acting on the car are broken down into vertical and horizontal components, with the net horizontal force equating to the centripetal force. The vertical forces must sum to zero since there is no vertical acceleration. The host derives a formula that incorporates friction into the calculation of the car's velocity, showing how the velocity increases with greater road friction. The script acknowledges the complexity of this scenario and encourages viewers to continue learning about the role of frictional forces in circular motion.

In an additional exploration, the script derives a formula for the period of circular motion, relating it to the velocity, radius, and the angle of inclination. The host shows that, for small angles, the period of a conical pendulum approaches that of a simple pendulum, providing a deeper understanding of the relationship between pendulum motion and circular motion. The script encourages viewers to appreciate the interconnectedness of physical concepts and to explore these connections further.