The Conical Pendulum

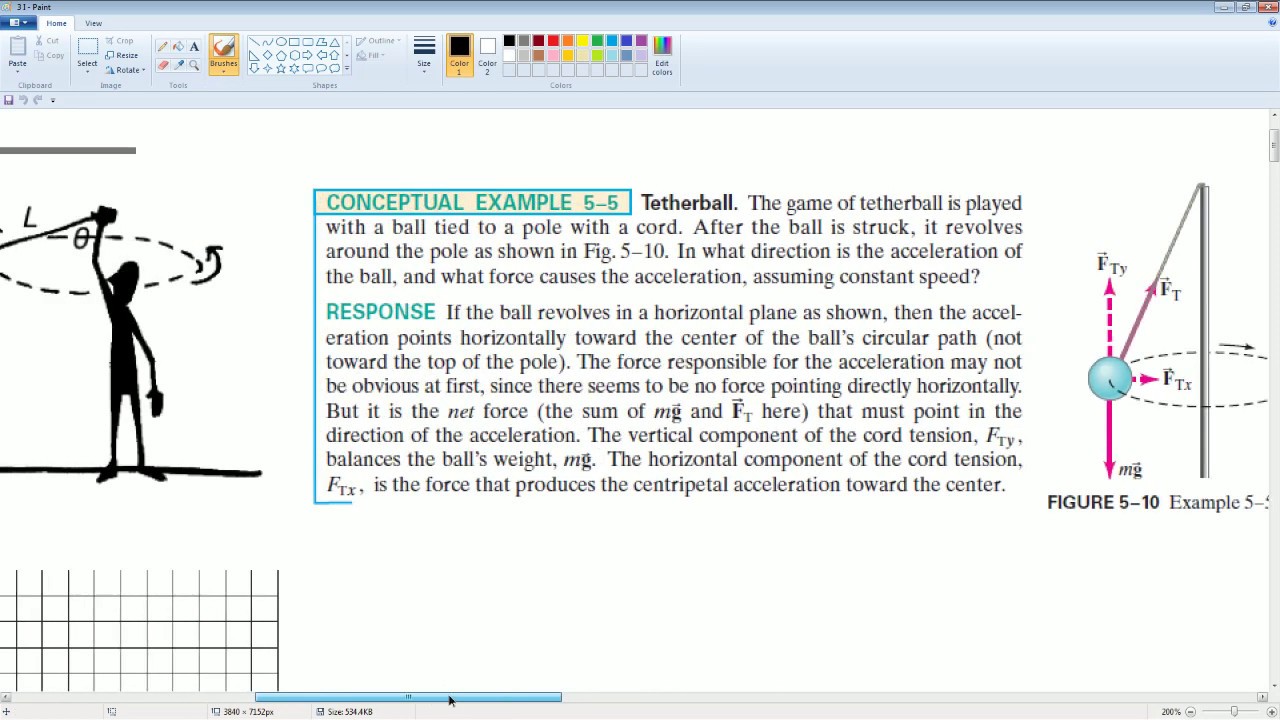
The video script begins by introducing the conical pendulum, a type of pendulum that swings in a horizontal circle due to tangential speed. It contrasts this with the simple pendulum, which swings in a circular arc. The script aims to explore the forces and circular motion involved in a conical pendulum's operation. Key variables such as the radius (R), string length, pendulum angle (theta), gravitational force (mg), and tension force (FT) are defined and diagrammed. The forces acting on the pendulum are analyzed, particularly the tension force's components in the vertical and horizontal directions, which are crucial for understanding the pendulum's motion.

This paragraph delves into applying Newton's second law to the conical pendulum in both the x and y directions. The vertical component of the tension force (fty) balances the gravitational force when there is no vertical acceleration, leading to the equation fty = mg. The horizontal component (ftx) is responsible for the centripetal force required for uniform circular motion, leading to the equation ftx = mass * centripetal acceleration. By expressing the tension force components in terms of the total tension and angle theta, two equations are derived that relate the forces to the motion characteristics of the pendulum.

The script continues by exploring the speed of the mass in a conical pendulum. By combining and simplifying the Newton's second law equations, an expression for the speed (V) of the pendulum is derived. The equation V = √(r * g * tan(theta)) shows how the speed depends on the radius of the circle, the gravitational field, and the angle theta. This relationship is discussed in the context of physical intuition, explaining how changes in radius, angle, and gravitational field strength affect the speed.

The script then discusses the use of a conical pendulum to measure the acceleration due to gravity (G). By manipulating the derived speed equation, an expression for G is obtained in terms of measurable quantities: the radius, period, and angle. The difficulty of measuring tension directly is acknowledged, and the script shows how to eliminate this variable from the equation. The resulting formula for G is simplified to G = 4 * π² * L * cos(theta) / T², where L is the string length, and T is the period of the pendulum.

The final paragraph examines the period of the conical pendulum, which is the time it takes for the pendulum to complete one full cycle. By relating the period to the speed and radius of the circle, an equation for the period is derived. The script highlights the similarity between the period equation of a conical pendulum and that of a simple pendulum, with the key difference being the inclusion of the cosine of theta in the conical pendulum's equation. This comparison provides insight into the distinct physics of conical and simple pendulums.