Centripetal Acceleration & Force - Circular Motion, Banked Curves, Static Friction, Physics Problems
TLDRThis video delves into the concepts of circular motion, centripetal force, and gravity's role in celestial bodies' orbits. It explains how forces like tension and friction contribute to centripetal force, enabling objects to move in circular paths. The video also discusses the gravitational force between bodies like the Earth and the Moon, and how it keeps the Moon in orbit. Newton's laws of motion and gravitational acceleration are applied to various scenarios, including satellites in orbit and objects in free fall, to calculate speed, period, and the effects of different forces on motion. The content is rich with examples and equations, providing a comprehensive understanding of the principles at play.
Takeaways
- 🌀 Centripetal force is required for circular motion and is perpendicular to the velocity of the object, causing a change in direction without changing the speed's magnitude.
- 📈 The magnitude of centripetal force depends on the mass of the object, the square of its velocity, and is inversely related to the radius of the circular path.
- 🔄 When velocity and force vectors are parallel, the object accelerates, while anti-parallel vectors result in deceleration.
- 🌍 Gravity provides the centripetal force necessary for celestial bodies like the Moon to orbit the Earth, and the Earth to orbit the Sun.
- 🚗 Static friction between tires and road provides the centripetal force for a car to turn safely without skidding.
- 📊 The equation for centripetal force is Fc = m*v^2/r, where Fc is the centripetal force, m is the mass, v is the velocity, and r is the radius of the circular path.
- 🔧 Tension in a string or rope can provide the centripetal force necessary to keep an object moving in a circular path, such as when swinging a ball around in a horizontal circle.
- 🪐 The gravitational force between two masses can be calculated using the equation F = G*(m1*m2)/r^2, where F is the gravitational force, G is the gravitational constant, m1 and m2 are the masses, and r is the distance between the centers of the two masses.
- 🛤️ The normal force exerted by the road on a car changes depending on whether the car is moving at a constant speed or accelerating, affecting the car's ability to make turns safely.
- 🌌 The gravitational constant (G) and the masses of celestial bodies, along with the distance between their centers, determine the gravitational force and the orbital characteristics of the bodies.
- 🚀 The acceleration due to gravity on a celestial body depends on the mass of the body and the radius of its orbit, with larger masses and smaller radii resulting in greater gravitational pull.
Q & A
What is the centripetal force and how does it affect an object moving in a circular motion?
-Centripetal force is the force that keeps an object moving in a circular path. It acts perpendicular to the velocity of the object, causing a change in direction without altering the speed. The centripetal force is necessary for circular motion and is provided by sources such as tension, gravitational force, or friction.
How does the direction of the force vector relative to the velocity vector affect the speed of an object?
-If the force vector is in the same direction as the velocity vector, the object speeds up. If they are in opposite directions, the object slows down. If they are perpendicular, the speed remains the same, but the direction changes, resulting in circular motion.
What is the formula for calculating centripetal force?
-The formula for centripetal force is Fc = mv^2/r, where Fc is the centripetal force, m is the mass of the object, v is the velocity, and r is the radius of the circular path.
How does the mass, velocity, and radius of circular motion affect the magnitude of centripetal force?
-The centripetal force is directly proportional to the mass and the square of the velocity, and inversely proportional to the radius. Increasing the mass or velocity increases the force, while increasing the radius decreases it.
What is the role of gravity in the motion of celestial bodies like the Earth and the Moon?
-Gravity provides the necessary centripetal force that keeps celestial bodies like the Earth and the Moon in their orbits. The gravitational force between two masses pulls them towards each other, allowing them to move in circular orbits around their common center of mass.
How does Newton's law of gravitation relate to centripetal force in satellite motion?
-Newton's law of gravitation states that every point mass attracts every other point mass by a force acting along the line intersecting both points. This force is proportional to the product of the two masses and inversely proportional to the square of the distance between them. In satellite motion, this gravitational force acts as the centripetal force that keeps the satellite in orbit around a planet.
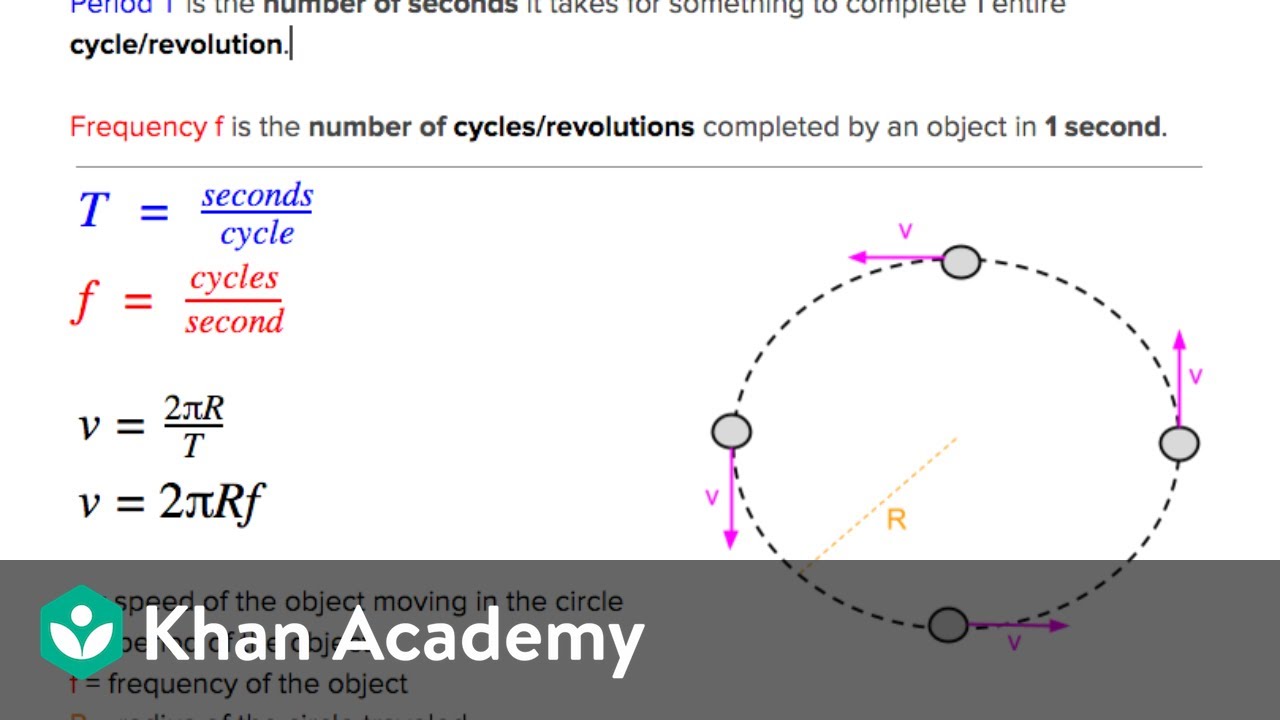
What is the relationship between the period and frequency of circular motion?
-The period is the time taken for one complete revolution, while the frequency is the number of revolutions per unit time. They are inversely related, with the period being the reciprocal of the frequency (T = 1/f).
How can you calculate the speed of an object moving in a circular path given the radius and period?
-The speed (v) of an object moving in a circular path can be calculated using the formula v = 2πr/T, where r is the radius of the path and T is the period of motion.
What is the difference between centripetal force and centripetal acceleration?
-Centripetal force is the net force acting on an object to keep it moving in a circular path, while centripetal acceleration is the rate of change of velocity directed towards the center of the circular path. The centripetal force causes the centripetal acceleration.
How does the tension in a string affect the centripetal force when a ball is swung in a horizontal circle?
-The tension in the string provides the necessary centripetal force to keep the ball moving in a horizontal circle. The tension must be sufficient to overcome the weight of the ball and provide the inward force needed for circular motion. At high speeds, the tension is approximately equal to the centripetal force, but at low speeds, the tension must also support the weight of the ball.
What is the minimum speed required for an object to maintain contact with a circular path without falling out?
-The minimum speed required for an object to maintain contact with a circular path is when the normal force is equal to the weight of the object. This speed can be calculated using the formula v = √(g*r), where g is the gravitational acceleration and r is the radius of the circular path.
Outlines
🌀 Introduction to Circular Motion Concepts
This paragraph introduces the fundamental concepts of circular motion, including centripetal force, tension, satellite motion, Newton's law of gravitation, and the role of gravity. It explains how the direction of force and velocity vectors affects an object's speed and the circular path it takes when the force is perpendicular to the velocity. Various examples, such as a ball on a string and the Earth-Moon gravitational interaction, are used to illustrate these principles.
🚗 Centripetal Force in Real-World Scenarios
The paragraph discusses the application of centripetal force in everyday scenarios, like a car turning on a road, where friction provides the necessary centripetal force. It also touches on the concept of gravitational force keeping the Moon in orbit around the Earth. The paragraph further explains how different forces, such as tension and normal force, can provide centripetal force in various situations, including the magnetic force on a moving charge.
📝 Equations of Centripetal Force and Acceleration
This section presents the mathematical equations governing centripetal force and acceleration. The formula for centripetal force (Fc = mv^2/r) is derived, and its dependence on mass, velocity, and radius is discussed. The relationship between centripetal acceleration (ac = v^2/r) and the force is explained. The paragraph also demonstrates how changes in mass, velocity, and radius affect the magnitude of centripetal force and acceleration.
📊 Analysis of Circular Motion Parameters
The paragraph delves into the calculation of circular motion parameters such as frequency, period, speed, and centripetal acceleration. It explains the relationship between these parameters and provides equations for calculating them. The concept of centripetal acceleration always pointing towards the center of the circle is highlighted. The paragraph also includes a practice problem involving a ball moving in a circle with given radius, frequency, and period to calculate various motion parameters.
🛫 Centripetal Acceleration in G-Forces
This section discusses the concept of G-forces in relation to centripetal acceleration. It explains how to convert centripetal acceleration into G-forces and vice versa. The paragraph presents a problem involving a plane making a circular turn and calculates the corresponding centripetal acceleration in G-forces. The principles of unit conversion are also explained in the context of this calculation.
🌐 Tension Force in Horizontal and Vertical Circles
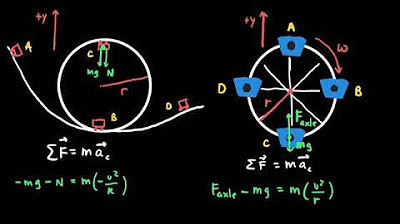
The paragraph explores the calculation of tension force when an object is moving in both horizontal and vertical circles. It explains the difference in tension force at various points in the circle, such as at the top, bottom, and sides, and how the tension force relates to the centripetal force. The paragraph includes detailed calculations for a ball moving in a horizontal circle and a ball swinging in a vertical circle, taking into account the weight force and the required centripetal force.
🏎️ Minimum Speed for Circular Motion without Friction
This section discusses the minimum speed required for an object to maintain circular motion without the need for frictional force. It explains the concept of setting the tension force equal to zero to find the threshold speed for horizontal and vertical circular motion. The paragraph presents calculations for finding the minimum speed for a ball tied to a string moving in a vertical circle and the maximum speed for a car to safely navigate a circular turn without skidding.
🚀 Geosynchronous Satellites and Kepler's Laws
The paragraph focuses on geosynchronous satellites, which maintain a fixed position relative to the Earth's surface. It explains how to calculate the height and speed of such satellites using the period of Earth's rotation. The concept of gravitational force providing the necessary centripetal force for satellite orbit is discussed. The paragraph also covers Kepler's laws of planetary motion, particularly the third law, which relates the periods and distances of planets from the Sun, and uses these laws to calculate the orbital period of Mars and the distance of Mercury from the Sun.
📈 Gravitational Force and Acceleration
This section quantifies the force of gravity using the universal law of gravitation formula (F = G * (m1 * m2) / r^2), where G is the gravitational constant, m1 and m2 are the masses of the objects, and r is the distance between their centers. The gravitational force between the Earth and the Sun is calculated using their masses and the distance between them. The effects of changing the mass of the Earth or the distance between the Earth and the Sun on the gravitational force are discussed. The paragraph also calculates the acceleration due to gravity at the surface of the Earth and the Moon, and at a point above Earth's surface.
🛰️ Satellite Orbits and Speed Calculation
The paragraph explains how to calculate the speed and orbital period of a satellite in a circular orbit above Earth's surface. It uses the gravitational force as the centripetal force required to keep the satellite in orbit. The speed of a satellite is determined by the gravitational constant, the mass of the Earth, and the distance between the satellite and Earth's center. The period of the satellite is calculated using the speed and the orbital radius. The concept is applied to find the speed and period of a satellite 3,000 kilometers above Earth's surface.
🌍 Earth-Sun Mass Ratio and Kepler's Third Law
This section uses Kepler's third law to calculate the mass of the Sun based on the Earth's orbital period and distance from the Sun. The law states that the square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit. By comparing the Earth's orbit to that of Mars and Mercury, the period of Mars and the distance of Mercury from the Sun are calculated. The process involves solving a system of equations derived from Kepler's law, which requires understanding the relationship between the orbital periods and distances of celestial bodies.
🏢 Elevator Physics: Weight and Acceleration
The paragraph discusses the physics of being in an elevator, focusing on how the scale reads different forces depending on the elevator's motion. When the elevator is at rest or moving at a constant velocity, the scale reads the person's weight (mg). However, when the elevator accelerates upward or downward, the normal force changes, and the scale reads a different value. The paragraph explains the calculations for the normal force and the scale readings during upward and downward acceleration, highlighting the relationship between force, mass, and acceleration in the context of an elevator.
Mindmap
Keywords
💡Circular Motion
💡Centripetal Force
💡Tension
💡Satellite Motion
💡Newton's Law of Gravitation
💡Velocity Vector
💡Force Vector
💡Gravitational Force
💡Static Friction
💡Magnetic Force
Highlights
Explained the concept of circular motion, including centripetal force and its role in maintaining an object's circular path.
Described how the direction of force relative to velocity affects an object's speed, including acceleration and deceleration scenarios.
Detailed the relationship between force, velocity, and direction in circular motion, emphasizing the perpendicular nature of centripetal force.
Explained the role of tension in providing centripetal force, using the example of a ball on a string moving in a circle.
Discussed the gravitational force between celestial bodies, like the Earth and the Moon, and how gravity acts as a centripetal force in orbital motion.
Introduced Newton's law of gravitation and its application in calculating the gravitational force between two masses.
Explained how different forces (tension, friction, magnetic) can provide the necessary centripetal force for circular motion.
Provided the formula for centripetal force (Fc = mv^2/r) and discussed its dependence on mass, velocity, and radius.
Explained how changes in mass, velocity, and radius impact the magnitude of centripetal force, using mathematical examples.
Described the concept of centripetal acceleration and its directionality, always pointing towards the center of the circular path.
Related the frequency and period of an object's circular motion to its speed, providing the formula for calculating speed in such motion.
Presented a practical problem involving a ball moving in a circular path, demonstrating the application of centripetal force and acceleration formulas.
Discussed the calculation of tension force in a rope when a ball moves in a horizontal circle, incorporating both centripetal force and weight.
Explained the concept of geosynchronous satellites and how their period matches the Earth's rotation, with a focus on their height and speed.
Applied Newton's second law to discuss the net force, centripetal acceleration, and tension force when an object moves in a vertical circle.
Introduced the concept of gravitational acceleration and how it varies with the mass of the celestial body and its radius.
Calculated the gravitational force between the Earth and the Sun, demonstrating the application of the universal gravitation formula.
Discussed the impact of changing the mass of celestial bodies and the distance between them on the gravitational force.
Transcripts
Browse More Related Video

Centripetal force and acceleration intuition | Physics | Khan Academy
AP Physics 1 Circular Motion and Gravitation Review
AP Physics 1 review of Centripetal Forces | Physics | Khan Academy

What Is Circular Motion? | Physics in Motion

What is Centripetal force?

2022 Live Review 3 | AP Physics 1 | Understanding Circular Motion and Gravitation
5.0 / 5 (0 votes)
Thanks for rating: