banked curves and circular motion explained
TLDRIn this educational video, Paul from Physics High succinctly explains the physics behind banked curves, a concept where roads are angled to allow vehicles to travel faster around a curve. He demonstrates how the centripetal force, resulting from the car's weight (mg) and the normal force, keeps the car in circular motion. By simplifying the scenario without friction, Paul uses vector analysis and component analysis to derive the formula for the velocity (V) of an object in circular motion, which is independent of mass and depends on the radius (r) and angle (Theta) of the banked curve. The video also touches on the complexity added by friction and encourages viewers to watch a more detailed video for further understanding.
Takeaways
- 🚗 The video discusses forces involved with banked curves, which are curved tracks designed to allow vehicles to travel faster around turns.
- 🎥 Paul, from Physics High, is the presenter who provides an overview of banked curves and their physics.
- 🔗 A more detailed video on banked curves is available, which this short version complements.
- 📐 Banked curves are circular tracks with the road surface at an angle to increase speed around the curve.
- 🧲 The primary forces considered in the analysis are gravity (mg) and the normal force, with friction being ignored for simplicity.
- 📚 The relationship between the forces is visualized through vector diagrams and component analysis.
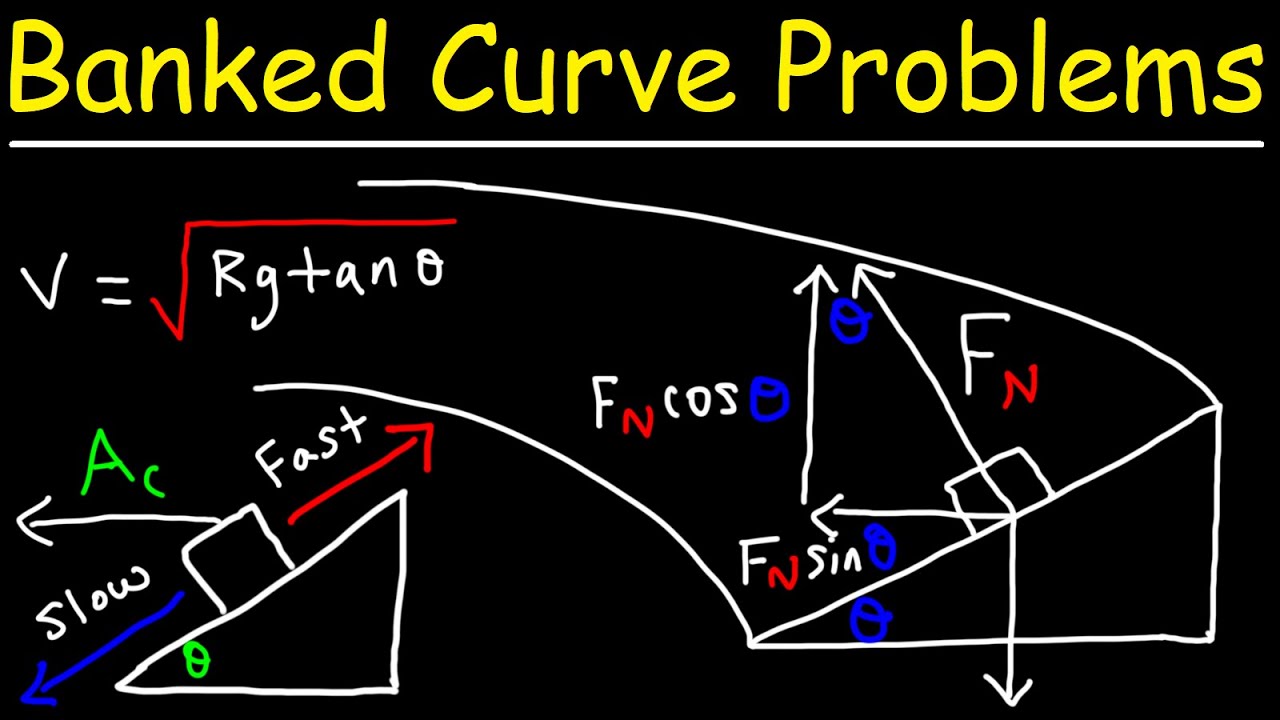
- 📉 The centripetal force, which keeps the car in circular motion, is the resultant of the normal force and gravitational force.
- 🔍 The tangent of the angle theta (θ) is equal to the ratio of centripetal force (Mv^2/r) to the gravitational force (mg).
- 📘 The formula derived for velocity (V) is V = √(g * r * tan(θ)), showing that it is independent of the car's mass.
- 🔄 If the velocity increases, the car will move up the bank; if it decreases, it will move down, indicating the role of velocity in maintaining circular motion.
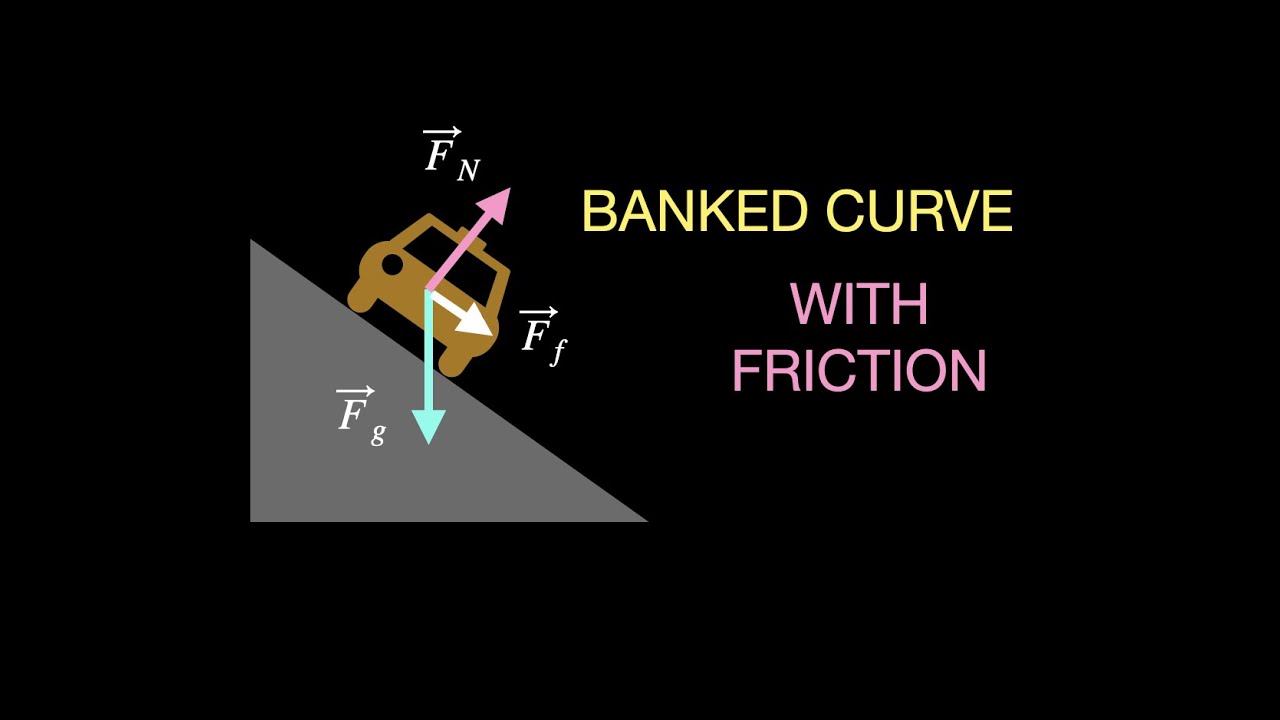
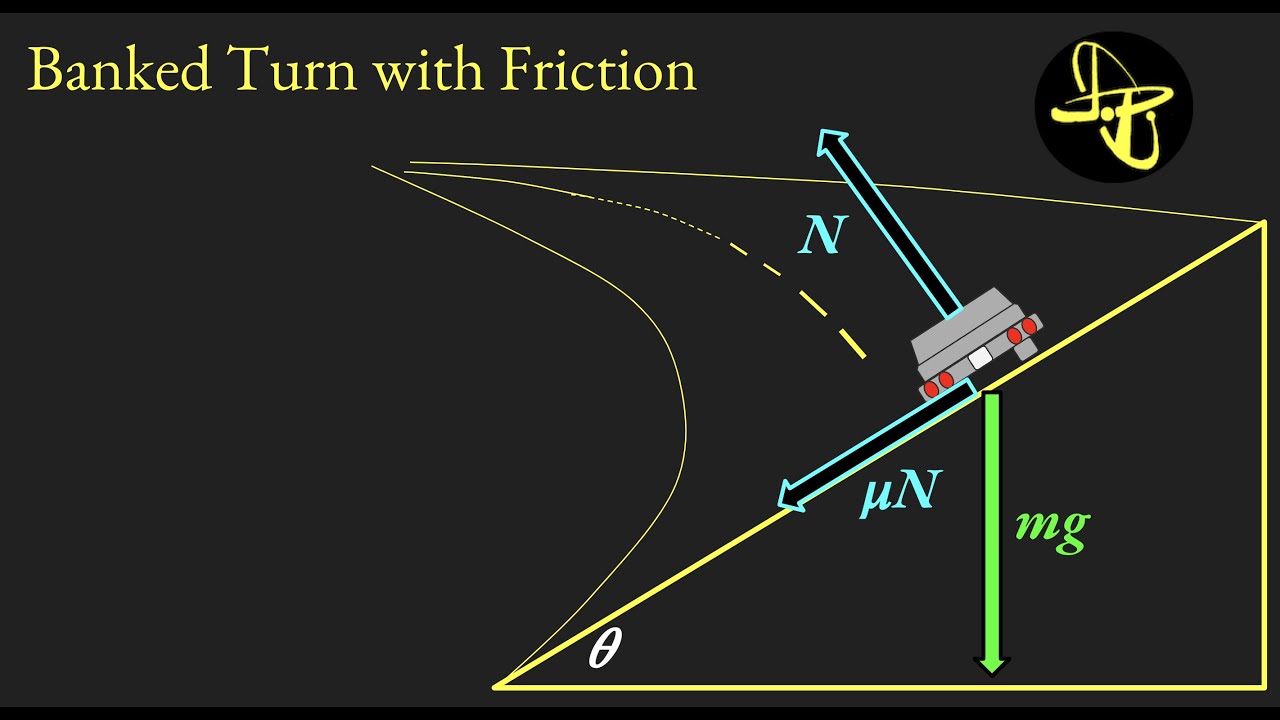
- 🚫 Adding friction to the analysis complicates the scenario, which is typically not required in high school exams but is covered in more detail in the full video.
Q & A
What is a banked curve in the context of physics?
-A banked curve is a circular track designed for vehicles to travel around at higher speeds. The road surface is angled to increase the opportunity for faster travel around the curve.
What is the purpose of banking a curve on a track?
-Banking a curve on a track is done to increase the speed at which a vehicle can safely navigate the curve, by providing additional centripetal force through the angle of the bank.
What are the two basic forces considered in the analysis of banked curves without friction?
-The two basic forces considered are the force due to the weight of the car (mg) and the normal force acting perpendicular to the road surface.
How does the centripetal force in a banked curve scenario relate to the forces of weight and normal force?
-The centripetal force in a banked curve scenario is the result of the weight force and the normal force acting together. It is the net force that keeps the car moving in a circular path.
What mathematical relationship can be derived from the forces acting on a car in a banked curve?
-The mathematical relationship derived is that the tangent of the angle of the bank (theta) is equal to the centripetal force (which is MV^2/r) divided by the weight force (mg). Simplifying this gives V^2 = g*r*tan(theta), where V is the velocity of the car.
Why is the mass of the car not included in the formula for the velocity required to stay in circular motion on a banked curve?
-The mass of the car is not included in the formula because the velocity required for an object to stay in circular motion on a banked curve is independent of its mass, given that friction is ignored.
What happens to the car if the velocity increases or decreases on a banked curve?
-If the velocity increases, the car will slide up the hill due to the increased normal force. If the velocity decreases, the car will slide down the hill due to the reduced normal force.
What is vector analysis and how is it used in the context of banked curves?
-Vector analysis is a method of breaking down forces into their component parts. In the context of banked curves, it is used to determine the relationship between the normal force, weight, and centripetal force acting on a car.
What is component analysis and how does it relate to the normal force in a banked curve scenario?
-Component analysis is a technique used to resolve vectors into their orthogonal components. In a banked curve scenario, it is used to separate the normal force into horizontal and vertical components, where the horizontal component provides the centripetal force.
What additional complexity is introduced when friction is considered in the analysis of banked curves?
-When friction is considered, the analysis becomes more complex as it introduces an additional vector force that must be added to the component analysis. The frictional force is equal to the coefficient of friction (mu) times the normal force and can act either up or down the plane.
What is the significance of the angle theta in the context of banked curves?
-Theta is the angle of the banked curve. It is significant because it determines the relationship between the normal force, weight, and the required centripetal force for a car to maintain circular motion without sliding.
Outlines
🚗 Introduction to Banked Curves and Forces
Paul from Physics High introduces the concept of banked curves, explaining the forces involved when a car navigates a circular track. He simplifies the scenario by ignoring frictional forces to focus on the primary forces: the car's weight (mg) and the normal force from the road. He illustrates how these forces combine to create the centripetal force necessary for circular motion. Paul uses both vector analysis and component analysis to derive the formula for the velocity of an object in circular motion on a banked curve, which is independent of the object's mass. The formula is V = √(g * r * tan(θ)), where g is the acceleration due to gravity, r is the radius of the curve, and θ is the angle of the banked curve.
🔍 Adding Friction to Banked Curve Analysis
In the second paragraph, Paul touches on the complexity added when friction is considered in the analysis of banked curves. He mentions that frictional force can act in two different scenarios, either up or down the plane, leading to two distinct cases to explore. The frictional force is described as being equal to the coefficient of friction (μ) times the normal force. Although not detailed in this short version of the video, Paul refers viewers to a more comprehensive video where he explains how to include friction in the component analysis of banked curves. He concludes by hoping the explanation aids in understanding banked curves and signs off with a reminder of his affiliation with Physics High.
Mindmap
Keywords
💡Banked curves
💡Centripetal force
💡Normal force
💡Gravitational force
💡Frictional forces
💡Vector analysis
💡Component analysis
💡Tangential
💡Velocity
💡Mass
Highlights
Introduction to banked curves and their purpose in allowing vehicles to travel faster around curves.
Explanation of centripetal force resulting in a car's circular motion on a banked curve.
Simplification of the problem by ignoring frictional forces for the initial analysis.
Identification of two basic forces acting on a car: weight (mg) and normal force.
Vector diagram used to combine the forces acting on the car.
Mathematical relationship derived from the forces: tan(theta) = centripetal force / mg.
Velocity formula for an object in circular motion: V = sqrt((g * r * tan(theta)) / r).
Independence of mass in the formula for velocity in banked curves.
Behavior of the car with changes in velocity: sliding up or down the hill.
Introduction to component analysis of forces.
Breaking down the normal force into vertical and horizontal components.
Derivation of the centripetal force from the horizontal component of the normal force.
Vertical component of the normal force balancing the weight of the car.
Component analysis leading to the same velocity formula as vector analysis.
Complexity introduced by adding friction to the analysis.
Mention of frictional force direction and its impact on the analysis.
Brief mention of a more detailed video on banked curves with friction.
Conclusion and sign-off by Paul from Physics High.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: