What is inferential statistics? Explained in 6 simple Steps.
TLDRThis video offers an insightful exploration of inferential statistics, detailing its purpose and methodology. It defines key concepts such as population and sample, and outlines the six-step process for making inferences about a population using sample data. The video explains hypothesis testing, the significance of P-values, and the concept of statistical significance, including the potential for type one and type two errors. It concludes with a practical guide on selecting the appropriate hypothesis test using an online tool, ensuring viewers can apply these concepts to real-world data analysis.
Takeaways
- 🔍 Inferential statistics is a method to make conclusions about a population based on data from a sample.
- 🌐 The 'population' is the entire group of interest, while a 'sample' is a smaller subset of the population that is actually studied.
- 💡 The process starts with a hypothesis, which is a statement that we want to test for evidence.
- 🧐 Hypothesis testing involves comparing a research hypothesis (alternative hypothesis) with a null hypothesis, which assumes no effect or difference.
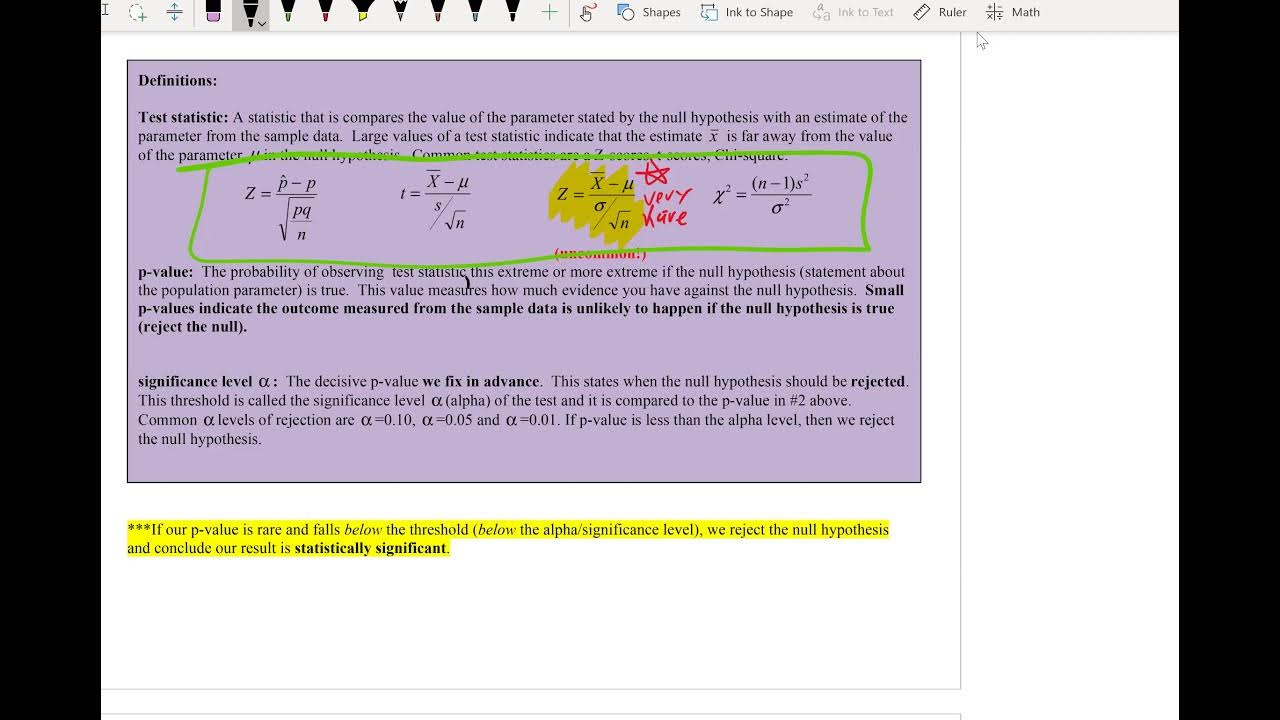
- 📉 The null hypothesis is tested by assuming it's true and calculating the probability (P value) of observing the sample data or more extreme data.
- 📍 A P value indicates the probability of getting a sample that deviates as much or more than the observed sample, assuming the null hypothesis is true.
- ✅ Statistical significance is often determined by a P value threshold, commonly set at 0.05, below which the result is considered unlikely to be due to chance.
- 🚫 There is always a risk of making an error in hypothesis testing, known as Type I (rejecting a true null hypothesis) or Type II (failing to reject a false null hypothesis).
- 🛠 Data analysis tools can assist in finding a suitable hypothesis test, calculating it, and interpreting the results.
- 📚 Understanding the difference between parametric and nonparametric tests is important for selecting the right hypothesis test.
- 🔑 The video offers guidance on how to find the right test and interpret results using a tool like data.net.
Q & A
What is inferential statistics and what does it allow us to do?
-Inferential statistics is a set of statistical methods that allows us to make conclusions or inferences about a population based on the data from a sample. It enables us to draw insights about the entire group of interest by studying a smaller, more manageable subset of that group.
What is meant by 'population' in the context of inferential statistics?
-In inferential statistics, the 'population' refers to the entire group that we are interested in studying. For example, if we are interested in the heights of all adults in the United States, then the population would be all adults in the United States.
Can you define 'sample' in relation to inferential statistics?
-A 'sample' is a smaller group chosen from the population that we actually study. It is used to represent the larger population and to make inferences about it. For instance, if we select 150 adults from the United States, that group of 150 would be our sample.
What is the purpose of a hypothesis in inferential statistics?
-A hypothesis in inferential statistics is a statement that we want to test. It is a proposed explanation for a phenomenon, which we investigate by collecting and analyzing data. For example, we might hypothesize that a drug has a positive effect on blood pressure in people with high blood pressure.
What is a null hypothesis and why is it used?
-The null hypothesis is a statement that there is no effect or no difference in the population. It is used as a starting point in hypothesis testing. We assume that the null hypothesis is true and then gather data to see if the sample evidence contradicts this assumption. If the data is unlikely under the null hypothesis, we may reject it in favor of the alternative hypothesis.
Can you explain the concept of hypothesis testing?
-Hypothesis testing is a method for testing a claim about a parameter in a population using data measured in a sample. It involves setting up a null hypothesis, calculating how much the sample deviates from this hypothesis, and determining a P-value to assess the probability of observing such a deviation if the null hypothesis were true.
What is a P-value and what does it indicate?
-A P-value is the probability of getting a sample that deviates as much or more than our observed sample, assuming that the null hypothesis is true. It indicates how likely it is to observe the data (or something more extreme) if the null hypothesis were true. A small P-value suggests that the observed data is inconsistent with the null hypothesis, leading to its rejection.
What is the significance of a P-value being less than 0.05 in hypothesis testing?
-If the P-value is less than a predetermined threshold, often 0.05, the result is considered statistically significant. This means that the observed effect is unlikely to have occurred by chance alone, providing enough evidence to reject the null hypothesis in favor of the alternative hypothesis.
What are type one and type two errors in the context of hypothesis testing?
-Type one error occurs when a true null hypothesis is rejected, meaning we mistakenly believe an effect exists when it does not. Type two error occurs when a false null hypothesis is not rejected, meaning we mistakenly believe no effect exists when there actually is one.
How does the video suggest finding a suitable hypothesis test for a given data set?
-The video suggests using a tool like data.net, where you can input your data into a table. The platform will then suggest a hypothesis test based on the variables and data provided, such as a Chi-Square test or an analysis of variance (ANOVA).
What is the difference between parametric and nonparametric tests as mentioned in the video?
-The video does not provide a detailed explanation of the difference between parametric and nonparametric tests. However, generally, parametric tests assume that the data follows a specific distribution (like normal distribution) and have parameters that can be estimated, while nonparametric tests do not make such assumptions and are often used when the data does not meet the assumptions required for parametric tests.
Outlines
📊 Introduction to Inferential Statistics
This paragraph introduces the concept of inferential statistics, which is the process of making conclusions about a population based on data from a sample. It explains the distinction between a population (the entire group of interest, such as all adults in the United States) and a sample (a smaller subset of the population, like 150 adults). The paragraph outlines the six key steps involved in making inferences, starting with formulating a hypothesis. The hypothesis is a statement that we want to test, such as whether a drug affects blood pressure in people with high blood pressure. The paragraph also introduces the concept of hypothesis testing, which is a method for evaluating claims about a population parameter using sample data. It sets the stage for further explanation of hypothesis testing, P-values, and statistical significance.
🔍 Hypothesis Testing and Errors in Statistics
This paragraph delves into the mechanics of hypothesis testing, starting with the null hypothesis, which assumes no effect or difference in the population. It contrasts this with the alternative hypothesis, which we are trying to support with evidence. The paragraph explains that a hypothesis test involves calculating how much the sample deviates from the null hypothesis and using the P-value to determine the probability of observing such a deviation if the null hypothesis were true. A P-value less than a predetermined threshold (often 0.05) indicates statistical significance, suggesting that the observed data is inconsistent with the null hypothesis, leading to its rejection in favor of the alternative. The paragraph also discusses the risks of making errors in hypothesis testing, known as Type I and Type II errors, where a Type I error occurs when the true null hypothesis is rejected, and a Type II error occurs when a false null hypothesis is not rejected. The paragraph concludes with a brief mention of how Data.net can assist in finding a suitable hypothesis test, calculating it, and interpreting the results.
Mindmap
Keywords
💡Inferential Statistics
💡Population
💡Sample
💡Hypothesis
💡Hypothesis Testing
💡Null Hypothesis
💡P-Value
💡Statistical Significance
💡Type I Error
💡Type II Error
💡Parametric vs. Nonparametric Tests
Highlights
Inferential statistics allows making conclusions about a population based on sample data.
The population is the entire group of interest, and the sample is a smaller group selected from it.
Six key components are explained to understand how to make statements about a population using a sample.
A hypothesis is a statement to be tested, such as the effect of a drug on blood pressure.
Hypothesis testing is a method for testing claims about a population parameter using sample data.
A research hypothesis, or alternative hypothesis, is what we seek evidence for.
The null hypothesis states there is no effect or difference in the population.
The P-value indicates the probability of observing the sample result assuming the null hypothesis is true.
A P-value less than 0.05 is often considered statistically significant, leading to the rejection of the null hypothesis.
Statistical significance means the result is unlikely due to chance, providing evidence to reject the null hypothesis.
A large P-value suggests the observed data is consistent with the null hypothesis, and it is not rejected.
Errors in hypothesis testing include type one (rejecting a true null hypothesis) and type two (failing to reject a false null hypothesis).
A small P-value does not prove the alternative hypothesis is true, only that it is unlikely under the null hypothesis.
Data helps in finding a suitable hypothesis test, calculating it, and interpreting the results.
Data.net is a tool that can suggest a hypothesis test based on the variables and data provided.
Parametric and non-parametric tests are distinguished, with explanations available in subsequent videos.
The video concludes with a guide to help viewers understand the process of hypothesis testing and its significance.
Transcripts
Browse More Related Video

Hypothesis testing: step-by-step, p-value, t-test for difference of two means - Statistics Help

Null Hypothesis, p-Value, Statistical Significance, Type 1 Error and Type 2 Error

AP Statistics Unit 6 Summary Review Inference for Proportions Part 2 Significance Tests

How P-Values Help Us Test Hypotheses: Crash Course Statistics #21
Math 119 Chap 8 part 1

p-Value (Statistics made simple)
5.0 / 5 (0 votes)
Thanks for rating: