Hypothesis testing: step-by-step, p-value, t-test for difference of two means - Statistics Help

Dr Nic's Maths and Stats

5 Dec 201107:38

EducationalLearning

32 Likes 10 Comments

TLDRThis video script offers a comprehensive guide to hypothesis testing, a fundamental procedure in inferential statistics. It outlines the five key steps: formulating null (H0) and alternative (H1) hypotheses, determining the significance level (alpha), sampling from the population, calculating the p-value, and making a decision based on the p-value. The script uses an engaging example involving Helen's choconutties sales to illustrate the process. It explains the concepts of two-tailed and one-tailed tests, and emphasizes the importance of using sample data to infer population parameters. The example concludes with a decision to reject the null hypothesis based on a p-value less than the chosen significance level, indicating a significant difference in sales when a free sticker is offered. The script encourages viewers to further explore understanding the p-value and conducting two-means tests in Excel.

Takeaways

🔍 **Hypothesis Testing Overview**: Hypothesis testing is a statistical method to make inferences about a population from a sample.
⚖️ **Setting Up Hypotheses**: Establish a null hypothesis (H0) and an alternative hypothesis (H1 or Ha), where H0 represents the status quo and H1 what you're trying to prove.
📊 **Significance Level**: Choose a significance level, commonly 0.05 or alpha, which is the probability of a type 1 error—incorrectly rejecting a true null hypothesis.
🎯 **Sample Selection**: Take a sample from the population to gather data for statistical analysis.
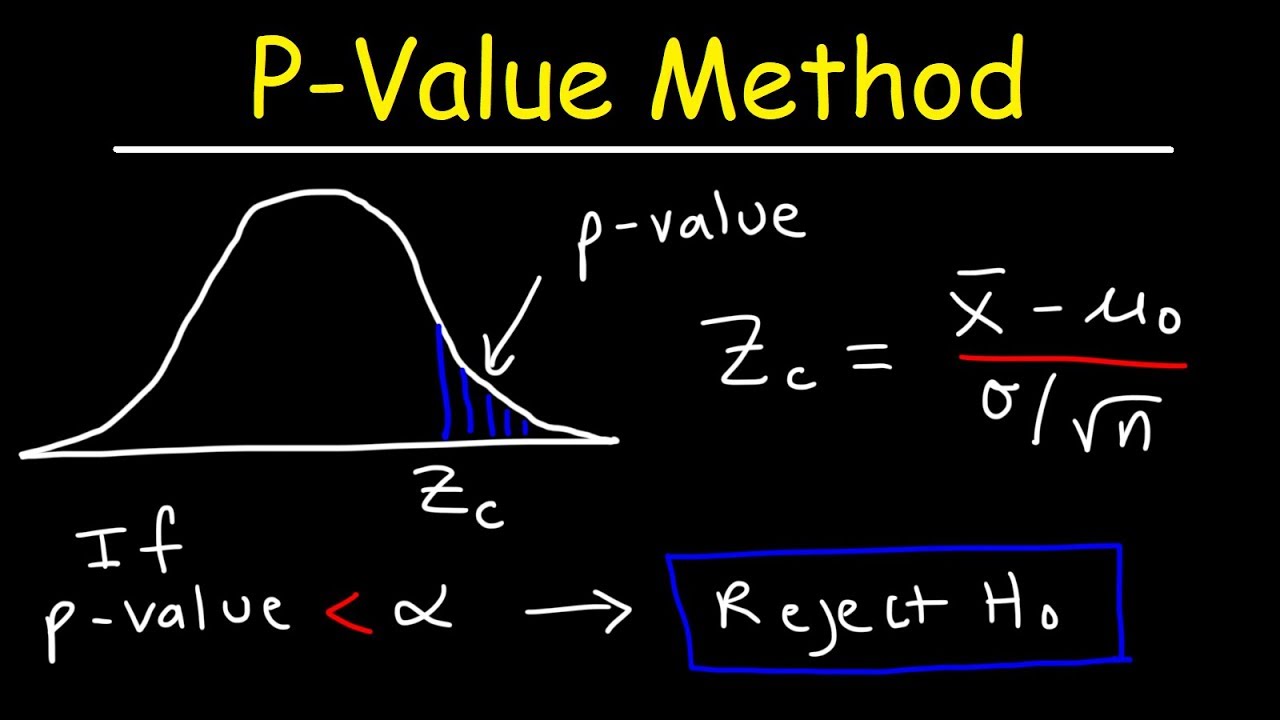
🧮 **P-Value Calculation**: Calculate the p-value using statistical software, which will be used to determine the validity of the null hypothesis.
✅ **Decision Making**: If the p-value is less than the chosen significance level, reject the null hypothesis; otherwise, do not reject it.
📚 **Example Scenario**: Helen's choconutties sales experiment is used to illustrate hypothesis testing steps, including setting up hypotheses, significance level, and analyzing sales data.
🧲 **Randomization in Sampling**: To ensure a fair test, Helen randomizes the offering of free stickers by flipping a coin each day.
📈 **Mean Sales as a Statistic**: The mean or average value of daily sales serves as the statistic of interest in Helen's experiment.
📉 **Null vs. Alternative Hypothesis**: The null hypothesis states no difference in sales between treatments, while the alternative suggests a difference.
📝 **Two-Tailed vs. One-Tailed Test**: A two-tailed test considers differences in both directions, whereas a one-tailed test focuses on a specific direction (e.g., sales increase).
📊 **Data Analysis Tools**: Use tools like Excel for data visualization and p-value calculation, as demonstrated in the 'Two means t-test in Excel' video.

Q & A

What is the fundamental concept behind hypothesis testing in inferential statistics?
-Hypothesis testing is based on the idea that we can make inferences about a population from a sample taken from it. It allows us to test whether there is evidence to support or refute a claim about the population parameters.
What are the two types of hypotheses typically established in hypothesis testing?
-The two types of hypotheses are the null hypothesis (H0), which represents the status quo or no effect, and the alternative hypothesis (H1 or Ha), which is what we are trying to provide evidence for and is the opposite of the null hypothesis.
What is the significance level in hypothesis testing, and why is it important?
-The significance level, often denoted as alpha (α), is the probability of rejecting the null hypothesis when it is actually true, also known as a type I error. It is important because it sets the threshold for deciding whether the evidence is strong enough to reject the null hypothesis.
What is a p-value in the context of hypothesis testing, and how is it used?
-The p-value is the probability of observing a test statistic as extreme as, or more extreme than, the one calculated from the sample data, under the assumption that the null hypothesis is true. It is used to decide whether to reject the null hypothesis; if the p-value is less than the chosen significance level, the null hypothesis is rejected.
How does the example of Helen and her Choco-nutties illustrate the application of hypothesis testing?
-Helen's example demonstrates hypothesis testing through a real-world scenario. She sets up null and alternative hypotheses regarding the effect of offering a free sticker on sales. She then collects data, calculates the p-value, and uses it to decide whether to reject the null hypothesis, thus determining if offering a free sticker impacts sales.
What is the difference between a one-tailed and a two-tailed test in hypothesis testing?
-A one-tailed test is used when the alternative hypothesis predicts a change in a specific direction (e.g., sales will increase). A two-tailed test, on the other hand, is used when the alternative hypothesis predicts a change in either direction (e.g., sales will increase or decrease). The choice between one-tailed and two-tailed tests depends on the nature of the research question.
Why is it important to use a random process, such as flipping a coin, in Helen's experiment?
-Using a random process ensures that the assignment of the treatment (offering a free sticker or not) is not biased. This randomness helps to eliminate other factors that might affect the results and allows for a more accurate assessment of the impact of the treatment on sales.
What does it mean to reject the null hypothesis in the context of Helen's sales data?
-Rejecting the null hypothesis in Helen's case means that the data provides evidence to suggest that there is a statistically significant difference in mean sales between days when a free sticker is offered and days when it is not, based on the chosen significance level.
How does the sample mean differ from the population mean in hypothesis testing?
-The sample mean is the average value calculated from the data collected in the sample, while the population mean is the average value for the entire population. Hypothesis testing uses the sample mean to make inferences about the population mean, under the assumption that the sample is representative of the population.
What is the role of Excel or other statistical software in calculating the p-value in hypothesis testing?
-Excel or other statistical software is used to perform the necessary calculations, including the computation of the p-value. These tools can handle complex statistical formulas and large datasets efficiently, providing a more accurate and less time-consuming way to analyze the results of a hypothesis test.
What is the implication of the p-value being less than 0.05 in Helen's experiment?
-If the p-value is less than 0.05, it indicates that there is less than a 5% probability that the observed difference in sales is due to chance alone. This leads to the rejection of the null hypothesis, suggesting that offering a free sticker has a statistically significant effect on the mean sales.

Outlines

00:00

🔍 Hypothesis Testing Explained

This paragraph introduces the concept of hypothesis testing in inferential statistics, emphasizing its five critical steps: establishing hypotheses (null and alternative), determining significance level, sampling, calculating the p-value, and making a decision based on the p-value. It highlights that the goal is to disprove the null hypothesis, not to prove the alternative. The paragraph also clarifies that hypotheses are about population parameters, not sample statistics, and that the null hypothesis typically represents no effect or the status quo.

05:03

📈 Hypothesis Testing with Sales Data

This paragraph presents a practical example of hypothesis testing applied to a sales scenario. Helen, who sells Choco-nutties, is interested in whether offering a free gift increases sales. The paragraph outlines the steps taken to test this hypothesis, including setting up the null and alternative hypotheses, choosing a significance level, collecting sales data, calculating the p-value, and interpreting the results. The example illustrates how a two-tailed test can be used to explore the possibility of increased or decreased sales due to the free gift, and it provides a walkthrough of the statistical analysis process using Excel.

Mindmap

Keywords

💡Hypothesis testing

Hypothesis testing is a statistical method used to make decisions about a population based on sample data. It is central to inferential statistics and involves setting up a null hypothesis (H0) and an alternative hypothesis (H1). The null hypothesis typically represents the status quo or no effect, while the alternative hypothesis represents the effect or difference we are testing for. In the video, hypothesis testing is used to determine if offering a free sticker with choconutties affects sales.

💡Null hypothesis (H0)

The null hypothesis is a statement of no effect or no difference that is tested against an alternative hypothesis. It is a fundamental part of hypothesis testing and is set up to be disproved if evidence to the contrary is found. In the context of the video, the null hypothesis is that there is no difference in the mean sales between days when a free sticker is offered and days when it is not.

💡Alternative hypothesis (H1 or Ha)

The alternative hypothesis is a statement that proposes an effect or difference contrary to the null hypothesis. It is what the researcher is often trying to provide evidence for. In the video, the alternative hypothesis is that there is a difference in mean sales between the two conditions (offering a free sticker vs. not offering one).

💡Significance level (alpha)

The significance level, denoted by alpha, is the probability of rejecting the null hypothesis when it is actually true, also known as a Type I error. It is a threshold that determines when we can say the results of a test are statistically significant. In the video, a significance level of 0.05 is chosen, which is a common convention in statistical testing.

💡Sample

A sample is a subset of a population that is used to represent the entire population in a study. It is crucial in hypothesis testing as it provides the data from which statistics are calculated and inferences about the population are made. In the video, Helen's sales data for 23 days, some with a free sticker and some without, constitute the sample.

💡P-value

The p-value is a statistic that measures the strength of the evidence against the null hypothesis. It is the probability of observing a test statistic as extreme as, or more extreme than, the one calculated from the data assuming the null hypothesis is true. If the p-value is less than the significance level, the null hypothesis is typically rejected. In the video, the p-value obtained from the sales data is used to make a decision about the null hypothesis.

💡Type I error

A Type I error occurs when the null hypothesis is incorrectly rejected when it is actually true. This is also known as a false positive. The significance level determines the maximum probability of making a Type I error. In the context of the video, choosing a significance level of 0.05 means that there is a 5% chance of making a Type I error.

💡Population parameters

Population parameters are numerical values that describe the characteristics of an entire population. In the video, the population parameters of interest are the mean sales figures for all days that choconutties are sold, with and without a free sticker. These are in contrast to sample statistics, which are calculated from the sample data.

💡Two-tailed test

A two-tailed test is a type of hypothesis test that considers differences in both directions from the null hypothesis. It tests for the possibility that the true value could be either less than or greater than the one specified in the null hypothesis. In the video, Helen's test is two-tailed, as she is interested in whether sales increase or decrease with the offer of a free sticker.

💡One-tailed test

A one-tailed test is a type of hypothesis test that considers differences in one direction from the null hypothesis. It is used when the researcher is interested in testing for an effect in a specific direction. If Helen was only interested in whether sales increased with the free sticker and not if they decreased, she would use a one-tailed test.

💡Excel analysis

Excel is a widely used spreadsheet program that can perform various statistical analyses, including hypothesis testing. In the video, Helen uses Excel to calculate the p-value and draw histograms of her sales data, which aids in the analysis of whether offering a free sticker impacts choconutties sales.

Highlights

Hypothesis testing is a key procedure in inferential statistics

Based on the idea that we can tell things about the population from a sample

Hypothesis testing can be explained in five steps: hypotheses, significance, sample, p-value, decide

Decide on your hypotheses: null hypothesis (H0) and alternative hypothesis (H1 or Ha)

Inferential statistics is based on the premise that you cannot prove something to be true, but you can disprove it by finding an exception

The alternative hypothesis is what we're trying to provide evidence for, while the null hypothesis is the opposite or status quo

Hypotheses are always about population parameters, not sample values or statistics

The null hypothesis usually refers to the status quo, representing no effect

The null hypothesis should include a statement of equality, while the alternative should not

Decide on the level of significance (alpha value), typically 0.05

Significance level is the probability of saying the null hypothesis is wrong when it is actually correct (Type 1 error)

Take a sample from the population to provide the statistics needed

Calculate the p-value, usually done by a computer package

Use the p-value to decide whether to reject the null hypothesis. If p-value is less than the significance level, reject the null hypothesis

Example: Helen sells Choco-nutties and wants to test if offering a free gift increases sales

The population is all days of selling Choco-nutties, and the sample is the days in the next month

Null hypothesis: no difference in sales between offering a free sticker and not offering one

Alternative hypothesis: mean sales differ depending on whether a free sticker is offered

Use sample means to make inferences about population means and the difference between them

Two-tailed test is exploratory, interested in differences from zero in both directions

One-tailed test is directional, interested in if sales increase due to the free sticker

Choose a significance level (alpha = 0.05)

Helen collects 23 days of sales data, 13 with free stickers and 10 without

Mean sales are $301.92 with free stickers and $265.83 without

P-value for two-tailed test is 0.02, indicating evidence to reject the null hypothesis

Data suggests a difference in mean sales depending on whether a free sticker is offered

Transcripts

Browse More Related Video

The basic steps of hypothesis testing

P-value in statistics: Understanding the p-value and what it tells us - Statistics Help

P-Value Method For Hypothesis Testing

Using a z-score to complete hypothesis testing for a claim of equality

Elementary Stats Lesson #18

AP Statistics Unit 6 Summary Review Inference for Proportions Part 2 Significance Tests

Hypothesis testing: step-by-step, p-value, t-test for difference of two means - Statistics Help

Takeaways

Q & A

What is the fundamental concept behind hypothesis testing in inferential statistics?

What are the two types of hypotheses typically established in hypothesis testing?

What is the significance level in hypothesis testing, and why is it important?

What is a p-value in the context of hypothesis testing, and how is it used?

How does the example of Helen and her Choco-nutties illustrate the application of hypothesis testing?

What is the difference between a one-tailed and a two-tailed test in hypothesis testing?

Why is it important to use a random process, such as flipping a coin, in Helen's experiment?

What does it mean to reject the null hypothesis in the context of Helen's sales data?

How does the sample mean differ from the population mean in hypothesis testing?

What is the role of Excel or other statistical software in calculating the p-value in hypothesis testing?

What is the implication of the p-value being less than 0.05 in Helen's experiment?