ck12.org normal distribution problems: Empirical rule | Probability and Statistics | Khan Academy
TLDRThis video script provides a detailed explanation of the empirical rule, also known as the 68-95-99.7 rule, applied to a normal distribution problem from ck12.org's AP Statistics book. It uses the example of the mean weight of one-year-old girls in the US, assuming a normal distribution with a mean of 9.5 kg and a standard deviation of 1.1 kg. The script guides viewers through estimating probabilities without a calculator, such as the likelihood of a girl weighing less than 8.4 kg (16%), between 7.3 and 11.7 kg (95%), and more than 12.8 kg (0.15%), highlighting the symmetry and proportions of the normal distribution.
Takeaways
- 📚 The script is discussing a problem from the 'normal distribution' section of an open-source AP Statistics book by ck12.org.
- 🔍 The problem involves estimating the percentage of one-year-old girls in the US that meet a certain weight condition using the empirical rule (68, 95, 99.7 rule).
- 🎯 The mean weight of one-year-old girls is given as 9.5 kilograms with a standard deviation of 1.1 kilograms.
- 🤔 The script emphasizes 'without a calculator estimate', indicating the use of the empirical rule for estimation.
- 📉 The empirical rule states that approximately 68% of data falls within one standard deviation of the mean in a normal distribution.
- 📈 The rule also states that about 95% of data falls within two standard deviations of the mean, and 99.7% within three standard deviations.
- 📊 The script visually demonstrates how to apply the empirical rule to find the probability of weights falling within certain ranges.
- 📌 The probability of a one-year-old girl weighing less than 8.4 kilograms is estimated to be 16% using the empirical rule.
- 🌐 For the weight range between 7.3 and 11.7 kilograms, the probability is 95%, which is within two standard deviations of the mean.
- 🏁 The probability of a one-year-old girl weighing more than 12.8 kilograms is very low, at 0.15%, which is more than three standard deviations above the mean.
- 👶 The script provides a practical example of how to use the empirical rule for estimating probabilities in a normal distribution without a calculator.
Q & A
What is the source of the problem discussed in the script?
-The problem comes from the normal distribution section of CK12.org's AP Statistics book, which is used because it is open source and considered a good resource for practice.
What is the assumed mean weight of one-year-old girls in the US according to the problem?
-The assumed mean weight is 9.5 kilograms, which is a correction from the initially stated 9.5 grams, as the latter would be unrealistic for the weight of a child.
What is the standard deviation of the weight of one-year-old girls mentioned in the script?
-The standard deviation is approximately 1.1 kilograms.
What is the empirical rule, also known as the 68-95-99.7 rule, as discussed in the script?
-The empirical rule states that for a normal distribution, about 68% of values fall within one standard deviation of the mean, 95% fall within two standard deviations, and 99.7% fall within three standard deviations.
How does the script use the empirical rule to estimate the percentage of one-year-old girls weighing less than 8.4 kilograms?
-The script uses the empirical rule to determine that the area representing weights less than one standard deviation below the mean (8.4 kg) is 16%, as the distribution is symmetrical and the total area outside one standard deviation on both sides is 32%.
What is the probability of finding a one-year-old girl weighing between 7.3 and 11.7 kilograms according to the empirical rule?
-According to the empirical rule, there is a 95% chance of finding a one-year-old girl within two standard deviations of the mean, which corresponds to the weight range of 7.3 to 11.7 kilograms.
What is the estimated probability of a one-year-old girl in the US weighing more than 12.8 kilograms?
-The estimated probability is 0.15%, based on the empirical rule that only 0.3% of values fall outside three standard deviations from the mean, and this area is symmetrically distributed on both sides of the mean.
Why is it suggested not to use a calculator for this problem in the script?
-The script suggests not using a calculator because the empirical rule provides a quick estimation method that does not require precise calculation, making it suitable for an estimation without a calculator.
How does the script illustrate the normal distribution and its properties?
-The script uses a freehand drawing to represent the bell curve of the normal distribution, marking the mean and the points one, two, and three standard deviations above and below the mean to demonstrate its symmetrical properties.
What is the significance of the mean and standard deviation in the context of this problem?
-The mean and standard deviation are crucial as they define the normal distribution in the problem. They are used to calculate the range of weights that encompass certain percentages of the population, as per the empirical rule.
How does the script ensure that the reader understands the concept of a normal distribution?
-The script provides a step-by-step explanation of the normal distribution, including a visual representation and a detailed review of the empirical rule, ensuring that the reader grasps the concept before applying it to the problem.
Outlines
📚 Introduction to Normal Distribution Problem
The script introduces a problem from ck12.org's AP Statistics book, which is used due to its open-source nature and quality content. The problem involves estimating the percentage of one-year-old girls in the US with a certain weight, given the mean and standard deviation of their weights. The instructor emphasizes the importance of the empirical rule (68-95-99.7 rule) for normal distributions in solving this problem without a calculator. A brief review of the normal distribution and the empirical rule is provided, explaining the probabilities associated with one, two, and three standard deviations from the mean.
📉 Applying the Empirical Rule to Weight Distribution
This paragraph delves into applying the empirical rule to estimate the probability of one-year-old girls weighing less than 8.4 kilograms. The instructor calculates the weight ranges corresponding to one, two, and three standard deviations from the mean and uses these to determine the areas under the normal distribution curve. The focus is on finding the probability of a weight less than one standard deviation below the mean, which is found to be 16%. The paragraph also covers the probabilities for weights within two standard deviations of the mean (95%) and more than three standard deviations above the mean (0.15%).
🔢 Conclusion on the Probability of Extreme Weights
The final paragraph concludes the problem by focusing on the probability of a one-year-old girl weighing more than 12.8 kilograms, which is three standard deviations above the mean. The instructor uses the empirical rule to determine that this probability is 0.15%. The explanation reinforces the understanding that extreme weights are rare in a normal distribution, and the video script aims to provide a clear and useful explanation of these concepts.
Mindmap
Keywords
💡Normal Distribution
💡Empirical Rule
💡Mean
💡Standard Deviation
💡Symmetric
💡Percentage
💡Calculator
💡Kilograms
💡Probabilities
💡One-Year-Old Girls
💡Estimate
Highlights
Introduction to a problem from the normal distribution section of CK12.org's AP Statistics book.
Use of open-source material for educational purposes.
Assumption of the mean weight of one-year-old girls in the US being normally distributed with a mean of 9.5 kilograms.
Correction of the unit from grams to kilograms for the mean weight.
Explanation of the standard deviation of approximately 1.1 kilograms.
Introduction of the empirical rule, also known as the 68-95-99.7 rule.
Illustration of the normal distribution curve and its properties.
Calculation of weight ranges based on standard deviations from the mean.
Estimation of the percentage of one-year-old girls weighing less than 8.4 kilograms using the empirical rule.
Explanation of the 32% remaining area outside the central 68% in a normal distribution.
Determination of the probability of a one-year-old girl weighing more than one standard deviation above the mean.
Application of the empirical rule to estimate the probability within two standard deviations of the mean.
Calculation of the probability of a one-year-old girl weighing more than 12.8 kilograms.
Use of the empirical rule to find the probability of extreme outcomes more than three standard deviations from the mean.
Final probability estimation of 0.15% for a one-year-old girl weighing more than 12.8 kilograms.
Conclusion summarizing the use of the empirical rule for estimating probabilities in a normal distribution.
Transcripts
Browse More Related Video

k12.org exercise: Standard normal distribution and the empirical | Khan Academy
The Normal Distribution and the 68-95-99.7 Rule (5.2)

Empirical Rule 68-95-99.7 Rule to Find Percentile

Elementary Statistics - Chapter 6 Normal Probability Distributions Part 1
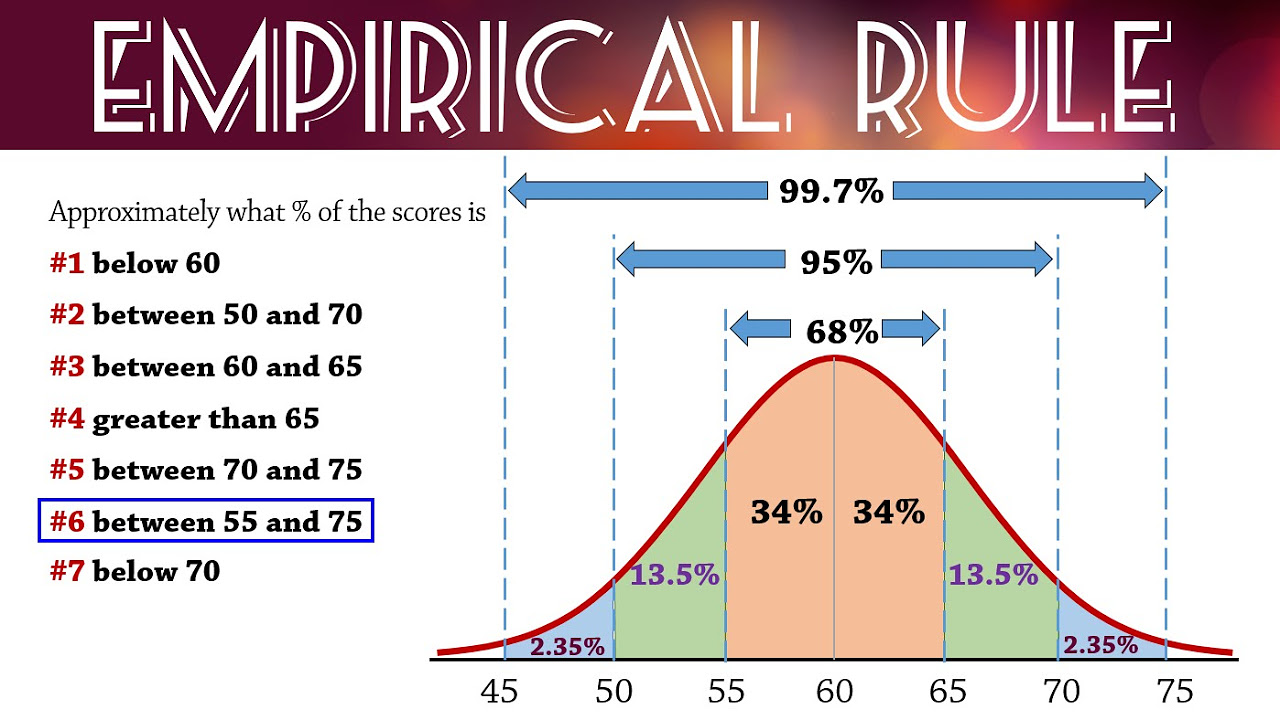
Empirical Rule (68-95-99.7) for Normal Distributions

Normal Distribution & Probability Problems
5.0 / 5 (0 votes)
Thanks for rating: