Normal Distribution & Probability Problems

The Organic Chemistry Tutor

24 Mar 201829:30

EducationalLearning

32 Likes 10 Comments

TLDRThis video script delves into the concept of the normal distribution, illustrating the bell-shaped curve and its significance in statistics. It explains the 68-95-99.7 rule, detailing the probabilities of events occurring within one, two, and three standard deviations from the mean. The script provides a practical application by solving problems related to test scores in a physics class, demonstrating how to calculate percentages and numbers of students within certain score ranges using both the empirical rule and calculus-based integration. The video concludes with a guide on using an online calculator for more precise calculations, emphasizing the importance of understanding the normal distribution in statistical analysis.

Takeaways

📚 The video discusses the normal distribution, also known as the bell-shaped curve, and its significance in statistics.
📉 The population mean (μ) and standard deviation (σ) are central to understanding the normal distribution curve, with μ at the center and σ indicating the spread.
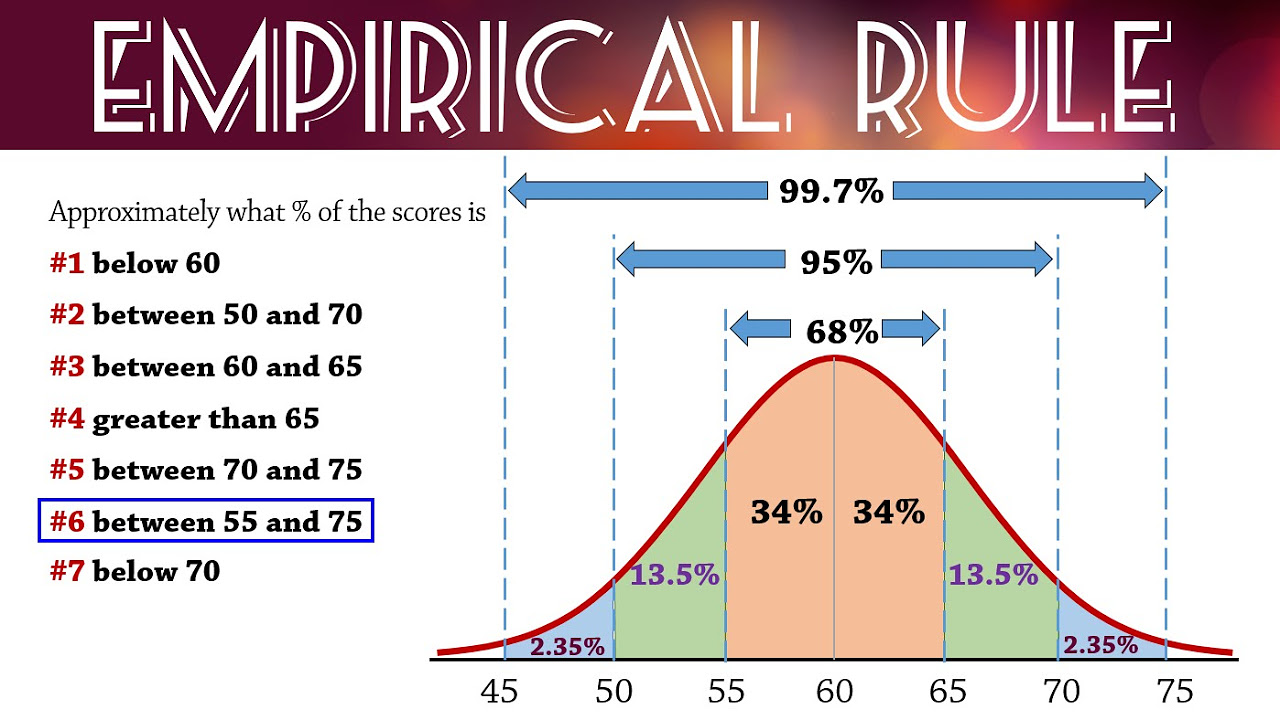
🔢 The 68-95-99.7 rule is crucial for the normal distribution, stating that approximately 68.26% of data falls within one standard deviation of the mean, 95.45% within two, and 99.73% within three.
📊 The area under the curve represents the probability of an event occurring within a certain range, and the video explains how to calculate these probabilities.
📈 The video breaks down the percentages for the regions within one, two, and three standard deviations from the mean, providing exact figures for each segment.
🧩 The symmetry of the normal distribution curve allows for easy calculation of probabilities on either side of the mean by dividing the total percentage by two.
📝 The video emphasizes the importance of noting these percentages for solving problems related to the normal distribution.
🔍 The definite integral of the normal distribution function is introduced as a method for calculating exact probabilities, using calculus and a calculator or an online tool like Wolfram Alpha.
📚 Practice problems are presented to demonstrate the application of the normal distribution in calculating percentages and numbers of students scoring within certain ranges on a test.
🤔 The video provides a step-by-step guide on how to use the normal distribution to solve for the number of students scoring within specific ranges, emphasizing the use of accurate calculations over approximations.
🔧 The use of an online calculator for definite integrals is recommended for obtaining more precise probabilities, with a demonstration of how to input the function into Wolfram Alpha for calculation.

Q & A

What is the normal distribution and why is it significant?
-The normal distribution, also known as the Gaussian distribution or bell-shaped curve, is a continuous probability distribution that is symmetric about the mean, showing the distribution of data points around the average value. It is significant because it is widely used in statistics to model real-valued random variables that cluster around the mean, and it is the basis for many statistical tests and procedures.
What is the population mean (mu) in the context of the normal distribution?
-In the context of the normal distribution, the population mean (mu, μ) is the central value around which all the data points are distributed symmetrically. It represents the average value of the entire population.
What is the standard deviation (Sigma) in the normal distribution?
-The standard deviation (Sigma, σ) is a measure of the amount of variation or dispersion in a set of values in the normal distribution. It indicates how far from the mean (mu) the data points are spread out. One standard deviation away from the mean covers approximately 68.26% of the data points.
What is the 68-95-99.7 rule in relation to the normal distribution?
-The 68-95-99.7 rule, also known as the empirical rule, states that in a normal distribution, approximately 68.26% of the data falls within one standard deviation of the mean, 95.45% falls within two standard deviations, and 99.73% falls within three standard deviations.
How can you calculate the probability of an event occurring between the mean and one standard deviation using the normal distribution?
-The probability of an event occurring between the mean and one standard deviation can be calculated by using the symmetry of the normal distribution curve. It is approximately 34.134% on each side of the mean, totaling 68.268%.
What is the probability of an event occurring between the first and second standard deviations in a normal distribution?
-The probability of an event occurring between the first and second standard deviations is approximately 13.592% on each side of the mean, totaling 27.184%.
How can you estimate the percentage of students scoring between certain ranges in a normally distributed test score dataset?
-You can estimate the percentage by identifying the range on the normal distribution curve that corresponds to the test score range and then applying the empirical rule or using the calculated probabilities for each standard deviation range.
What is the formula for calculating the exact probability between two values (a and b) in a normal distribution using calculus?
-The exact probability between two values (a and b) in a normal distribution is calculated using the definite integral from a to b of the probability density function, which is e^{(-\frac{(x-\mu)^2}{2\sigma^2})} divided by \sigma\sqrt{2\pi}, where μ is the population mean, σ is the standard deviation, and dx represents the differential element.
How can you find the number of students scoring within a specific range in a normally distributed test score dataset with a given total number of students?
-First, calculate the percentage of students scoring within the specific range using the normal distribution probabilities. Then, multiply this percentage by the total number of students to find the approximate number of students within that range.
What is the significance of using an online calculator like Wolfram Alpha for calculating probabilities in the normal distribution?
-An online calculator like Wolfram Alpha can provide more accurate probabilities by evaluating the definite integral of the normal distribution's probability density function between specific limits, especially when dealing with ranges that extend to infinity or require high precision.

Outlines

00:00

📊 Introduction to the Normal Distribution

This paragraph introduces the concept of the normal distribution, also known as the bell curve. It explains the significance of the population mean (mu) and standard deviation (sigma) in the context of the curve. The paragraph also covers the empirical rule, which states that approximately 68.2% of data falls within one standard deviation of the mean, 95.4% within two standard deviations, and 99.7% within three standard deviations. The importance of these percentages is emphasized for solving problems related to the normal distribution.

05:04

📚 Applying the Normal Distribution to Test Scores

The second paragraph delves into applying the normal distribution to a practical example: the test scores of a physics class with 800 students. It demonstrates how to calculate the percentage of students scoring within a certain range of the mean, using both the empirical rule and a more precise calculus-based approach. The paragraph illustrates the process of finding the percentage of students with scores between 68 and 82, highlighting the use of the normal distribution curve and the integral formula for a more accurate calculation.

10:04

🔍 Calculating the Number of Students within a Score Range

This paragraph continues the example from the previous one, focusing on determining the number of students who scored between 61 and 89. It explains how to find the percentage of students within this range by adding the probabilities of the respective regions under the normal distribution curve. The paragraph also shows how to use calculus to confirm this percentage and then convert it into an actual number of students by applying it to the total class size of 800.

15:07

🎯 Estimating Scores Beyond a Certain Threshold

The fourth paragraph discusses the probability of a student scoring within a specific range, such as between 54 and 75, and then extends the discussion to estimating the number of students scoring above a certain threshold, like 96 or more. It explains the process of adding the probabilities of the relevant regions under the curve and using calculus to find a more accurate probability. The paragraph also addresses the challenge of integrating to infinity and suggests using a large number as an approximation for infinity.

20:07

📘 Utilizing Calculus for Normal Distribution Problems

This paragraph provides a detailed explanation of how to use calculus to solve problems related to the normal distribution. It outlines the integral formula for calculating the probability of an event occurring between two points and demonstrates how to plug in the population mean, standard deviation, and the limits of integration into a calculator or an online tool like Wolfram Alpha to find the exact probability.

25:09

🌐 Online Tools for Calculating Normal Distribution

The final paragraph of the script provides guidance on using online calculators, specifically Wolfram Alpha, to calculate probabilities and solve problems related to the normal distribution. It walks through the process of entering the integral expression into the calculator, adjusting the limits of integration for different parts of the problem, and obtaining the probability. The paragraph emphasizes the importance of using accurate and large enough numbers to approximate infinity when necessary.

Mindmap

Keywords

💡Normal Distribution

Normal distribution, also known as Gaussian distribution, is a probability distribution that is characterized by its symmetrical bell-shaped curve. In the context of the video, it represents the distribution of test scores in a physics class, where the mean and standard deviation are key parameters. The video script discusses how to calculate probabilities of different score ranges using this distribution.

💡Bell-Shaped Curve

The bell-shaped curve is a visual representation of the normal distribution, where the highest point of the curve corresponds to the mean of the distribution. The video script uses this term to describe the graphical representation of the test score distribution, emphasizing its symmetry and the areas under the curve that correspond to probabilities.

💡Population Mean (Mu)

The population mean, denoted by the Greek letter mu (μ), is the average value of a population's data set. In the video, the mean is used to center the normal distribution curve, and it is a critical reference point for calculating probabilities of test scores falling within certain ranges.

💡Standard Deviation (Sigma)

Standard deviation, represented by the Greek letter sigma (σ), is a measure of the amount of variation or dispersion in a set of values. The video script explains that one standard deviation away from the mean is a significant point on the normal distribution curve, and it is used to determine the range of scores that encompass a certain percentage of the class.

💡Empirical Rule

The empirical rule, also known as the 68-95-99.7 rule, provides a quick way to estimate the proportion of data that falls within a certain number of standard deviations from the mean in a normal distribution. The video script uses this rule to explain the percentages of test scores within one, two, and three standard deviations from the mean.

💡Probability

Probability is the measure of the likelihood that a particular event will occur, often expressed as a percentage. The video script discusses how the area under the normal distribution curve represents probabilities of events, such as the likelihood of a student scoring within a certain range.

💡Symmetry

In the context of the normal distribution curve, symmetry refers to the mirror-image reflection of the curve around the vertical line passing through the mean. The video script mentions the symmetry of the bell-shaped curve, which implies that the distribution of test scores is equally likely to be above or below the mean.

💡Continuous Random Variable

A continuous random variable is a variable that can take on any value within an interval, as opposed to discrete variables that can only take on certain values. The video script refers to the test scores as a continuous random variable that can vary beyond the mean or below it.

💡Definite Integral

A definite integral is a fundamental concept in calculus that represents the area under a curve between two points on the x-axis. The video script explains how to use definite integrals to calculate the exact probability of a student scoring within a specific range, using the normal distribution curve.

💡Wolfram Alpha

Wolfram Alpha is an online computational knowledge engine that can solve a wide range of problems, including calculus problems. The video script provides an example of how to use Wolfram Alpha to calculate the definite integral for the normal distribution curve, demonstrating an alternative method to manual calculations.

💡Approximation

Approximation in this context refers to the use of estimated values to simplify calculations or to provide a close estimate of a result. The video script mentions approximation when discussing the use of large numbers to represent infinity in definite integrals, as well as rounding percentages to whole numbers for practical purposes.

Highlights

Introduction to the normal distribution and the bell-shaped curve concept.

Explanation of the population mean (mu) and standard deviation (sigma) in the context of the normal distribution.

Visualization of one, two, and three standard deviations from the mean on the normal distribution curve.

The area under the curve represents the probability of an event occurring between two points.

The 68-95-99.7 rule for probabilities within one, two, and three standard deviations from the mean.

Calculation of the percentage of events occurring between the mean and one standard deviation.

Symmetry in the normal distribution curve and its implications for probability calculations.

Method to find the percentage of events between the first and second standard deviations.

Process to determine the percentage of events within three standard deviations of the mean.

Importance of understanding the total probability and area under the curve in a normal distribution.

Application of the normal distribution to solve problems involving test scores and standard deviations.

Use of the definite integral in calculus to find more accurate probabilities in a normal distribution.

How to calculate the percentage of students scoring within a specific range using the normal distribution.

Conversion of probabilities to actual numbers of students based on the total class size.

Approach to find the probability of a student scoring above a certain threshold using the normal distribution.

Demonstration of using an online calculator for definite integrals to solve normal distribution problems.

Final summary of how to apply the normal distribution curve to practical problems in statistics.

Transcripts

Browse More Related Video

Empirical Rule (68-95-99.7) for Normal Distributions

Elementary Statistics - Chapter 6 Normal Probability Distributions Part 1

How to Use the Empirical Rule with Examples

Empirical Rule of Standard Deviation in Statistics

The Normal Distribution and the 68-95-99.7 Rule (5.2)

What is a Bell Curve or Normal Curve Explained?

Related Tags

Normal Distribution Bell Curve Statistical Analysis Standard Deviation Population Mean Probability Theory Calculus Application Wolfram Alpha Physics Test Educational Video Mathematics Tutorial