Points of Inflexion (1 of 2: Understanding & identifying)
TLDRThis video script delves into the intricacies of calculus, focusing on the behavior of functions. It introduces stationary points, where the graph has a horizontal tangent, and distinguishes them from turning points, which are not always stationary. The script further explores points of inflection, which may or may not coincide with stationary points, and emphasizes the importance of recognizing changes in concavity. It provides examples of common and less common types of points of inflection, including those from polynomials and trigonometric functions, and clarifies that while the second derivative being zero often indicates a point of inflection, it is not a definitive rule. The script concludes with a reminder to use a table of values to verify the presence of a point of inflection, highlighting the importance of understanding calculus concepts for a deeper analysis of functions.
Takeaways
- 📚 The script discusses the concept of calculus and its ability to provide deeper insights into the behavior of functions, personifying them with characteristics like increasing, decreasing, and stationary points.
- 🔍 It clarifies the difference between stationary points and turning points, noting that while often related, they are not the same; stationary points do not always indicate a turning point in the function.
- 🔄 The script introduces the concept of points of inflection, which are related to but distinct from stationary points, characterized by a change in concavity without necessarily being a stationary point.
- 📈 Points of inflection can occur in various forms, including those that are not stationary, and are often found in polynomial functions, which are common in calculus.
- 📚 The importance of understanding the second derivative, \( d^2y/dx^2 \), is highlighted as it helps in identifying points of inflection where there is a change in concavity.
- 🤔 The script warns against the common mistake of assuming that finding where the second derivative equals zero is sufficient to identify all points of inflection, as this is not always the case.
- 👀 It provides a method to visualize points of inflection by covering parts of the graph to observe changes in concavity, though this is not a formal proof but rather a conceptual aid.
- 📉 The transcript includes an example of the cube root of \( x \) to illustrate a point of inflection where the second derivative does not exist, emphasizing the need to look beyond the second derivative for inflection points.
- 📊 The use of a Venn diagram is suggested to understand the relationship between points of inflection and the second derivative, showing overlap where both conditions are met.
- 📝 The importance of testing the vicinity of a suspected point of inflection is stressed, as the function's behavior can vary and may require testing closer to the suspected point.
- 🚫 The script cautions against prematurely concluding that a point of inflection has been found just because the second derivative equals zero, emphasizing the need for further analysis.
Q & A
What is the primary focus of the discussion in the transcript?
-The primary focus of the discussion is on understanding calculus concepts related to functions, specifically stationary points, turning points, and points of inflection.
How are stationary points and turning points different?
-Stationary points are where the graph of a function has a horizontal tangent, while turning points are where the function changes direction, from increasing to decreasing or vice versa. Not all stationary points are turning points, and not all turning points are stationary points.
What is a point of inflection?
-A point of inflection is a point on the graph of a function where the concavity changes. It is where the function transitions from being concave up to concave down or vice versa.
How is a point of inflection related to the second derivative of a function?
-A point of inflection is often associated with the second derivative being equal to zero. However, it's important to note that a point of inflection can exist even if the second derivative does not exist at that point.
Why is it incorrect to assume that finding where the second derivative is zero is sufficient to identify all points of inflection?
-While many points of inflection coincide with the second derivative being zero, there are exceptions where the second derivative does not exist or is not zero, yet the function still exhibits a change in concavity, such as with the cube root of x.
What is the significance of the example involving x to the power of 4?
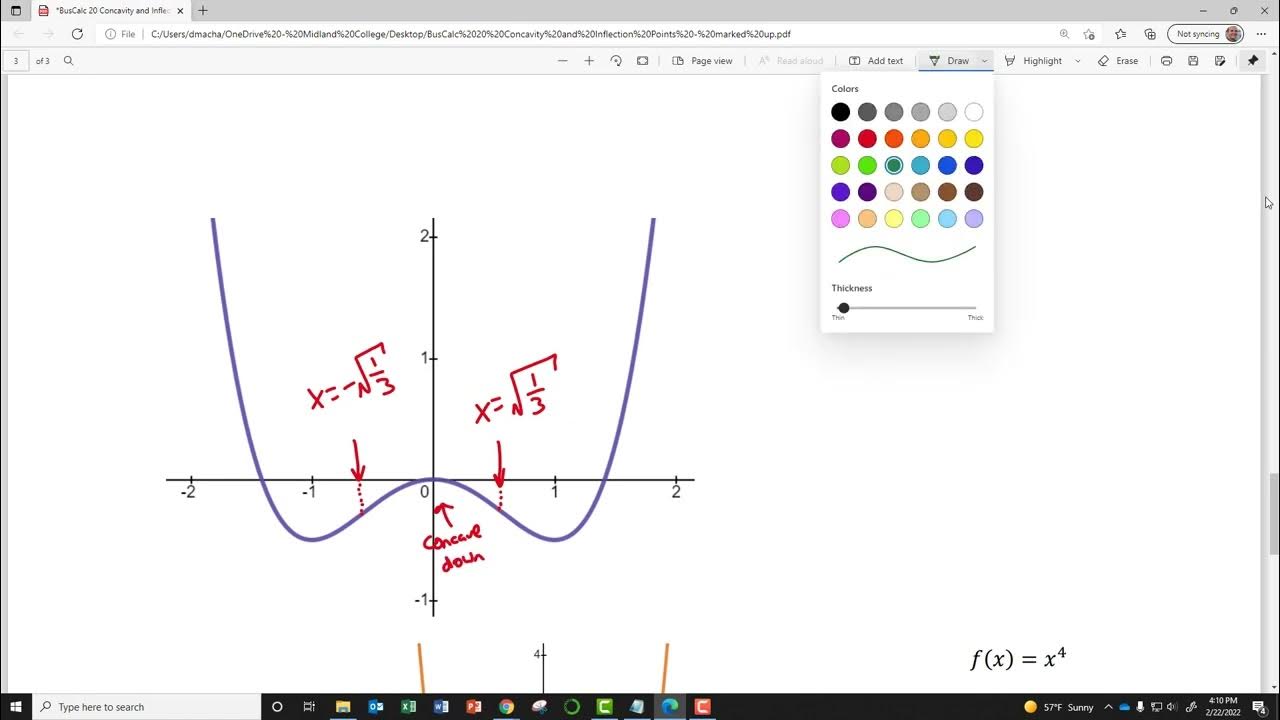
-The example of x to the power of 4 is used to illustrate that even when the second derivative is zero, it does not necessarily indicate a point of inflection. The function is concave up on both sides of the point where the second derivative is zero, indicating no change in concavity.
What is the recommended approach to identify points of inflection?
-After finding where the second derivative is zero or does not exist, one should calculate a table of values to test the concavity on either side of the suspected point of inflection to confirm a change in concavity.
What is the importance of understanding the difference between stationary points and points of inflection?
-Understanding the difference is crucial for accurately analyzing the behavior of functions. Each concept provides unique insights into how a function behaves, and混淆 (confusion) between them can lead to incorrect conclusions about the function's properties.
How does the concept of 'concavity' help in visualizing points of inflection?
-The concept of concavity helps in visualizing points of inflection by observing the curvature of the function. If the curvature changes from concave up to concave down or vice versa, it indicates a point of inflection.
Why are polynomials often used as examples when discussing points of inflection?
-Polynomials are common examples in discussions of points of inflection because they are simple, well-understood functions that frequently exhibit the behavior of changing concavity, making them ideal for illustrating the concept.
What is the role of the first derivative in identifying stationary points but not in identifying points of inflection?
-The first derivative is used to find stationary points by identifying where the derivative is zero or undefined (indicating a vertical tangent). However, for points of inflection, it is the second derivative that is of interest, as it relates to the concavity of the function.
Outlines
📈 Understanding Calculus and Function Behavior
This paragraph discusses the depth of knowledge one gains about functions through calculus. It personifies functions, describing their behaviors like characters with actions such as increasing, decreasing, and having stationary points. The focus is on stationary points and turning points, explaining their relationship and the common confusion between them. The concept of points of inflection is introduced, which are related to stationary points but not necessarily the same. The speaker also touches on the existence of points where functions turn without a stationary point, which is less common but significant for understanding the complexity of function behavior.
🔍 Identifying Points of Inflection and Second Derivatives
The second paragraph delves into the intricacies of points of inflection, which are sometimes confused with stationary points. It emphasizes the need for a second diagram to better illustrate the concept. Points of inflection are characterized by a change in concavity, which can be observed in polynomial functions. The speaker provides examples of common and less common types of points of inflection, including the cube root of x, which has a unique behavior due to the lack of a second derivative at certain points. The importance of recognizing that not all points of inflection will have a second derivative equal to zero is highlighted, and the potential for error in assuming that finding the second derivative is sufficient to identify all points of inflection is cautioned against.
📊 Using a Table of Values to Find Points of Inflection
The final paragraph explains the process of using a table of values to identify points of inflection. It clarifies that this method differs from determining the nature of stationary points and focuses on the second derivative instead. The speaker advises on the importance of testing the function's behavior in the vicinity of a suspected point of inflection to confirm a change in concavity. The process involves establishing whether the function transitions from concave up to concave down or vice versa, which is key to identifying a true point of inflection. The paragraph concludes with a reminder to not confuse this table with methods used for stationary points and to be mindful of the function's specific characteristics when determining the vicinity for testing.
Mindmap
Keywords
💡Calculus
💡Function
💡Stationary Points
💡Turning Points
💡Points of Inflection
💡Concavity
💡Second Derivative
💡Polynomials
💡Trigonometric Functions
💡Vertical Tangent
💡Table of Values
Highlights
Calculus allows for a deeper understanding of functions, including their behavior, increases, decreases, and stationary points.
Stationary points are where the graph stops or has a horizontal tangent.
Turning points are closely related to stationary points but are not always the same; some stationary points do not turn.
There are instances where functions turn without a stationary point, indicating a lack of horizontal tangent.
Points of inflection are related to stationary points and can be identified by a change in concavity and a horizontal tangent.
Not all points of inflection are stationary points; some show a change in concavity without a horizontal tangent.
Common types of points of inflection are encountered in polynomials, such as cubics and quartics.
Trigonometric functions, once their calculus is understood, often exhibit points of inflection without a full turn.
The concept of covering part of a graph to visualize changes in concavity is a useful technique for identifying points of inflection.
The cube root of x is an example of a function with a change in concavity but without a stationary point or a second derivative at the point of change.
Even powers of x, such as x^4, x^6, etc., have a second derivative equal to zero but are not points of inflection as they do not show a change in concavity.
When finding points of inflection, it is crucial to not stop at finding the second derivative equal to zero but to further analyze the change in concavity.
A table of values focusing on the second derivative, rather than the first, is used to determine points of inflection.
The vicinity for testing the second derivative depends on the specific function and may require testing closer intervals.
Identifying a point where the second derivative is zero does not confirm a point of inflection; a change in concavity must also be established.
The process of finding points of inflection involves understanding the function's behavior and using calculus to analyze changes in concavity.
It is an error to assume that finding the second derivative equal to zero is sufficient to identify all points of inflection.
Points of inflection may exist without the second derivative being zero, requiring a deeper analysis of the function's curvature.
Transcripts
Browse More Related Video

Using the Second Derivative (2 of 5: Turning Point vs Stationary Point analogy)

Critical points & Stationary points

Using the Second Derivative (3 of 5: Why the Points of Inflexion may not exist when f"(x) = 0)

Using the Second Derivative (2 of 2: Determining nature of stationary points)
BusCalc 20 Concavity and Inflection Points

Inflection Point Grade 12
5.0 / 5 (0 votes)
Thanks for rating: