Critical points & Stationary points

Transcended Institute
29 Oct 202318:16
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script delves into the concept of stationary and critical points in calculus. It explains that stationary points, where the derivative dy/dx equals zero, represent a function's constant rate of change, indicating neither an increase nor decrease. The script clarifies the difference between stationary points, which include maxima, minima, and points of inflection, and critical points, which are a broader set that also includes points where the derivative does not exist. The speaker illustrates these concepts with graphs and provides examples, including how to find critical points by setting the derivative equal to zero for functions like x^3 - 3x^2 - 9x + 5, an exponential function, and others. The goal is to solidify understanding through practice problems, emphasizing the importance of differentiating functions and analyzing the second derivative to determine the nature of stationary points.

Takeaways
  • 📚 The term 'stationary points' refers to points on a graph where the derivative (dy/dx) is equal to zero, indicating no change in the function's rate of increase or decrease.
  • 📈 Stationary points can be further classified into maxima, minima, and points of inflection, which are determined by analyzing the first and second derivatives of a function.
  • 🔍 A point of inflection is where the second derivative is zero, indicating a change in the concavity of the function without being a maximum or minimum.
  • 📉 Maxima and minima are determined by the second derivative test: a positive second derivative indicates a minimum, while a negative second derivative indicates a maximum.
  • 🤔 The concept of 'stationary' comes from the fact that at these points, the function neither increases nor decreases, hence it is 'stationary' or constant.
  • 📌 Critical points are a broader set that includes stationary points and points where the derivative does not exist, such as points where the function is undefined.
  • 🔢 To find critical points, one must differentiate the function and set the derivative equal to zero, solving for the variable to find the x-values.
  • 📐 For functions where the derivative is undefined at certain points (like division by zero), these points are also considered critical points.
  • 📝 The practice questions provided in the script illustrate the process of finding critical points by differentiating and solving for when the derivative equals zero or does not exist.
  • 🧐 Understanding the difference between stationary and critical points is crucial, as critical points encompass a wider range of scenarios, including undefined derivatives.
  • 📚 The script uses examples of exponential functions and natural logs to illustrate the concept of increasing at an increasing or decreasing rate, which is key to understanding the behavior of functions at stationary points.
Q & A

  • What are stationary points in calculus?

    -Stationary points, also known as critical points, are points on the graph of a function where the derivative (dy/dx) is equal to zero. At these points, the function is neither increasing nor decreasing, hence the term 'stationary'.

  • Why are stationary points called 'stationary'?

    -The term 'stationary' comes from the fact that at these points, the function's rate of change is zero. It signifies no change in the function's value, hence it is 'stationary'.

  • What is the relationship between stationary points and the derivative of a function?

    -Stationary points are directly related to the derivative of a function. They occur where the derivative (dy/dx) equals zero, indicating a potential maximum, minimum, or point of inflection on the graph of the function.

  • How do you find stationary points on a graph?

    -To find stationary points on a graph, you would typically calculate the derivative of the function and set it equal to zero. The solutions to this equation will give you the x-values of the stationary points, which you can then use to find the corresponding y-values.

  • What are the different types of stationary points?

    -There are three types of stationary points: maxima, minima, and points of inflection. Maxima and minima represent the highest and lowest points on the graph, respectively, while points of inflection indicate a change in the concavity of the graph.

  • What is the difference between a critical point and a stationary point?

    -A critical point is a broader concept that includes stationary points. Critical points occur where the derivative of a function is zero or where the derivative does not exist. Stationary points are a subset of critical points where the derivative is specifically zero.

  • How can you determine if a stationary point is a maximum, minimum, or point of inflection?

    -The second derivative test can help determine the nature of a stationary point. If the second derivative is positive at a stationary point, it indicates a local minimum. If it is negative, it indicates a local maximum. If the second derivative is zero, the test is inconclusive, and further analysis is required.

  • What is the significance of the second derivative in analyzing stationary points?

    -The second derivative provides information about the concavity of the function. A positive second derivative indicates that the function is concave up (shaped like a U), suggesting a minimum, while a negative second derivative indicates that the function is concave down (inverted U shape), suggesting a maximum.

  • Can you provide an example of how to find critical points of a function?

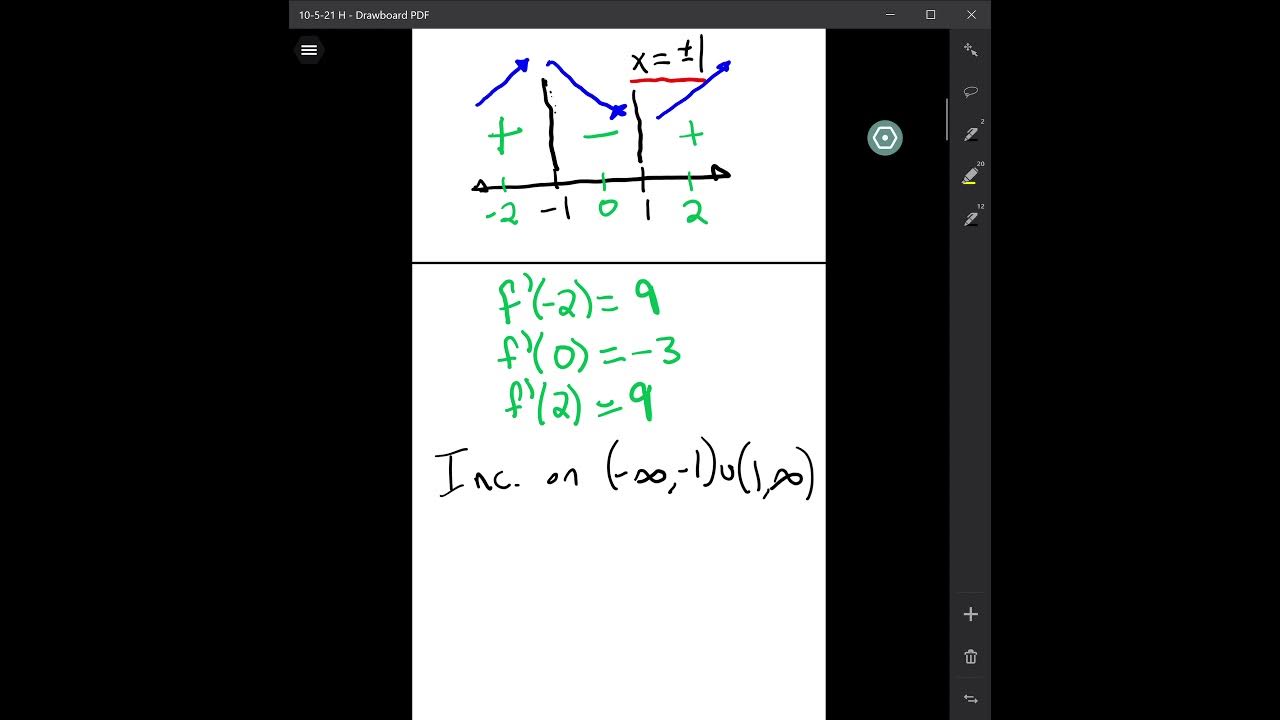
    -Certainly. Consider the function f(x) = x^3 - 3x^2 - 9x + 5. To find the critical points, first differentiate the function to get f'(x) = 3x^2 - 6x - 9. Then set the derivative equal to zero: 3x^2 - 6x - 9 = 0. Solving this quadratic equation will give the x-values of the critical points. Substitute these x-values back into the original function to find the corresponding y-values.

  • What happens when the derivative of a function is undefined at a certain point?

    -When the derivative of a function is undefined at a certain point, that point is still considered a critical point. This often occurs at points where the function has a vertical tangent or a sharp corner, such as at x = 0 for the function 1/x.

  • Can you give an example of a function where the derivative is undefined at a certain point?

    -An example of such a function is f(x) = 1/x. The derivative of this function, f'(x), is undefined at x = 0 because the function approaches infinity as x approaches zero, making the derivative undefined at that point.

Outlines
00:00
📚 Introduction to Stationary Points

The video begins with an exploration of stationary points in calculus. The instructor explains that stationary points are where the derivative of a function, dy/dx, equals zero. This is typically where the function's rate of change is at a standstill, neither increasing nor decreasing. The concept is illustrated with a graph that shows various parts of a function increasing and decreasing, with the stationary points being where the tangent to the curve is parallel to the x-axis. The instructor also discusses the origin of the term 'stationary' and provides examples of functions, such as exponential functions and natural logarithms, to illustrate increasing and decreasing rates.

05:01
🔍 Understanding Points of Inflection and Critical Points

The second paragraph delves deeper into the concept of stationary points by introducing points of inflection and critical points. Points of inflection are identified as locations where the first derivative is zero, but the function is neither at a maximum nor minimum. The instructor clarifies that critical points encompass stationary points and also include points where the derivative of the function does not exist. The importance of the second derivative in determining whether a stationary point is a maximum, minimum, or point of inflection is highlighted. The video then presents a practice question involving the function f(x) = x^3 - 3x^2 - 9x + 5, guiding viewers through the process of finding its critical points by setting the derivative equal to zero.

10:02
📈 Advanced Examples of Finding Critical Points

In this segment, the instructor tackles more complex functions to demonstrate finding critical points. The first example involves an exponential function, where the derivative involves the natural logarithm of the base. The instructor shows how to set the derivative equal to zero and solve for the variable to find the critical point. The second example features a function with a variable to the power of two-thirds, and the instructor explains how to simplify the derivative and find the critical point by setting it to zero. The importance of understanding the derivative's behavior when it is undefined, as this also constitutes a critical point, is emphasized.

15:05
📘 Practice Questions for Critical Point Determination

The final paragraph provides two practice questions for the viewers to apply their understanding of critical points. The first question involves a function with an exponential term, and the second involves a rational function. The instructor encourages viewers to pause the video and attempt to determine the critical points for these functions on their own. This serves as a practical exercise to reinforce the concepts discussed throughout the video and to test the viewers' ability to identify critical points in various mathematical contexts.

Mindmap
Keywords
💡Stationary Points
Stationary points, also known as critical points, are locations on a graph where the derivative of a function, dy/dx, equals zero. They represent points of equilibrium, where the function neither increases nor decreases. In the video, stationary points are discussed as the points where the tangent to the curve is parallel to the x-axis, indicating no change in the rate of the function's increase or decrease. Examples given include points of maxima, minima, and points of inflection.
💡Critical Points
Critical points encompass a broader set than stationary points and include not only points where the derivative is zero but also where the derivative does not exist. They are pivotal in calculus for identifying potential maxima, minima, and points of inflection. The script explains that critical points are where dy/dx equals zero or where the function itself is not defined, such as at points where the denominator of a fraction becomes zero.
💡Derivative
The derivative of a function, often represented as dy/dx or f'(x), measures the rate at which the function's value changes with respect to changes in its variable. In the context of the video, finding the derivative is the first step in identifying critical and stationary points. It is used to determine where the rate of change is zero, which corresponds to stationary points.
💡Maxima
A maxima is a point on a graph where the function reaches its highest value within a certain domain. The video explains that to identify a maxima, one would look for a point where the second derivative is less than zero, indicating that the function is concave down and has reached a peak.
💡Minima
Minima are points on a graph where the function attains its lowest value within a certain domain. The script mentions that a minima is identified when the second derivative is greater than zero, which means the function is concave up and has reached a trough.
💡Points of Inflection
A point of inflection is a point on the graph of a function where the curve changes its concavity up or down. The video describes it as a point where the function's rate of change is zero (dy/dx = 0), but it is neither a maxima nor a minima. It is a change in the function's behavior rather than an extreme value.
💡Second Derivative
The second derivative of a function, denoted as d²y/dx² or f''(x), provides information about the concavity of the function. It is used to determine whether a stationary point is a maxima, minima, or point of inflection. The video script explains that a positive second derivative indicates a concave up function (minimum), while a negative second derivative indicates a concave down function (maximum), and a zero second derivative suggests a point of inflection.
💡Exponential Function
An exponential function is a mathematical function where the variable is in the exponent. The video script uses the exponential function as an example to illustrate how a function can increase at an increasing rate. It is differentiated to find its derivative, which is crucial for identifying critical points.
💡Natural Logarithm
The natural logarithm, often denoted as ln(x), is the logarithm of a number with the base e (Euler's number, approximately equal to 2.71828). In the video, the natural logarithm function is used as an example of a function that increases at a decreasing rate, contrasting with the exponential function.
💡Practice Questions
Practice questions are used in the video to solidify the concepts discussed, such as finding critical points of given functions. The script provides examples of functions, like f(x) = x^3 - 3x^2 - 9x + 5, and guides the viewer through the process of differentiating the function, setting the derivative equal to zero, and solving for x to find the critical points.
Highlights

Introduction to stationary and critical points in calculus.

Stationary points are where the derivative (dy/dx) equals zero.

The term 'stationary' refers to points where the function neither increases nor decreases.

Critical points include stationary points and points where the derivative does not exist.

Differentiation of functions is key to finding critical points.

Example given: finding critical points of a cubic function f(x) = x^3 - 3x^2 - 9x + 5.

Methodology for solving: set the derivative equal to zero and solve for x.

Using the second derivative to determine if a point is a maximum, minimum, or point of inflection.

Explanation of how to find the y-values for critical points by substituting x-values back into the original function.

Differentiating an exponential function and finding its critical points.

Using natural logarithms to solve for variables in exponential functions.

Handling functions with undefined derivatives as critical points.

Practice questions to solidify understanding of finding critical points.

Advanced example involving a function with a power of 2/3.

Clarification that a function's undefined point at x=0 is a critical point.

Encouragement for viewers to try practice questions involving different types of functions.

Transcripts

Browse More Related Video

Relative Maxima/Minima Examples

Inflection Point Grade 12

Differentiation (Maxima and Minima)

Using the Second Derivative (1 of 5: Finding the Point of Inflexion)

Finding Stationary Points and Determining their Nature

BusCalc 14.3 Extrema of Multivariable Functions

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusStationary PointsCritical PointsDerivativesGraph AnalysisMaxima MinimaInflexion PointsMathematics EducationProblem SolvingEducational Content