Using the Second Derivative (2 of 5: Turning Point vs Stationary Point analogy)

Eddie Woo
13 Dec 201509:11
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script focuses on the distinction between stationary points and turning points in calculus, emphasizing the importance of understanding points of inflection. It clarifies that while all turning points are stationary, not all stationary points are turning points. The script defines a turning point as where the gradient changes sign, and a point of inflection as where the concavity changes sign. It also discusses the limitations of using tables of values and the second derivative in finding points of inflection, advocating for a visual approach to identify changes in concavity by observing the graph. The transcript provides practical advice on how to identify these points by visual inspection rather than relying solely on mathematical formulas.

Takeaways
  • 📌 The distinction between stationary points and turning points is crucial, with turning points always being stationary but not vice versa.
  • 🔍 Points of inflection are different from turning points and should not be confused with stationary points.
  • 📈 A turning point is characterized by a change in the sign of the gradient, either from negative to positive or vice versa.
  • 📊 To identify turning points, one can look for where the graph's gradient changes sign, indicating a change from increasing to decreasing or decreasing to increasing.
  • 🚫 Not all stationary points are turning points; a stationary point requires the derivative to be zero, but a turning point may occur without a derivative at that point.
  • 💡 The concept of a point of inflection is introduced as a change in the sign of concavity, rather than the gradient.
  • 📐 Finding points of inflection involves looking for changes in concavity, which may not necessarily be indicated by the second derivative being zero.
  • 👀 Visual inspection of a graph can be a powerful tool for identifying points of inflection, such as by covering parts of the graph to observe changes in concavity.
  • 📉 A point of inflection can be approximated by looking for changes in the graph's shape, such as from concave up to concave down or vice versa.
  • 💧 A simple analogy to understand points of inflection is to imagine water poured on the graph; water would rest in concave areas, indicating points where the concavity changes.
  • 📚 The script emphasizes the importance of understanding the conceptual differences between stationary points, turning points, and points of inflection for accurate analysis of mathematical functions.
Q & A

  • What is the main difference between stationary points and turning points?

    -Stationary points occur where the derivative (gradient) is zero, while turning points are where the gradient changes sign from negative to positive or vice versa. Not all stationary points are turning points, but all turning points are stationary points.

  • Why are turning points important in the context of this script?

    -Turning points are important because they mark a change in the sign of the gradient, indicating a change in the direction of the function from increasing to decreasing or vice versa.

  • What is a point of inflection and how does it differ from a turning point?

    -A point of inflection is a point where the concavity of a function changes. Unlike turning points, which involve a change in the sign of the gradient, points of inflection do not necessarily involve a change in the gradient's value or sign.

  • How can you identify a turning point on a graph without calculus?

    -A turning point can be identified by looking for a change in the sign of the gradient on the graph. If the graph goes from increasing to decreasing or decreasing to increasing, there is likely a turning point.

  • What is the significance of the second derivative in finding points of inflection?

    -The second derivative can help identify points of inflection because it measures the concavity of the function. If the second derivative changes sign, it indicates a change in concavity, which is a point of inflection.

  • How does the script suggest finding points of inflection on a graph?

    -The script suggests using a visual approach by covering parts of the graph to identify changes in concavity. When the concavity changes from concave up to concave down or vice versa, that indicates a point of inflection.

  • Why is it incorrect to assume that a point where the second derivative is zero is always a point of inflection?

    -A point where the second derivative is zero is not always a point of inflection because there could be other factors, such as discontinuities, that affect the concavity of the function.

  • What is the relationship between the concavity of a function and its second derivative?

    -The concavity of a function is related to the sign of its second derivative. If the second derivative is positive, the function is concave up; if it's negative, the function is concave down.

  • Can a function have a turning point without being differentiable at that point?

    -Yes, a function can have a turning point without being differentiable at that point. The script provides an example of a function that has a turning point at the origin, but the derivative does not exist there.

  • What is the practical method suggested in the script to determine the concavity of a function?

    -The script suggests a practical method of determining concavity by imagining pouring water over the graph. The areas where water would rest indicate concave up regions, while areas where water would roll off indicate concave down regions.

  • Why is it necessary to look at the values before and after a point when determining a change in concavity?

    -It is necessary to look at the values before and after a point to determine a change in concavity because a point of inflection requires a change in the sign of the concavity. Checking the values before and after helps confirm this change.

Outlines
00:00
📚 Understanding Stationary and Turning Points

This paragraph discusses the distinction between stationary points and turning points in calculus. It emphasizes that while all turning points are stationary, not all stationary points are turning points. The focus is on points of reflection, which are likened to turning points but differ in that they mark a change in concavity rather than the gradient. The explanation clarifies that a turning point is where the gradient changes sign from negative to positive or vice versa. The paragraph also highlights the importance of not confusing stationary points with turning points, especially when the function is not differentiable at a turning point, as illustrated with an example function.

05:00
🔍 Identifying Points of Inflection with Graph Analysis

The second paragraph delves into the concept of points of inflection, advising viewers to think of them in terms of changes in concavity rather than stationary points. It explains that points of inflection are where the concavity changes sign, and this is crucial for finding them without relying solely on calculus methods. The paragraph suggests a practical, visual technique for identifying points of inflection by covering parts of a graph to observe changes in concavity. It also discusses the limitations of using tables of values and the importance of examining the graph before and after a suspected point of inflection to confirm a change in concavity. The summary concludes with a simplified approach to understanding concavity changes by imagining water resting on the graph, highlighting areas where water would collect or roll off, indicating changes in concavity.

Mindmap
Keywords
💡Stationary Points
Stationary points are points on a graph where the derivative of a function is zero or undefined, indicating no change in the slope of the function at that point. In the video, stationary points are discussed as a preliminary step to identifying turning points, but it's clarified that not all stationary points are turning points. The script uses the example of a graph to illustrate that some turning points are not stationary because they lack differentiability, such as at a sharp corner or cusp.
💡Turning Points
Turning points are a specific type of stationary point where the function changes direction, either from increasing to decreasing or vice versa. This is identified by the gradient (first derivative) changing from positive to negative or negative to positive. The video emphasizes that while all turning points are stationary, not all stationary points are turning points, which is a subtle but important distinction for understanding changes in the function's behavior.
💡Points of Inflection
Points of inflection are locations on a graph where the function changes concavity, but not necessarily its monotonicity (whether it is increasing or decreasing). The video script explains that a point of inflection marks a change in the sign of the concavity, which can be detected by observing changes in the graph's shape from concave up to concave down or vice versa. This concept is crucial for understanding the overall curvature and shape of a function's graph.
💡Gradient
The gradient, also known as the derivative, is a measure of the slope or steepness of a function at a particular point. In the context of the video, the gradient is used to identify turning points, where it changes sign. The script mentions that a turning point occurs where the gradient goes from negative to positive or from positive to negative, indicating a change in direction of the function.
💡Concavity
Concavity refers to the curvature of a function. A function is said to be concave up if its graph curves upward like a U shape, and concave down if it curves downward like an inverted U shape. The video uses the concept of concavity to explain points of inflection, which occur when there is a change in the sign of the concavity, indicating a change in the function's curvature.
💡Second Derivative
The second derivative of a function is the derivative of the first derivative and provides information about the function's concavity. In the video, it is mentioned that finding where the second derivative is zero can help identify points of inflection. However, the script also cautions that the second derivative being zero is not the only way to find a point of inflection, as there can be changes in concavity due to discontinuities.
💡Differentiability
Differentiability is a property of a function that means it has a derivative at a given point. The video script points out that for a point to be a stationary point, it must be differentiable, which is not the case at points like sharp corners or cusps where the derivative does not exist.
💡Discontinuities
Discontinuities are points on a graph where a function is not defined or its derivative does not exist. The video script uses discontinuities as an example to illustrate that a turning point can occur at a point where the function is not differentiable, such as at a sharp turn or cusp in the graph.
💡Sign Change
A sign change refers to when a mathematical quantity changes from positive to negative or from negative to positive. In the video, sign change is used to describe both turning points, where the gradient changes sign, and points of inflection, where the concavity changes sign. The script emphasizes that identifying these sign changes is key to understanding the behavior of a function at specific points.
💡Graph Interpretation
Graph interpretation involves analyzing the visual representation of a function to understand its properties. The video script discusses various techniques for interpreting graphs, such as looking for changes in concavity or gradient to identify points of inflection and turning points. It also suggests practical methods like covering parts of the graph to more easily spot changes in concavity.
Highlights

Differentiation between stationary points and turning points is crucial in understanding points of reflection.

Turning points are always stationary points, but not all stationary points are turning points.

A turning point is defined as where the gradient changes sign from negative to positive or vice versa.

Turning points can be identified by a change in the sign of the gradient to the left and right of the point.

Not all graphs with turning points have stationary points, as demonstrated by a piecemeal function example.

The origin is a turning point but not a stationary point due to non-differentiability.

Points of inflection are similar to turning points but relate to changes in concavity rather than gradient.

A point of inflection marks a change in the sign of concavity.

Finding points of inflection involves looking for changes in concavity rather than just second derivative zeros.

Discontinuities can change concavity without a change in the second derivative.

Using a secondary function helps in identifying points of inflection without relying on a table of values.

A practical method to find points of inflection is by visually covering parts of the graph to detect concavity changes.

The graph's visual inspection can reveal points of inflection more dramatically than numerical methods.

Points of inflection can be approximated on a graph without exact function values.

Understanding the function's behavior around points of inflection is essential, even without exact values.

Graphical representation can sometimes be more intuitive for identifying points of inflection than algebraic methods.

A simple analogy of water resting on the graph helps visualize points of inflection as areas where water would collect.

Differentiating between changes in gradient and concavity is key to correctly identifying points of inflection.

Transcripts

Browse More Related Video

Points of Inflexion (1 of 2: Understanding & identifying)

Inflection Point Grade 12

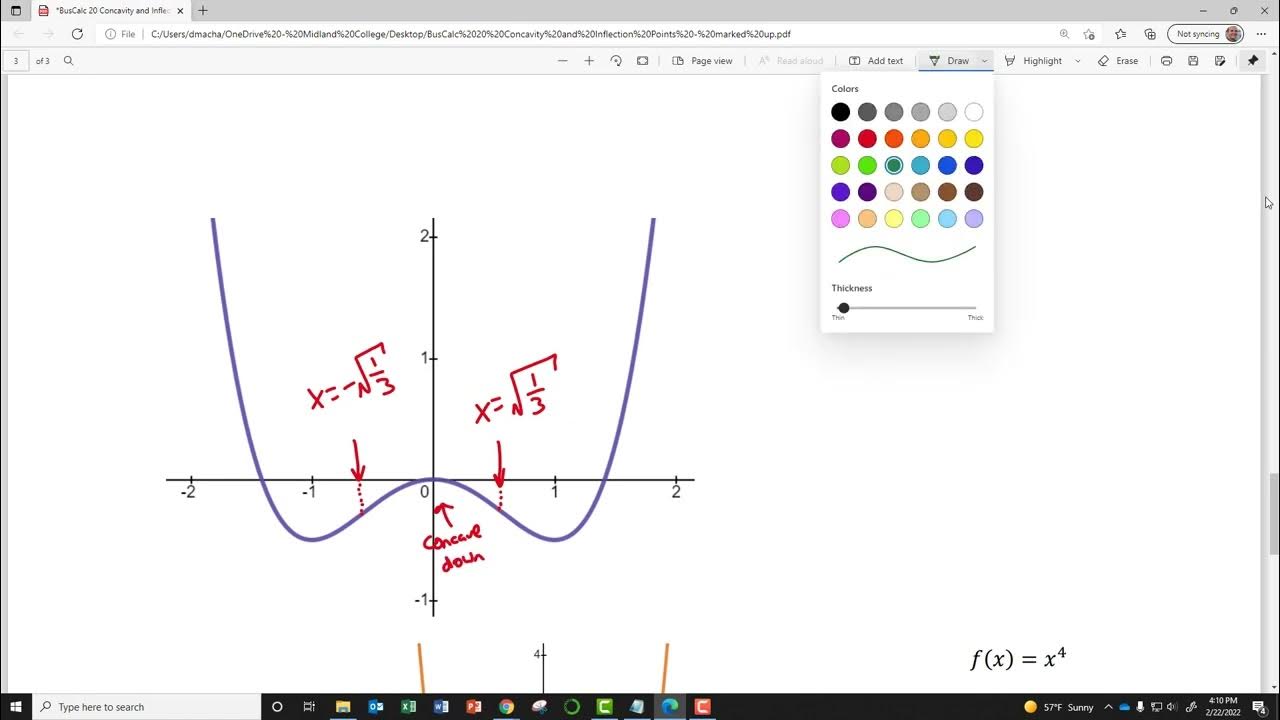
BusCalc 20 Concavity and Inflection Points

Using the Second Derivative (3 of 5: Why the Points of Inflexion may not exist when f"(x) = 0)

Concavity, Inflection Points, and Second Derivative

Inflection points (graphical) | AP Calculus AB | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusStationary PointsTurning PointsPoints of InflectionGradient ChangesConcavityMath EducationGraphical AnalysisDerivative ConceptEducational Content