BusCalc 20 Concavity and Inflection Points

Drew Macha
22 Feb 202215:45
EducationalLearning
32 Likes 10 Comments

TLDRIn this informative video, the concept of concavity and inflection points is explored in the context of both physics and mathematics. The presenter begins by contrasting convex and concave lenses, using visual aids to illustrate the differences. The discussion then shifts to the mathematical interpretation, where concavity is determined by the sign of a function's second derivative: positive for concave up and negative for concave down. The video provides clear examples to demonstrate how to identify intervals of concavity and locate inflection points, which are where the concavity changes. The presenter emphasizes that not every zero second derivative indicates an inflection point, but an inflection point always results in a zero second derivative. The video concludes with several examples, illustrating how to calculate derivatives, identify potential inflection points, and verify their existence by evaluating the concavity on either side of the suspected point. This comprehensive overview is designed to enhance understanding of these mathematical principles, making them accessible to viewers.

Takeaways
  • 🔍 **Concavity and Convexity in Optics**: Lenses can be either concave (curved inwards) or convex (curved outwards), which is important in the study of optics.
  • 📈 **Mathematical Concavity**: In mathematics, concavity refers to whether a curve or function is concave up (like a 'U') or concave down (inverted 'U') over certain intervals.
  • 🌧️ **Visualizing Concavity**: A simple way to remember concave up is by imagining a curve that could hold rainwater, whereas concave down curves would let the water spill out.
  • 📌 **Intervals of Concavity**: For a given function, it's important to identify intervals where it is concave up or concave down, which can be visualized on a graph.
  • ⏫⏬ **Direction of Concavity Change**: A curve that is increasing everywhere can still be concave up or down, and the direction of concavity can change even if the function value is always rising.
  • 📐 **Second Derivative Test**: The concavity of a function can be determined by the sign of the second derivative; positive implies concave up, and negative implies concave down.
  • 🔄 **Inflection Points**: An inflection point is where a function changes concavity, either from concave down to concave up or vice versa, and it is marked by a second derivative of zero.
  • ⚠️ **Not All Zero Derivatives Are Inflection Points**: A zero second derivative is necessary but not sufficient for an inflection point; the function's concavity must actually change.
  • 🔢 **Finding Inflection Points**: To find possible inflection points, set the second derivative to zero and solve for x, then test intervals around the solutions to confirm a change in concavity.
  • 📉 **Example Analysis**: The script provides several examples of functions, their derivatives, and how to determine intervals of concavity and locate inflection points.
  • 🌐 **Continuous Second Derivative**: For functions with a continuous second derivative, an inflection point will always have a second derivative of zero, though the converse is not always true.
Q & A

  • What are the two main types of lenses discussed in the video?

    -The two main types of lenses discussed are convex lenses, which are thicker in the middle and bulge outward, and concave lenses, which are thinner in the middle and curve inward.

  • How does the video help to remember the term 'concave'?

    -The video suggests imagining a very concave lens that might resemble a cave or a cliff side, using the visual association with 'cave' to remember the term 'concave'.

  • What does the term 'concave up' refer to in the context of a function?

    -In the context of a function, 'concave up' refers to an interval where the function's curve is curving upward, resembling a bowl shape that could hold water.

  • How is the term 'concave down' different from 'concave up'?

    -The term 'concave down' refers to an interval where the function's curve is curving downward, similar to a bowl shape but inverted.

  • What is the mathematical definition of a function being concave up?

    -A function is defined as concave up if its second derivative is positive.

  • What is the mathematical definition of a function being concave down?

    -A function is defined as concave down if its second derivative is negative.

  • What is an inflection point in the context of a function?

    -An inflection point is a point on the graph of a function where the concavity changes. It is where the function goes from being concave down to concave up or vice versa.

  • What is the relationship between an inflection point and the second derivative of a function?

    -At an inflection point, the second derivative of a function with a continuous second derivative is always zero. However, not every zero second derivative is an inflection point.

  • How does the video use the concept of rainwater to illustrate concavity?

    -The video uses the concept of rainwater to illustrate concavity by suggesting that a concave up section of a curve could hold rainwater, while a concave down section would not be able to.

  • What is the significance of finding points where the second derivative is zero?

    -Finding points where the second derivative is zero is significant because these points are potential inflection points. However, they must be further evaluated to confirm if they are indeed inflection points by checking the concavity on either side of the point.

  • How does the video demonstrate the concept of a function not having an inflection point?

    -The video demonstrates this by showing the function of the natural logarithm, which is concave down everywhere within its domain. Since there are no points where the second derivative is zero, there are no inflection points.

  • What is a decoy in the context of finding inflection points?

    -A decoy in the context of finding inflection points is a point where the second derivative is zero but is not an inflection point because the concavity does not change on either side of that point.

Outlines
00:00
🔍 Introduction to Concavity and Inflection Points

This paragraph introduces the concepts of concavity and inflection points, which are important in the study of optics and lenses. The distinction between convex and concave lenses is explained using visual analogies, and the mathematical definitions of concave up and down are discussed. The paragraph also explains how the curvature of a graph can indicate whether a function is concave up or down, and it uses the idea of a graph holding rainwater to illustrate this concept. The formal definitions of concavity are given in terms of the second derivative being positive (concave up) or negative (concave down).

05:04
📈 Identifying Concavity and Inflection Points

The second paragraph delves into the process of identifying intervals of concavity and inflection points for a given function. It defines an inflection point as the point where a function changes concavity, either from concave down to concave up or vice versa. The relationship between inflection points and the second derivative being zero is explored, with the caveat that not every zero second derivative is an inflection point. The paragraph provides an example of finding inflection points by setting the second derivative to zero and then checking the concavity on either side of the potential inflection points to confirm the switch in concavity.

10:05
🔢 Analyzing Functions for Concavity and Inflection Points

This paragraph presents multiple examples of functions and demonstrates how to analyze them for concavity and inflection points. It involves calculating the first and second derivatives and then using these to identify intervals of concavity and potential inflection points. The examples illustrate how to determine whether a point with a zero second derivative is an inflection point by evaluating the concavity on either side of the point. The paragraph also clarifies that a zero second derivative does not always indicate an inflection point if the concavity does not change.

15:05
🌐 No Inflection Points in Certain Functions

The final paragraph discusses the natural log function and why it does not have any inflection points. It explains that since the second derivative of the natural log function is always negative, there are no points where the second derivative is zero, and thus no inflection points. The paragraph reinforces the idea that the absence of a zero second derivative indicates a consistent concavity across the function's domain. The natural log function is shown to be concave down everywhere, which is why it lacks inflection points.

Mindmap
Keywords
💡Concavity
Concavity refers to the curvature of a function or curve. In the context of the video, a curve is said to be concave up if it curves upward like the exterior of a bowl, which could theoretically hold water. Conversely, a curve is concave down if it curves inward like the interior of a bowl. The concept is central to understanding the behavior of functions and is illustrated through various examples in the video.
💡Convex Lenses
Convex lenses are a type of lens that bulges outward, like a magnifying glass. They are mentioned in the video as an example to contrast with concave lenses. Convex lenses are important in the field of optics, particularly in the construction of lenses for devices like telescopes and eyeglasses.
💡Concave Lenses
Concave lenses are thinner at the center than at the edges and cause light to diverge. They are used in the video to introduce the concept of concavity in a physical context, which is then related to the mathematical discussion of concave functions. Concave lenses are also used in corrective lenses for myopia (nearsightedness).
💡Second Derivative
The second derivative of a function is the derivative of the first derivative. It provides information about the concavity of a function. If the second derivative is positive, the function is concave up, and if it's negative, the function is concave down. In the video, the second derivative is used to determine the intervals of concavity and to identify inflection points.
💡Inflection Points
An inflection point is a point on a curve where the concavity changes. It's where a function transitions from being concave up to concave down or vice versa. In the video, the concept is introduced as a critical aspect of analyzing the behavior of functions, and it's demonstrated how to find these points by looking for where the second derivative is zero.
💡Optics
Optics is the branch of physics that studies the behavior and properties of light, including its reflection, refraction, and the use of lenses to manipulate these properties. The video begins with a reference to optics, particularly in the context of lenses, to draw an analogy with the mathematical concept of concavity.
💡Interval
In mathematics, an interval refers to a continuous range of values, which can be open, closed, or half-open/half-closed. The video discusses identifying intervals over which a function is concave up or concave down, which is crucial for understanding the overall shape and behavior of the function.
💡Derivative
A derivative in calculus represents the rate at which a function changes with respect to a variable. The first derivative gives the slope of the tangent line to the function at a point, while higher-order derivatives provide additional information about the function's behavior. In the video, derivatives are used to analyze the concavity and find inflection points of functions.
💡Continuous Second Derivative
A function having a continuous second derivative means that the second derivative is defined and does not have any abrupt changes or 'jumps' throughout its domain. In the video, it is mentioned that if a function has a continuous second derivative, an inflection point occurs where the second derivative is zero.
💡Rain Water Analogy
The rain water analogy is a mnemonic used in the video to help viewers visualize whether a curve is concave up or down. A curve is concave up if it is shaped like a surface that could collect rain water, and concave down if it is shaped like a surface that would allow water to drain away.
💡Decoy
In the context of the video, a decoy refers to a point where the second derivative is zero but is not an inflection point. This occurs when the concavity does not change at that point; the function remains concave up or down on both sides of the point. The term is used to highlight the distinction between points of zero second derivative and actual inflection points.
Highlights

The video discusses the concepts of concavity and inflection points in the context of both physics (optics and lenses) and mathematics.

Differentiates between convex and concave lenses, with a mnemonic to remember their shapes.

Introduces the mathematical definition of concavity, relating it to the orientation of a curve or function.

Uses the analogy of holding rainwater to describe concave up curves on a graph.

Identifies the interval from zero to positive infinity as concave up for the given blue curve example.

Explains that the interval from negative infinity to zero is concave down for the same curve.

Discusses the difficulty in identifying concavity in a curve that is increasing everywhere, like the red curve example.

Formal definitions are provided: a function is concave up if the second derivative is positive, and concave down if it's negative.

An inflection point is defined as the point where a function changes concavity, marked by a second derivative of zero.

Not every zero second derivative point is an inflection point, emphasizing the need for concavity change.

Demonstrates how to find intervals of concavity and potential inflection points using derivatives.

Provides an example using the function y = (1/2)x^4 - x^2 to illustrate finding inflection points and concavity intervals.

Shows that a zero second derivative at x = 0 does not always indicate an inflection point, using the curve y = x^3 - x as an example.

Explains that the natural logarithm function has no inflection points and is concave down everywhere within its domain.

The video uses visual examples of curves to help understand the concepts of concavity and inflection points.

Highlights the importance of the second derivative in determining concavity and identifying inflection points.

The presenter uses a step-by-step approach to analyze different functions and their concavity properties.

The video concludes by reinforcing the understanding of concavity and inflection points with practical mathematical examples.

Transcripts

Browse More Related Video

Concavity, Inflection Points, and Second Derivative

Finding Concavity and Inflection Points

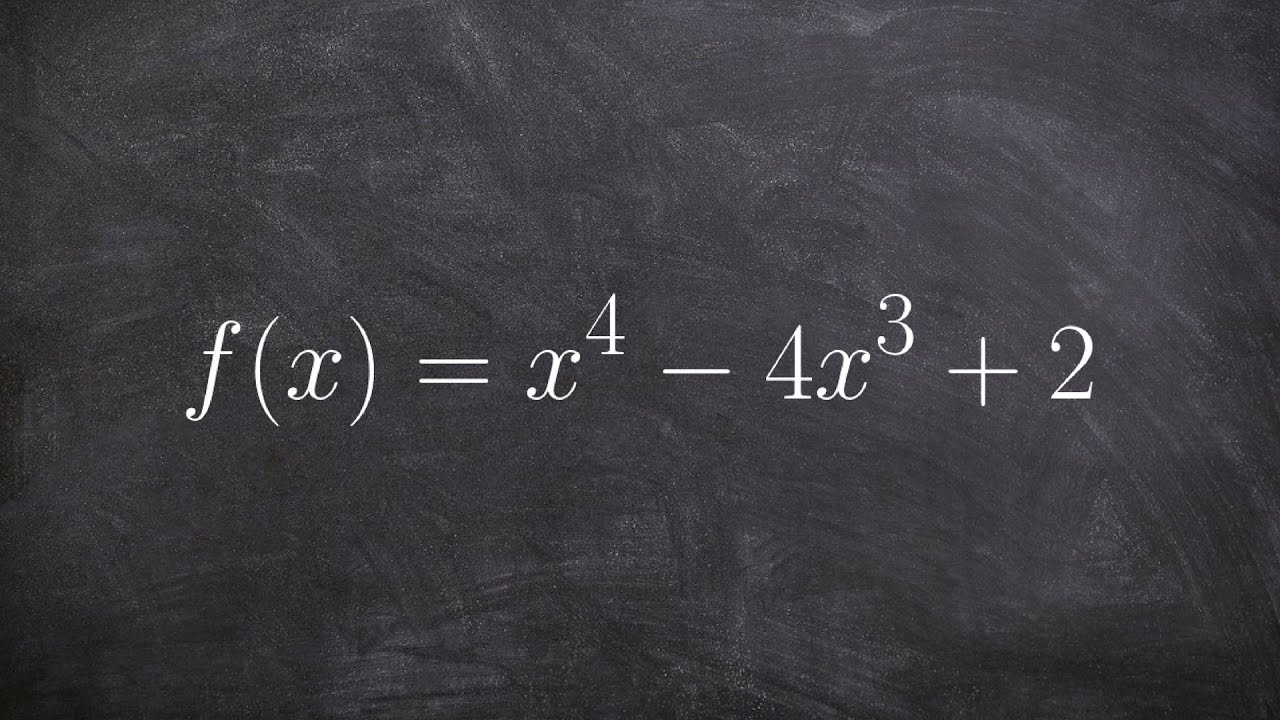
Learn how to determine concavity and point of inflection AP style

MATH1325 Lecture 10 2 - Concavity & Points of Inflection

Business Calculus - Math 1329 - Section 3.2 - Concavity and Points of Inflection

Calculus 1: Concavity Examples

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
ConcavityInflection PointsOpticsLensesMathematicsEducationalPhysicsDerivativesGraph AnalysisFunction Curves