Compound Interest
TLDRThis educational video script explores compound interest calculations with various examples. It demonstrates how to calculate the future value of an investment using the formula A = P(1 + r/n)^(nt), where P is the principal, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the time in years. The script illustrates the impact of time on investment growth, comparing 10-year and 20-year investment periods and showing the effect of different compounding frequencies. It concludes with a formula to determine how long it takes for an investment to double, using the natural logarithm, and introduces the Rule of 72 as a quick approximation tool.
Takeaways
- 📈 The video discusses compound interest calculations and their impact on investment growth over time.
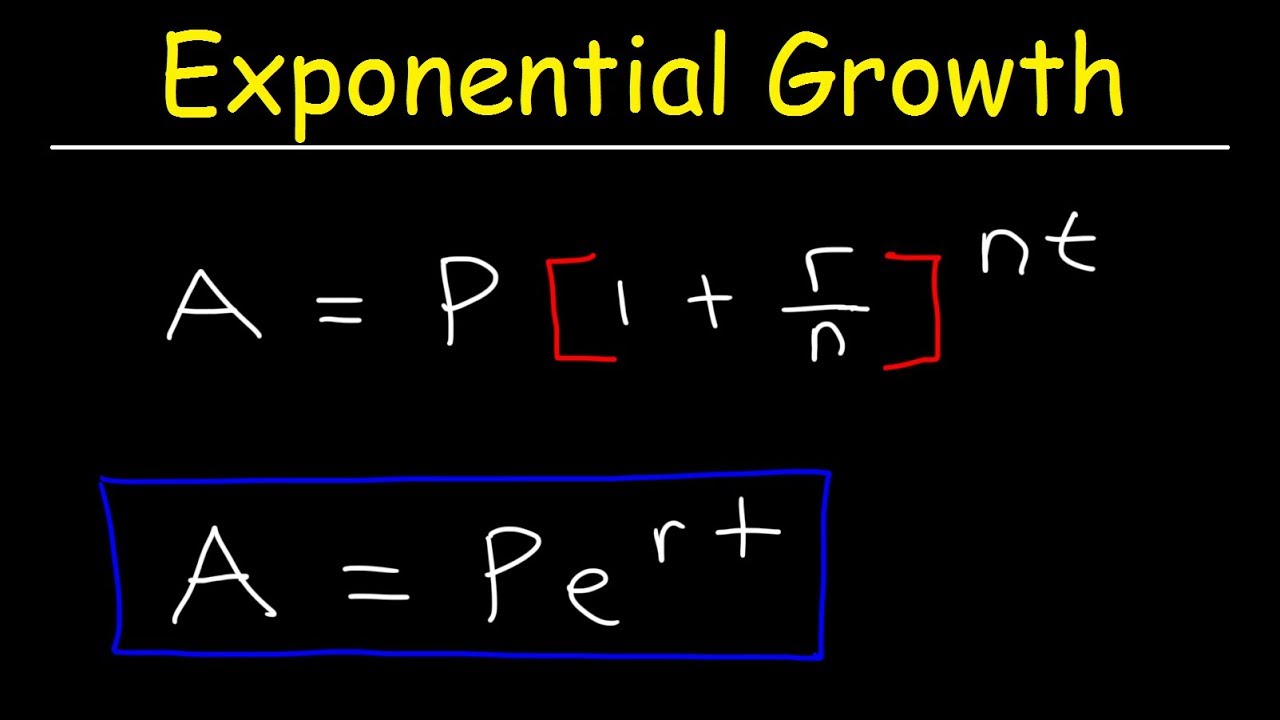
- 💡 The formula for calculating the final account value is principal * (1 + (interest rate / number of times interest is compounded per year)) ^ (number of years * number of times interest is compounded per year).
- 🔢 For an account that compounds annually, the value after 10 years of a $1,000 investment at 9% interest is $2,367.36.
- 🕒 The importance of time in investing is highlighted, as the same investment grows to $5,604.41 after 20 years, demonstrating the power of compounding over a longer period.
- 📊 The growth from $1,000 to $2,367.36 in 10 years shows a gain of $1,367.36, while the gain from $1,000 to $5,604.41 in 20 years is $4,604.41, illustrating the exponential nature of compound interest.
- 🏦 In the second example, Sam's $5,000 investment at 10% interest compounded quarterly for 20 years results in a value of $36,047.84.
- 📈 When the same investment is compounded monthly instead of quarterly, the value increases to $36,640.37, showing the benefit of more frequent compounding.
- 📚 The video explains that more frequent compounding results in slightly higher returns, as seen in the comparison between quarterly and monthly compounding.
- 🤔 The final problem involves calculating the time it takes for an investment to double in value using the formula: time to double = ln(2) / ln(1 + interest rate).
- 🔑 The Rule of 72 provides a quick approximation for the time it takes to double an investment, calculated as 72 divided by the interest rate as a percentage.
- 📝 The video concludes with the example of Megan's $10,000 investment at 6% interest, which takes approximately 11.896 years to double, using the natural log formula, or about 12 years using the Rule of 72.
Q & A
What is the formula used to calculate the final account value with compound interest?
-The formula used is A = P(1 + r/n)^(nt), where A is the final account value, P is the principal amount, r is the annual interest rate as a decimal, n is the number of times interest is compounded per year, and t is the time in years.
What is the annual interest rate for Luke's investment as a decimal?
-The annual interest rate for Luke's investment is 9 percent, which as a decimal is 0.09.
If the account is compounded annually, what is the value of n in the compound interest formula?
-If the account is compounded annually, the value of n, which represents the number of times interest is compounded per year, is 1.
What will be the value of Luke's account after 10 years with an annual compounding?
-After 10 years, with an annual compounding, the value of Luke's account will be $2,367.36.
How much interest did Luke earn on his initial investment after 10 years?
-Luke earned $1,367.36 in interest on his initial investment of $1,000 after 10 years.
What is the value of Sam's account after 20 years with quarterly compounding?
-After 20 years with quarterly compounding, the value of Sam's account will be $36,047.84.
How does the frequency of compounding affect the total return on investment?
-The more frequently interest is compounded, the greater the total return on investment, as it allows for the interest to be earned on previously earned interest more often.
What is the difference in the account value when interest is compounded quarterly versus monthly for Sam's 20-year investment?
-When interest is compounded monthly instead of quarterly, Sam's account value increases by approximately $600, from $36,047.84 to $36,640.37.
What is the purpose of taking the natural log in Megan's investment problem?
-Taking the natural log is used to isolate the variable t (time) in the compound interest formula, allowing us to solve for the number of years it takes for the investment to double.
How many years will it take for Megan's investment to double in value at an annual interest rate of 6%?
-It will take approximately 11.896 years for Megan's investment to double in value at an annual interest rate of 6%.
What is the Rule of 72 and how does it estimate the time to double an investment?
-The Rule of 72 is a simplified method to estimate the time it takes for an investment to double. It states that the time to double is equal to 72 divided by the annual interest rate as a percentage. For an interest rate of 6%, it estimates approximately 12 years to double the investment.
Outlines
💼 Compound Interest Calculation
This paragraph delves into the concept of compound interest, using Luke's investment as an example. Luke deposits $1,000 in an account with a 9% annual interest rate. The formula for calculating the final account value is given as A = P(1 + r/n)^(nt), where P is the principal, r is the interest rate in decimal form, n is the number of times interest is compounded per year, and t is the time in years. Assuming annual compounding (n=1), the account value after 10 years is calculated to be $2,367.36. Extending the time to 20 years, the value grows to $5,604.41, illustrating the power of time in investments. The paragraph emphasizes the importance of time in investment growth, showing that the longer the investment period, the greater the returns.
📈 Impact of Compounding Frequency on Investment Growth
The second paragraph explores how the frequency of interest compounding affects the growth of an investment. Sam invests $5,000 at a 10% annual interest rate for 20 years. The difference in compounding frequency—quarterly (n=4) and monthly (n=12)—is highlighted. For quarterly compounding, the investment formula is applied with n=4, resulting in a future value of $36,047.84. When interest is compounded monthly, the value increases slightly to $36,640.37, showing that more frequent compounding leads to higher returns. The paragraph concludes by noting that while the difference may seem small, it can be significant over many years.
📊 Time to Double Investment Using the Rule of 72
The final paragraph focuses on the time it takes for an investment to double in value, using Megan's $10,000 annuity with a 6% annual interest rate as an example. The formula for calculating the doubling time is derived from the compound interest formula, leading to a natural logarithm-based calculation. The time it takes for Megan's investment to double is found to be approximately 11.896 years. The paragraph also introduces the Rule of 72 as a quick approximation method, which estimates the doubling time to be around 12 years by dividing 72 by the interest rate (6%). This rule provides a simple way to estimate the doubling time without complex calculations.
Mindmap
Keywords
💡Compound Interest
💡Principal
💡Interest Rate
💡Annual Basis
💡Time Value of Money
💡Quarterly
💡Monthly
💡Annuity
💡Natural Logarithm
💡Rule of 72
Highlights
Introduction to solving compound interest problems.
Explanation of the compound interest formula: A = P(1 + r/n)^(nt).
Definition of variables: A (final value), P (principal), r (interest rate), n (compounding frequency), t (time).
Example calculation: Luke's account with $1000 at 9% annual interest.
Conversion of 9% interest rate to decimal form (0.09).
Determining n as 1 for annual compounding.
Calculation of account value after 10 years: $2,367.36.
Calculation of account value after 20 years: $5,604.41.
Analysis of investment growth over time, emphasizing the importance of time in investing.
Investment growth comparison: 10 years vs. 20 years.
Example of Sam's investment: $5,000 at 10% annual interest, compounded quarterly.
Calculation for quarterly compounding: n = 4, r = 0.10, t = 20 years.
Result of Sam's investment after 20 years with quarterly compounding: $36,047.84.
Comparison of different compounding frequencies: quarterly vs. monthly.
Impact of compounding frequency on investment returns.
Megan's investment example: $10,000 in an annuity with 6% annual interest.
Doubling time calculation formula using natural logarithms.
Application of the doubling time formula to Megan's investment.
Calculation of doubling time for Megan's investment: 11.896 years.
Introduction to the Rule of 72 as an approximation for doubling time.
Comparison of the doubling time formula result with the Rule of 72 estimate.
Transcripts
Browse More Related Video

Interest Compounded Continuously

Review of Compound Interest (Precalculus - College Algebra 65)

Compound Interest Formula Explained, Investment, Monthly & Continuously, Word Problems, Algebra

Continuous Money Flow: Future Value with increasing rate of growth
Compound Interest & Population Growth Word Problems - Logarithms

Compound interest and e (part 4) | Exponential and logarithmic functions | Algebra II | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: