Interest Compounded Continuously
TLDRThis tutorial explains how to calculate the future value of an investment with continuously compounded interest and the time it takes to double the investment. The formula used is \( a = pe^{rt} \), where \( a \) is the future value, \( p \) is the principal, \( r \) is the annual interest rate (as a decimal), \( t \) is the time in years, and \( e \) is the base of the natural logarithm (approximately 2.71828). The example provided involves a $10,000 investment growing at 9% annually, which would be worth $24,596.03 after 10 years. To find the doubling time, the tutorial rearranges the formula and uses the natural log, showing that the investment would double in approximately 7.7 years. The Rule of 72 is also introduced as a quick estimation method, which approximates the doubling time to be around 8 years.
Takeaways
- 🧮 The tutorial discusses solving problems involving continuously compounded interest.
- 💰 Kim invests $10,000 in a mutual fund that grows at an average annual rate of 9%.
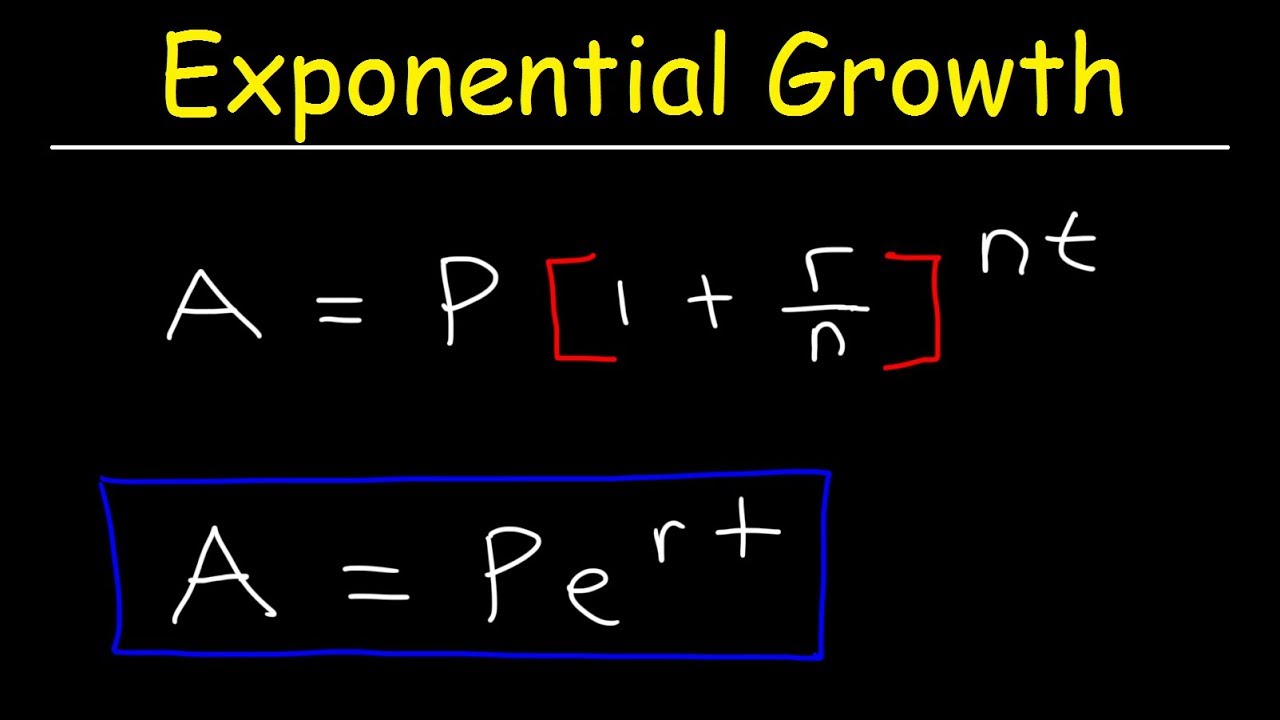
- 📚 To find the future value of the account, use the formula \( a = pe^{rt} \) where \( a \) is the future value, \( p \) is the principal, \( r \) is the interest rate as a decimal, and \( t \) is the time in years.
- 🔢 The value of \( e \) is approximately 2.7182818, which is used in the formula for continuously compounded interest.
- 📈 After 10 years, Kim's investment will be worth $24,596.03, calculated using the formula with \( r = 0.09 \) and \( t = 10 \).
- ⏱ The tutorial then moves on to determine how long it will take for Kim's investment to double.
- 🔄 To solve for time, the formula is rearranged and the natural logarithm is used to isolate \( t \).
- 📉 The time it takes to double the investment is given by \( \frac{\ln(2)}{r} \), where \( r \) is the interest rate as a decimal.
- 📊 Plugging in the values, the investment will double in approximately 7.7 years with a 9% interest rate.
- 🎯 An alternative method to estimate the doubling time is using the Rule of 72, which approximates the doubling time to 8 years for a 9% interest rate.
- 📝 The video concludes by summarizing the methods to solve problems related to continuously compounded interest.
Q & A
What formula is used to calculate the future value of an account with continuously compounded interest?
-The formula used is A = P * e^(rt), where A is the future value of the account, P is the principal amount, r is the interest rate as a decimal, t is the time in years, and e is the mathematical constant approximately equal to 2.7182818.
What is the principal amount invested in the mutual fund in the given problem?
-The principal amount invested is $10,000.
How do you convert the interest rate from a percentage to a decimal?
-To convert the interest rate from a percentage to a decimal, divide the percentage by 100. For example, 9% becomes 0.09.
What is the value of the mutual fund after 10 years with a 9% annual growth rate compounded continuously?
-The value of the mutual fund after 10 years is $24,596.03.
How do you solve for the time it takes for an investment to double with continuously compounded interest?
-To solve for the time (t) it takes for an investment to double, use the formula t = ln(2) / r, where ln is the natural logarithm and r is the interest rate as a decimal.
What is the natural logarithm of e (ln(e))?
-The natural logarithm of e (ln(e)) is equal to 1.
Using the given problem, how long will it take for Kim's investment to double at a 9% annual growth rate?
-It will take approximately 7.7 years for Kim's investment to double at a 9% annual growth rate.
What is the rule of 72, and how is it used to estimate the doubling time of an investment?
-The rule of 72 is a simple way to estimate the time it takes for an investment to double. It states that the doubling time is approximately 72 divided by the annual interest rate as a percentage. For example, with a 9% interest rate, the doubling time is approximately 72 / 9 = 8 years.
Why is the rule of 72 a good approximation for estimating the doubling time of an investment?
-The rule of 72 is a good approximation because it provides a quick and simple method to estimate the doubling time without complex calculations. It works well for interest rates commonly seen in financial scenarios.
What is the approximate value of e, and why is it important in the context of continuously compounded interest?
-The approximate value of e is 2.7182818. It is important in the context of continuously compounded interest because it is the base of the natural logarithm used in the formula A = P * e^(rt), which calculates the future value of an account with continuously compounded interest.
Outlines
📈 Calculating the Future Value of an Investment with Continuous Compounding
This paragraph introduces a tutorial on solving problems involving continuously compounded interest. Kim invests $10,000 in a mutual fund with an average annual growth rate of 9%. To find the account's value after 10 years, the formula A = pe^(rt) is used, where A is the future value, p is the principal ($10,000), r is the interest rate (0.09), t is the time (10 years), and e is the base of the natural logarithm (approximately 2.71828). The calculation results in a future value of $24,596.03. The paragraph also discusses how to determine the time it takes for an investment to double, using the rearranged formula and taking the natural logarithm of both sides to solve for t, which in this case is 7.7 years.
🔍 Estimating Doubling Time with the Rule of 72
The second paragraph continues the discussion on investment growth, focusing on estimating the time it takes for an investment to double using the Rule of 72. Instead of using the continuous compounding formula, this rule provides a quick approximation by dividing 72 by the interest rate (9%), yielding an estimated doubling time of 8 years. This is a close approximation to the 7.7 years calculated previously, demonstrating the rule's utility for quick estimations in finance.
Mindmap
Keywords
💡Continuously Compounded Interest
💡Principal (P)
💡Interest Rate (r)
💡Time (t)
💡Euler's Number (e)
💡Future Value (A)
💡Natural Logarithm (ln)
💡Doubling Time
💡Rule of 72
💡Mutual Fund
Highlights
The tutorial discusses solving problems involving continuously compounded interest.
Kim invests $10,000 in a mutual fund with a 9% annual growth rate.
The future value of the account is calculated using the formula a = pe^(rt).
The value 'e' is approximately 2.7182818.
The principal (p) is $10,000, the interest rate (r) is 0.09, and time (t) is 10 years.
The account's value after 10 years will be $24,596.03.
The tutorial moves on to calculate how long it takes for an investment to double.
The formula is rearranged to solve for time (t) when the investment doubles.
The natural log is used to isolate t in the equation.
The time to double the investment is ln(2) divided by the interest rate.
The account will double in value after approximately 7.7 years.
The Rule of 72 provides an estimation for the doubling time.
Using the Rule of 72, the investment will double in about 8 years.
The approximation of 7.7 years rounds to 8 years, aligning with the Rule of 72.
The tutorial concludes by summarizing the methods for solving continuous compound interest problems.
Transcripts
Browse More Related Video

Compound Interest

Continuous Money Flow: Future Value with increasing rate of growth

Compound interest and e (part 4) | Exponential and logarithmic functions | Algebra II | Khan Academy
Compound Interest & Population Growth Word Problems - Logarithms

Review of Compound Interest (Precalculus - College Algebra 65)

Continuous Money Flow: Finding Revenue Stream when Future Value is Known
5.0 / 5 (0 votes)
Thanks for rating: