Compound Interest Formula Explained, Investment, Monthly & Continuously, Word Problems, Algebra

The Organic Chemistry Tutor

7 Dec 201622:06

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script focuses on solving word problems using the compound interest formula. It introduces two key equations for calculating future investment values: one for standard compounding and another for continuous compounding. The script explains the variables involved, such as principal (p), annual interest rate (r), compounding frequency (n), and time (t). It then walks through several problems, demonstrating how to apply the formulas to determine future account balances or the initial deposits needed to reach financial goals. The examples illustrate the power of compound interest and emphasize the benefits of early saving and investing.

Takeaways

📚 The video discusses solving word problems using the compound interest formula, which is essential for understanding how savings grow over time.
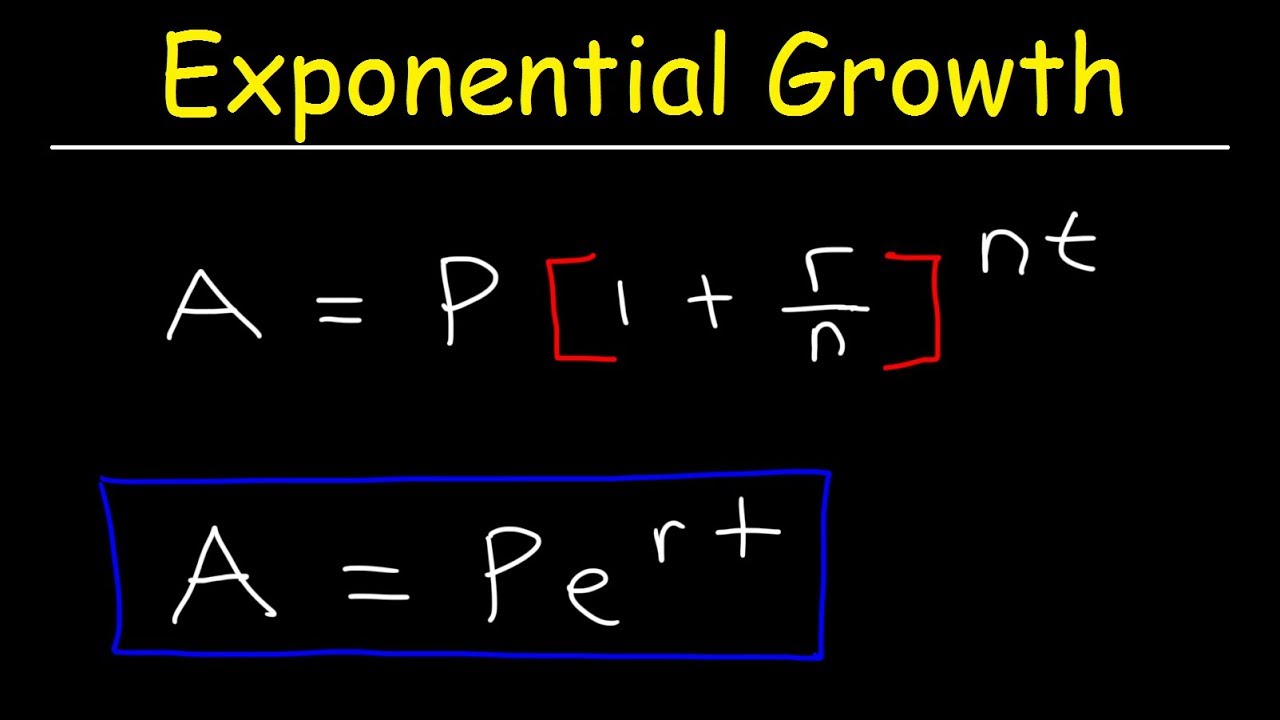
💰 The compound interest formula is A = P(1 + r/n)^(nt), where P is the principal amount, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the time in years.
📈 The future value (A) represents the amount that will be in the account after interest has been applied over a period of time, while the present value (P) is the initial deposit.
🔢 To use the formula, convert the annual interest rate (r) from a percentage to a decimal by dividing by 100, and determine the value of n based on how often interest is compounded.
🌐 For different compounding periods, n equals 12 for monthly, 52 for weekly, 365 for daily, 4 for quarterly, 2 for semi-annually, and 1 for annually.
🔑 There's an alternative formula for continuous compounding: A = Pe^(rt), which is used when the interest is compounded an infinite number of times per year.
🧐 The script provides examples to illustrate the calculations, such as calculating future savings based on different interest rates and compounding periods.
🏦 The importance of investing early is highlighted, as the power of compound interest allows even small investments to grow significantly over time.
📉 The script also covers how to calculate the amount needed to invest now to reach a future goal, using the compound interest formula in reverse.
⏳ The time it takes for an investment to grow to a certain amount is determined by factors such as the interest rate, compounding frequency, and the initial investment.
🤔 The video encourages viewers to pause and work on the problems themselves to better understand the concepts and calculations involved in compound interest.

Q & A

What are the two formulas discussed in the video for calculating compound interest?
-The two formulas discussed in the video for calculating compound interest are: 1) A = P(1 + r/n)^(nt), where P is the principal amount, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the time in years. 2) A = Pe^(rt), which is used when the interest is compounded continuously.
What does 'P' represent in the compound interest formula?
-'P' in the compound interest formula represents the principal, which is the initial amount of money deposited into an account or the starting value of an investment.
How do you convert an annual interest rate percentage to a decimal for use in the compound interest formula?
-To convert an annual interest rate percentage to a decimal, you divide the percentage by 100.
What is the value of 'n' if the interest is compounded monthly?
-'n' would be 12 if the interest is compounded monthly, as there are 12 months in a year.
What is the value of 'n' for different compounding periods such as weekly, daily, quarterly, semi-annually, and annually?
-The value of 'n' is 52 for weekly compounding, 365 for daily, 4 for quarterly, 2 for semi-annually, and 1 for annual compounding.
How is the time 't' represented in the compound interest formula?
-In the compound interest formula, 't' represents the time in years that the money is invested or the period over which the interest is compounded.
What is the significance of the number 'e' in the continuous compounding formula?
-In the continuous compounding formula, 'e' is the base of the natural logarithm, which is used to calculate compound interest when the interest is compounded an infinite number of times per year.
How much money will be in Susan's account after 40 years with an initial deposit of $20,000, an 8% annual interest rate, and monthly compounding?
-After 40 years, Susan's account will have approximately $485,794.79, calculated using the formula A = P(1 + r/n)^(nt) with P = $20,000, r = 0.08, n = 12, and t = 40.
How much should John deposit into his mutual fund to have $2 million for retirement in 45 years, given an average annual interest rate of 9.5% compounded quarterly?
-John should deposit approximately $29,249.96 into his mutual fund to reach his goal of $2 million in 45 years, using the formula A = P(1 + r/n)^(nt) with A = $2,000,000, r = 0.095, n = 4, and t = 45.
What annual interest rate does Sarah need to receive, compounded annually, to turn her $10,000 investment into $100,000 in 20 years?
-Sarah needs an annual interest rate of 12.2% to reach her goal of $100,000 in 20 years, starting with a $10,000 investment and using the formula A = P(1 + r/n)^(nt) with A = $100,000, P = $10,000, n = 1, and t = 20.
How many years will it take for Mary's $50,000 investment to reach $1 million at an 8.4% annual interest rate compounded semi-annually?
-It will take approximately 36.4 years for Mary's investment to grow to $1 million using the formula A = P(1 + r/n)^(nt) with A = $1,000,000, P = $50,000, r = 0.084, n = 2, and solving for t.
How much money will be in Julia's account after 30 years with an initial deposit of $100,000, a 7.2% annual interest rate, and continuous compounding?
-After 30 years, Julia's account will have approximately $167,113.77, calculated using the formula A = Pe^(rt) with P = $100,000, r = 0.072, and t = 30.
How much should Mark invest now in an account paying 12% interest compounded continuously to have $1.5 million in 50 years?
-Mark should invest approximately $3,718.13 now to have $1.5 million in 50 years, using the formula A = Pe^(rt) with A = $1,500,000, r = 0.12, t = 50, and solving for P.
How long will it take for John's $5 million investment to turn into $20 million at an 11% annual interest rate compounded continuously?
-It will take approximately 54.47 years for John's investment to grow to $20 million using the formula A = Pe^(rt) with A = $20,000,000, P = $5,000,000, r = 0.11, and solving for t.

Outlines

00:00

📈 Introduction to Compound Interest Formulas

In this video, we will work on solving word problems using the compound interest formula. There are two key equations to know. The first is A = P * (1 + (r / n))^(nt), where P is the principal amount, A is the future value, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the time in years. The second formula, A = P * e^(rt), is used for continuously compounded interest. The video explains how to convert interest rates to decimals, and how to determine n based on different compounding periods. The formulas are applied to solve several problems, demonstrating the impact of different compounding frequencies on the future value of investments.

05:01

💰 Calculating Future Value for Retirement

John aims to have $2 million for retirement in 45 years by investing in a mutual fund with an average annual interest rate of 9.5%, compounded quarterly. The formula A = P * (1 + (r / n))^(nt) is used to determine how much he should deposit now. By converting the interest rate to a decimal and dividing by the number of compounding periods, the future value of the investment is calculated. The necessary initial deposit amount is found to be approximately $29,249.96. This illustrates the benefits of starting investments early to maximize compound interest.

10:01

📊 Determining Required Interest Rate

Sarah wants to turn her $10,000 investment into $100,000 in 20 years, compounded annually. To find the required annual interest rate, the formula A = P * (1 + (r / n))^(nt) is used. By solving for r, it is determined that she needs an interest rate of 12.2% per year. This example highlights how understanding and manipulating the compound interest formula can help set realistic financial goals and find appropriate investment opportunities.

15:02

💵 Calculating Investment Duration

Mary invests $50,000 in an index annuity averaging an annual interest rate of 8.4%, compounded semi-annually. To determine how long it will take for her investment to reach $1 million, the formula A = P * (1 + (r / n))^(nt) is used. By solving for t using logarithms, it is found that it will take approximately 36.4 years. This problem demonstrates the powerful effect of compound interest over long periods, emphasizing the importance of starting investments early.

20:03

🔢 Continuously Compounded Interest Calculation

Julia invests $100,000 in an account with a 7.2% interest rate, compounded continuously. Using the formula A = P * e^(rt), the future value of her investment after 30 years is calculated to be approximately $867,113.77. This example shows how continuously compounded interest can significantly grow an investment over time.

🔄 Small Investment with High Returns

Mark wants to have $1.5 million in 50 years by investing in an account with a 12% interest rate, compounded continuously. By applying the formula A = P * e^(rt), it is determined that he should invest about $3,718.13 now. This problem illustrates how a small initial investment can grow substantially over a long period due to the high interest rate and continuous compounding.

📅 Calculating Investment Time Frame

John invests $5,000 in an account with an 11% interest rate, compounded continuously, and wants to know how long it will take to grow to $2 million. Using the formula A = P * e^(rt) and solving for t with natural logarithms, it is found that it will take approximately 54.47 years. This problem underscores the importance of early investment to leverage the power of compound interest over time.

Mindmap

Keywords

💡Compound Interest

Compound interest is the interest on a loan or deposit calculated based on both the initial principal and the accumulated interest from previous periods. It is central to the video's theme, as it is the method used to calculate the growth of investments over time. The script explains that compound interest can be compounded at different intervals, such as monthly, quarterly, or continuously, which affects the final amount accumulated.

💡Principal

The principal refers to the initial amount of money deposited into a savings account or invested in a financial product. In the context of the video, the principal is the starting point for calculating future value through compound interest. The script uses examples like Susan's $20,000 deposit to illustrate how the principal grows over time with interest.

💡Future Value (A)

Future value, denoted as 'A' in the script, is the amount that will be available in the future after the principal has been compounded over a certain period. It is a key concept in the video, showing the potential growth of an investment. For example, the script calculates the future value of Susan's investment after 40 years to demonstrate the power of compound interest.

💡Annual Interest Rate (R)

The annual interest rate, or 'r', is the percentage of the principal paid annually by a bank or investment as interest. It is a crucial factor in compound interest calculations. The script explains that this rate must be converted into a decimal for calculations and varies depending on the financial product.

💡Compounding Frequency (N)

Compounding frequency, represented by 'n', is the number of times interest is compounded per year. It can be annually, semi-annually, quarterly, monthly, weekly, daily, or continuously. The script discusses different values of 'n' for various compounding periods, which affects the calculation of compound interest.

💡Time (T)

Time, or 't', is the number of years the money is invested or the period over which compound interest is calculated. It is essential in determining the final amount of an investment. The script uses time as a variable in the compound interest formula to show how long an investment needs to grow to reach a certain value.

💡Continuous Compounding

Continuous compounding is a method of calculating interest where the interest is added an infinite number of times per year. The script specifies that when interest is compounded continuously, a different formula involving 'e' (Euler's number) is used, as opposed to the standard compound interest formula.

💡Euler's Number (e)

Euler's number, or 'e', is a fundamental mathematical constant used in the formula for continuous compounding. It is the base of the natural logarithm and is approximately equal to 2.71828. The script mentions 'e' as part of the formula for continuous compounding, where it is raised to the power of 'rt' to calculate future value.

💡Investment Growth

Investment growth refers to the increase in the value of an investment over time due to compound interest. The video's script provides several examples of investment growth, such as John's plan to have $2 million for retirement or Sarah's goal to turn $10,000 into $100,000, illustrating the impact of compound interest on investment growth.

💡Retirement Savings

Retirement savings is the money set aside for use after retirement. It is a key application of the concepts discussed in the video, such as compound interest and future value. The script gives an example of John wanting to have $2 million for retirement, which is calculated using the principles of compound interest.

💡Interest Rate Conversion

Interest rate conversion is the process of converting a percentage interest rate into a decimal for use in mathematical calculations. The script explains that to use the annual interest rate in formulas, it must be divided by 100 to convert from a percentage to a decimal, which is a necessary step in calculating compound interest.

💡Mutual Fund

A mutual fund is a type of investment vehicle consisting of a portfolio of stocks, bonds, or other securities. The script mentions a mutual fund as an example of an investment option that pays an average annual interest rate, which can be compounded to grow an investment over time.

💡Index Annuities

Index annuities are a type of insurance product that offers a fixed rate of interest and is often tied to the performance of a specific market index. The script uses an example of Mary investing in an index annuity to illustrate how compound interest can be used to reach a financial goal over a certain period.

💡Logarithms

Logarithms are mathematical operations used to solve for exponents in equations. The script mentions using logarithms to solve for 't' in the compound interest formula when determining how long it will take for an investment to reach a certain value.

Highlights

Introduction to compound interest formula and its two key equations.

Explanation of the variables in the first compound interest formula: A = P(1 + r/n)^(nt).

Description of principal (P) as the initial amount deposited.

Future value (A) represents the amount in the account after interest accrual.

Annual interest rate (r) needs to be converted to a decimal.

Number of compounding periods per year (n) varies based on the compounding frequency.

Second compound interest formula: A = Pe^(rt) used for continuous compounding.

Explanation of 'e' as the base of the natural logarithm.

Use the first formula for periodic compounding and the second for continuous compounding.

Example problem: calculating future value with monthly compounding over 40 years.

Example problem: determining the initial deposit needed for a future goal with quarterly compounding.

Example problem: calculating required interest rate for achieving a future goal with annual compounding.

Example problem: finding the time needed to reach a future value with semi-annual compounding.

Example problem: calculating future value with continuous compounding over 30 years.

Example problem: determining the initial deposit needed for a future goal with continuous compounding.

Example problem: finding the time needed to reach a future value with continuous compounding.

Emphasis on the importance of starting to save early to maximize compound interest benefits.

Recommendation of mutual funds and index annuities for higher interest rates.

Transcripts

Browse More Related Video

Review of Compound Interest (Precalculus - College Algebra 65)

Compound Interest

Compound Interest & Population Growth Word Problems - Logarithms

Continuous Money Flow: Future Value with increasing rate of growth

Compound interest and e (part 3) | Exponential and logarithmic functions | Algebra II | Khan Academy

Interest (part 2) | Interest and debt | Finance & Capital Markets | Khan Academy

Related Tags

Compound Interest Savings Growth Investment Strategies Financial Planning Retirement Goals Interest Rates Continuous Compounding Semi-Annual Compounding Money Management Future Value