Compound interest and e (part 4) | Exponential and logarithmic functions | Algebra II | Khan Academy
TLDRThis educational video script explains the concept of continuously compounded interest in a clear and engaging manner. It begins with a simple scenario of borrowing a principal amount 'P' at an interest rate 'r', compounded continuously over a year, resulting in an amount of 'Pe^r'. The script then extends this to multiple years, deriving the formula 'Pe^(rt)' for the amount owed after 't' years. Practical examples are given, including calculating the future value of a $1,000 loan at a 25% interest rate over three years, and solving for the interest rate given the final amount owed. The script emphasizes the exponential growth of continuously compounded interest and encourages viewers to understand the underlying principles and formulas.
Takeaways
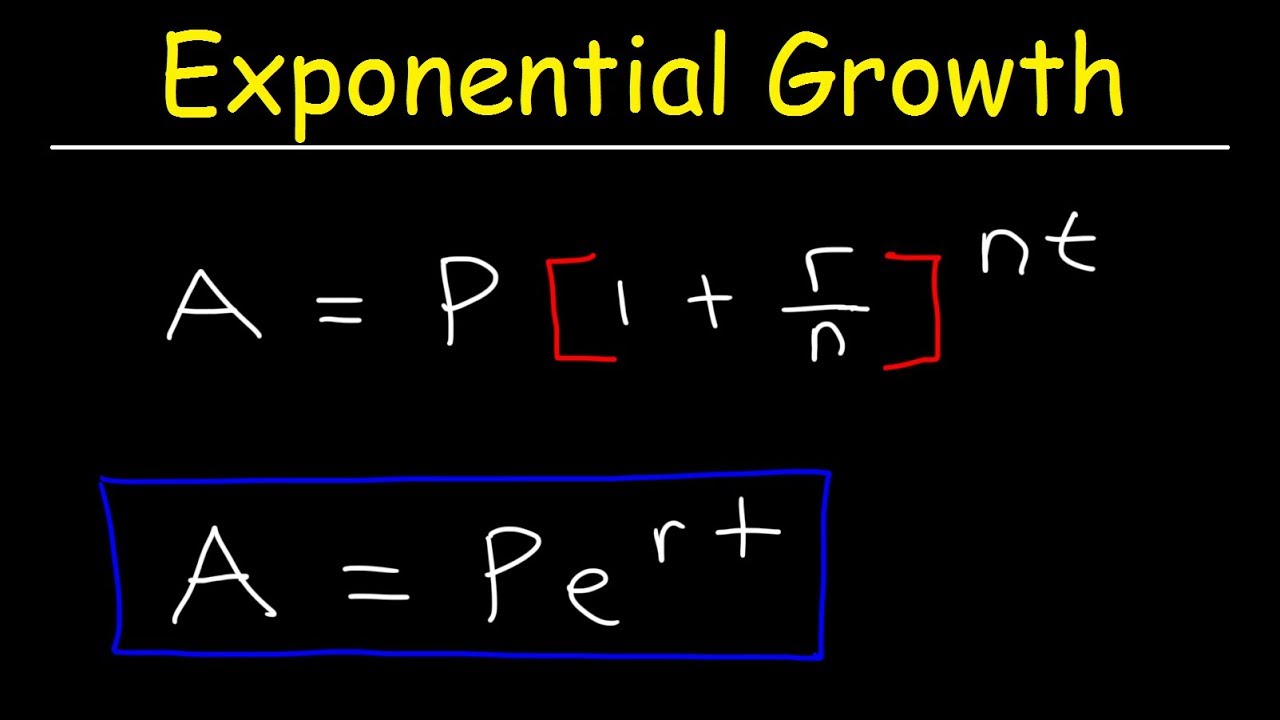
- 🧮 The formula for continuously compounded interest is \( P \cdot e^{rt} \), where \( P \) is the principal amount, \( r \) is the annual interest rate, and \( t \) is the time in years.
- 📈 After one year of continuous compounding, the amount owed is \( P \cdot e^r \), which is the principal multiplied by \( e \) raised to the power of the interest rate.
- 🔄 For each subsequent year, the new principal is the amount owed from the previous year, and this becomes the base for further compounding.
- 💰 If you borrow $1,000 at a 25% annual interest rate and it's continuously compounded for three years, you would owe $2,117 at the end of the period.
- 📚 The concept of continuous compounding is important to understand as it can lead to significant growth in the amount owed over time.
- 🔢 The power of compounding interest is demonstrated when comparing simple interest to continuous compounding, with the latter growing much faster.
- 📉 To find the original interest rate when given the final amount and time, you can use the formula \( e^{10r} = \frac{\text{Final Amount}}{\text{Principal}} \) and solve for \( r \).
- 🔑 Using logarithms, specifically the natural logarithm (LN), is a method to solve for the interest rate in continuous compounding scenarios.
- 📊 Excel can be used to calculate the final amount owed with continuous compounding by using the EXP function for \( e^x \) and LN for the natural logarithm.
- 📘 Continuous compounding is a fundamental concept in finance and is essential for anyone looking to understand the growth of investments or loans over time.
- 🔬 The script encourages viewers to practice with numbers and review logarithm concepts to gain a deeper understanding of continuous compounding interest.
Q & A
What is the formula for calculating the amount owed after continuously compounding interest for one year?
-The formula is Pe^(rt), where P is the principal amount borrowed, r is the annual interest rate (expressed as a decimal), and t is the time in years.
How does the amount owed change if the loan is for two years instead of one?
-If the loan is for two years, the amount owed becomes Pe^(2r), as the new principal after the first year compounds for another year.
What is the significance of the number e in the context of continuously compounding interest?
-The number e (approximately 2.71828) is the base of the natural logarithm and is used in the formula for continuous compounding because it represents the limit of (1 + 1/n)^n as n approaches infinity.
How much would you owe if you borrowed $1,000 at an annual interest rate of 25% for three years with continuous compounding?
-Using the formula Pe^(rt), you would owe $1,000 * e^(0.25*3), which equals approximately $2,117.
What is the Excel function used to calculate e to a power?
-In Excel, the function to calculate e to a power is 'EXP'. For example, to calculate e to the power of 0.75, you would use 'EXP(0.75)'.
How can you find the annual interest rate if you know the final amount owed and the initial principal after a certain period?
-You can use the formula e^(10r) = final amount / initial principal, then take the natural logarithm (LN) of both sides to solve for r.
What is the natural logarithm function in Excel?
-The natural logarithm function in Excel is 'LN'. It is used to calculate the power to which e must be raised to obtain a given number.
If you borrowed $50 and it continuously compounded to $500 over 10 years, what was the annual interest rate?
-Using the formula e^(10r) = 10, you would find that r = LN(10) / 10, which equals approximately 0.23 or 23%.
Why is continuous compounding interest powerful over time?
-Continuous compounding interest is powerful because it compounds at an infinite number of intervals within a year, leading to exponential growth and potentially large amounts owed over time.
What is the practical implication of understanding continuous compounding interest?
-Understanding continuous compounding interest is important for financial planning, investment strategies, and making informed decisions about loans and savings.
How does the script encourage viewers to reinforce their understanding of continuous compounding interest?
-The script encourages viewers to rewatch previous videos, play with numbers, and take the limit as n approaches infinity to prove the existence of e, which will help them gain an intuitive understanding and remember the formula Pe^(rt).
Outlines
📚 Continuous Compound Interest Basics
This paragraph introduces the concept of continuous compound interest. It explains that if you borrow a principal amount \( P \) dollars for one year at an interest rate \( r \), compounded continuously, you would owe \( P \times e^r \) at the end of the year. The explanation extends to borrowing for multiple years, showing that after two years, the amount owed would be \( P \times e^{2r} \), and in general, for \( t \) years, it would be \( P \times e^{rt} \). The paragraph also provides an example with \( P = $1,000 \), \( r = 25\% \), and \( t = 3 \) years, calculating the owed amount to be approximately $2,117 using Excel's exp function to demonstrate the power of continuous compounding.
🔍 Calculating the Unknown Continuous Compound Interest Rate
The second paragraph delves into how to determine the interest rate \( r \) when the final amount owed after continuous compounding is known. Using the formula \( P \times e^{rt} \) and given that \( P = $50 \), \( t = 10 \) years, and the final amount is $500, the paragraph guides through the steps of dividing both sides of the equation by the principal \( P \) to isolate \( e^{10r} \) and setting it equal to the final amount divided by the principal, which simplifies to \( e^{10r} = 10 \). The solution involves taking the natural logarithm of both sides to solve for \( 10r \), using Excel's LN function to find that \( \ln(10) \approx 2.3 \), and then dividing by 10 to find the annual interest rate \( r \approx 0.23 \) or 23%. This demonstrates the exponential growth of debt when interest is compounded continuously at a significant rate over a long period.
Mindmap
Keywords
💡Principal
💡Interest Rate
💡Continuous Compounding
💡e (Euler's number)
💡Compounding Interval
💡Formula
💡Excel
💡Logarithm
💡Natural Log
💡Power
💡Limit
Highlights
Borrowing P dollars with a continuous compounding interest rate of r results in owing P times e to the r dollars after one year.
After two years, the amount owed is Pe to the 2r, where the initial amount owed after one year becomes the new principal.
In general, for borrowing P dollars at a rate of r for t years, the formula Pe to the rt is used to calculate the owed amount.
An example is given where borrowing $1,000 at a 25% interest rate compounded continuously for three years results in owing $2,117.
The power of compounding interest is demonstrated, showing how it can quickly lead to large sums.
Another example involves borrowing $50 at an unknown rate r compounded continuously for 10 years to owe $500, leading to solving for r.
The formula e to the 10r equals 10 is used to find the unknown interest rate.
Using logarithms, specifically the natural log, to solve for the interest rate r in the context of continuous compounding.
Excel functions such as exp for e to the power and LN for the natural log are mentioned for calculations.
The natural log of 10 is calculated to be approximately 2.3, which helps in determining the interest rate.
The interest rate r is found to be 0.23 or 23%, meaning a 10x return on the initial amount after 10 years of continuous compounding.
The importance of understanding the concept of continuous compounding and its impact on the growth of invested money is emphasized.
The video encourages viewers to review logarithm videos for a better grasp of the calculations involved.
The concept of e and its prevalence in various mathematical applications is briefly discussed.
The video concludes with advice to practice with numbers and understand the limit concept related to continuous compounding.
A challenge is presented to viewers to prove the limit as n approaches infinity of (1 + 1/n)^n converging to e.
The video aims to help viewers develop a lasting understanding and memory of the continuous compounding formula Pe to the rt.
Transcripts
Browse More Related Video

Interest (part 2) | Interest and debt | Finance & Capital Markets | Khan Academy

Interest Compounded Continuously
Compound Interest & Population Growth Word Problems - Logarithms

Introduction to interest | Interest and debt | Finance & Capital Markets | Khan Academy

Compound Interest

Introduction to compound interest and e | Algebra II | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: