Math 1325 Lecture 9 2 - Continuous Functions & Limits at Infinity

Michael Bailey
9 May 201614:42
EducationalLearning
32 Likes 10 Comments

TLDRThis lecture on section 9.2 delves into the concept of limits at infinity and the continuity of functions. A function is considered continuous if its graph is smooth, without gaps or jumps. Continuity at a point C is determined by three criteria: the existence of f(C), the existence of the limit as X approaches C, and the limit matching the value of f(C). The domain of a function is pivotal in identifying discontinuities, such as zeros in the denominator of a fraction. The lecture also covers interval and set notation for representing ranges of X values and provides methods to evaluate limits at infinity using basic rules for rational functions. Examples are given to illustrate the process of finding limits and identifying asymptotes, both horizontal and vertical, which are lines that a function approaches but never reaches. The importance of understanding these mathematical concepts is emphasized for a deeper comprehension of calculus.

Takeaways
  • 📈 A function is considered continuous if its graph is smooth without holes or jumps.
  • 🔍 To prove continuity at a point C, a function must satisfy three conditions: existence of f(C), existence of the limit as X approaches C, and the limit equals f(C).
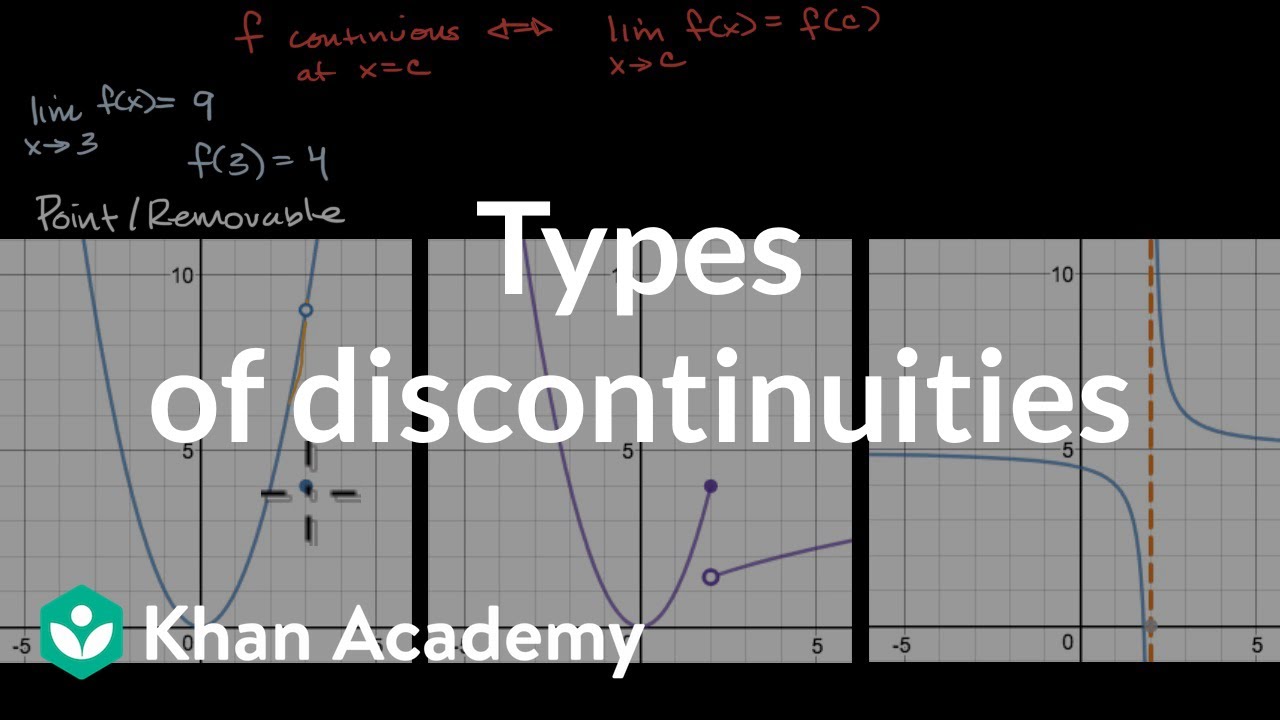
  • ⛔ If any of the three continuity conditions are not met, the function is discontinuous at that point.
  • 🚫 For rational expressions, zeros are not allowed in the denominator, and negative numbers under square roots are not permitted.
  • 📌 To find where a function is discontinuous, set the denominator equal to zero and solve for X.
  • 📊 Interval notation uses brackets to include values and parentheses to exclude them, representing ranges along the X-axis.
  • 🔢 Set notation defines a range with a squiggly bracket, a straight vertical line, and an equation or description.
  • 📐 Polynomials are continuous for all values, while rational functions are continuous except where the denominator equals zero.
  • 🔁 Piecewise functions require checking for continuity at the break points in the intervals.
  • 🧮 To evaluate limits at infinity, apply basic rules such as dividing by the largest power of X for rational equations.
  • 🏁 A horizontal asymptote is a line y=B that the function approaches as X goes to positive or negative infinity.
  • 🔍 A vertical asymptote occurs where the function's Y values approach positive or negative infinity at a specific value of X.
Q & A

  • What is the definition of a continuous function?

    -A function is continuous if it has a smooth graph without any holes, gaps, or jumps. You can draw the entire graph without lifting your pencil from the graph paper.

  • What are the three criteria a function must meet to be considered continuous at a point C?

    -For a function to be continuous at a point C, it must: 1) have a value for f(C), 2) have an existing limit as X approaches C, and 3) have the limit as X approaches C equal to the Y value or f(C).

  • What is the significance of the domain of a function in determining continuity?

    -The domain of a function indicates the values of X that are allowed. Discontinuities can occur where the function is not defined, such as zeros in the denominator of a fraction or negative numbers inside the square root.

  • How do you find the values of X where a function is discontinuous due to a hole in the graph?

    -To find where a function is discontinuous due to a hole, set the denominator of the function equal to zero and solve for X.

  • What are the two types of notations used to write intervals or ranges along the x-axis?

    -The two types of notations are interval notation, which uses square brackets and parentheses to indicate included and excluded values, and set notation, which uses a squiggly bracket and a straight vertical line followed by an equation or description.

  • How can you determine if a rational function is continuous?

    -A rational function is continuous at all values except those that make the denominator equal to zero. You can set the denominator equal to zero to find these discontinuities.

  • What are the basic rules for evaluating limits at infinity for rational equations?

    -The basic rules are: 1) If there are only numbers in the numerator and X to any power in the denominator, the limit will equal 0. 2) If there is just X or X raised to a power in the denominator, the limit does not exist as it grows to positive or negative infinity.

  • How do you find the limit of a rational function as X approaches infinity?

    -To find the limit at infinity, divide each term in the numerator and each term in the denominator by the largest power of X, then simplify to find the limit.

  • What is a horizontal asymptote and how is it determined?

    -A horizontal asymptote is a line y equals a constant or f(X) equals a constant, which is the same value as the limit at infinity for the function. If the limit as X approaches positive or negative infinity of f(X) equals B, then the line y equals B is the horizontal asymptote of f(X).

  • What is a vertical asymptote and how can you identify it?

    -A vertical asymptote is a line x equals a specific value where the function's Y values approach positive or negative infinity. It can be identified by observing the graph where the function curves up and down to both infinities at a specific X value.

  • What is the role of factoring in evaluating the continuity of a rational function?

    -Factoring helps to identify the values of X that make the denominator zero, which are points of discontinuity. Even though the original function might be simplified, when considering continuity, the original equation must be used to find these points.

  • How can you determine if a piecewise function is continuous at the break point?

    -To determine continuity at the break point, plug the break value into each piece of the piecewise function and solve. If the one-sided limits from both sides of the break point are not the same, the function is not continuous at that point.

Outlines
00:00
📈 Understanding Continuity and Limits

This paragraph introduces the concept of continuity in functions, explaining that a function is continuous if its graph is smooth without any gaps or jumps. It outlines three criteria for continuity at a point C: existence of the point f(C), the limit as X approaches C must exist, and the limit as X approaches C must equal the function's value at C. The paragraph also discusses how to determine the domain of a function and identify points of discontinuity, such as when the denominator of a fraction is zero. It concludes with an explanation of interval and set notation used to express the domain and ranges of functions.

05:02
🔍 Evaluating Continuity and Limits at Infinity

The second paragraph delves into how to assess the continuity of more complex functions, such as rational expressions, and how factoring can simplify the process. It emphasizes the importance of considering the original equation when checking for continuity, not a simplified version. The paragraph explains how to find values that cause discontinuity by setting factors equal to zero and solving. It also covers different types of functions (rational, polynomial, and piecewise) and their continuity characteristics. Additionally, it teaches how to evaluate limits as X approaches infinity using basic rules and how to apply these rules to rational equations by dividing each term by the largest power of X.

10:03
📊 Limits at Infinity and Asymptotes

The final paragraph focuses on calculating limits as X approaches positive or negative infinity for rational equations. It illustrates how to simplify expressions by dividing each term by the highest power of X present. The paragraph provides examples to show how this process leads to determining the limit's value or concluding that it does not exist. It also introduces the concept of asymptotes, explaining both horizontal and vertical asymptotes. A horizontal asymptote is a constant value that the limit approaches as X goes to infinity, while a vertical asymptote occurs where the function's output tends toward infinity at a specific X value. The paragraph concludes with an example graph demonstrating these concepts.

Mindmap
Keywords
💡Continuity
Continuity in a mathematical function refers to the property where the function has a smooth graph without any holes, gaps, or jumps. In the context of the video, a function is considered continuous at a point if it meets three criteria: the function value at that point exists, the limit as X approaches that point exists, and the limit is equal to the function value at that point. Continuity is a fundamental concept in calculus and is essential for understanding limits and the behavior of functions.
💡Limit
A limit in calculus is a value that a function or sequence approaches as the input (or index) approaches some value. The video discusses limits in the context of both a specific point (where X approaches a constant value C) and infinity (where X approaches positive or negative infinity). Limits are crucial for defining the behavior of functions, especially at points where the function may not be explicitly defined, such as at discontinuities or as the function grows without bound.
💡Domain
The domain of a function is the set of all possible input values (often X-values) for which the function is defined. The video emphasizes the importance of understanding the domain when discussing continuity, as the domain will exclude values that cause issues like division by zero or taking the square root of a negative number. For instance, the video mentions that for fractions, the denominator cannot be zero, which defines the domain of the function.
💡Interval Notation
Interval notation is a mathematical notation used to describe a subset of the real numbers. It is depicted in the video as a way to represent the set of all X-values for which a function is continuous. The notation uses brackets and parentheses to indicate whether the endpoints of the interval are included or excluded. For example, the video uses interval notation to express that a function is discontinuous at a specific point, excluding that point from the set of continuous values.
💡Set Notation
Set notation is a way to describe a collection of mathematical objects, such as numbers or functions. In the video, set notation is used to define the domain of a function or the set of points where a function is continuous. It is particularly useful for expressing conditions and rules about the values that a variable can or cannot take. The video demonstrates using set notation to describe the values of X for which the function is undefined, indicating discontinuity.
💡Rational Expression
A rational expression is a mathematical expression that can be written as the quotient of two polynomials. The video discusses rational expressions in the context of continuity, noting that such expressions are continuous everywhere except where the denominator is zero, which would create a discontinuity. Rational expressions are a common source of discontinuities in functions and are an important topic in calculus.
💡Polynomial
A polynomial is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, and multiplication, and non-negative integer exponents of variables. The video mentions that polynomials are continuous for all values of X, making them an example of functions with no discontinuities. This is significant because it contrasts with other types of functions, like rational expressions, which can have discontinuities.
💡Piecewise Function
A piecewise function is a function that is defined by multiple sub-functions, each applicable to a different interval of the function's domain. The video discusses how to evaluate the continuity of piecewise functions by checking the function's behavior at the points where the sub-functions change, known as breaks. The continuity of a piecewise function is determined by ensuring the function meets the criteria for continuity across these transition points.
💡Asymptote
An asymptote is a line that a function approaches but never actually reaches. The video distinguishes between two types of asymptotes: horizontal and vertical. A horizontal asymptote is a constant value that the limit of a function approaches as X goes to positive or negative infinity. The video provides an example where y equals 2 is a horizontal asymptote. A vertical asymptote occurs when the function's value grows without bound as X approaches a specific value. The video illustrates this with an example where X equals 3 is a vertical asymptote.
💡One-Sided Limits
One-sided limits are limits approached from either the left side or the right side of a point. The video explains that to determine continuity at a point, one must check both the left-sided and right-sided limits as X approaches that point. If these one-sided limits are not equal, the function is not continuous at that point. This concept is important for understanding how functions behave at discontinuities, such as jumps or breaks in the function.
💡Factoring
Factoring is the process of breaking down a polynomial or rational expression into its constituent factors. In the context of the video, factoring is suggested as a method to simplify the process of finding discontinuities in rational expressions by setting each factor equal to zero. This technique helps identify the values of X that cause the function to be undefined, thereby indicating points of discontinuity.
Highlights

A function is considered continuous if it has a smooth graph without any holes, gaps, or jumps.

Three criteria must be met for a function to be continuous at a point C: existence of f(C), existence of the limit as X approaches C, and the limit being equal to the value of f(C).

The domain of a function and values outside the domain can help determine continuity, especially for fractions where zeros are not allowed in the denominator.

Interval notation and set notation are two ways to represent ranges along the x-axis, with different symbols to indicate included or excluded values.

Rational functions are continuous everywhere except where the denominator equals zero, while polynomials are continuous for all values.

Piecewise functions require checking at the break in intervals to evaluate continuity.

To find the limit as X approaches a specific value, plug that value into the function and compare the left and right-sided limits.

Basic rules for evaluating limits at infinity include recognizing when a limit equals zero or does not exist due to the function's unbounded growth.

For rational equations, divide each term by the largest power of X to evaluate limits at infinity analytically.

A horizontal asymptote is a line y=B where B is the limit of the function as X approaches positive or negative infinity.

A vertical asymptote occurs where the function's values approach positive or negative infinity at a specific value of X.

The existence of asymptotes can be determined by examining the behavior of the function as X approaches certain values.

The concept of limits is crucial in calculus for understanding the behavior of functions at particular points or as they approach infinity.

Continuity is a fundamental property of functions that affects their graphical representation and mathematical analysis.

The use of interval and set notation is essential for clearly defining the domain and range of functions.

Factoring can simplify the process of determining where a rational function is discontinuous by setting the denominator equal to zero.

The behavior of functions at breaks in piecewise functions is critical to establish continuity across different intervals.

Homework exercises are recommended to practice evaluating continuity, limits, and identifying asymptotes.

Transcripts

Browse More Related Video

Math 133 Lecture 2 6

Business Calculus - Math 1329 - Section 1.5 (and 1.6) - Limits and Continuity

Types of discontinuities | Limits and continuity | AP Calculus AB | Khan Academy

Continuity!

1.2 - Algebraic Limits and Continuity

AP Calculus AB - 1.15 Connecting Limits at Infinity and Horizontal Asymptotes

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsLimitsContinuityInfinityFunction AnalysisRational FunctionsPolynomialsPiecewise FunctionsInterval NotationSet NotationAsymptotes