Math 133 Lecture 2 6
TLDRThis lecture delves into the concept of limits at infinity for functions, focusing on how a function behaves as the input variable X grows without bound. The discussion begins with rational functions and the comparison of limits as X approaches positive or negative infinity. The lecturer introduces horizontal asymptotes, which are horizontal lines that a function approaches as X tends to infinity. Several examples are provided to illustrate how to calculate these limits, including the use of common factorization and the application of limit theorems. The lecture also distinguishes between horizontal and vertical asymptotes, noting that the latter occurs when the limit at a certain point results in positive or negative infinity. The script concludes with the exploration of limits for trigonometric functions and polynomials, emphasizing the importance of understanding these mathematical concepts for analyzing the behavior of functions at extreme values.
Takeaways
- 📚 The lecture focuses on understanding the behavior of functions as the variable X approaches infinity or negative infinity, which is crucial for determining horizontal asymptotes.
- 🔍 When X approaches infinity, the limit of a rational function can be evaluated by comparing the highest degree terms in the numerator and denominator.
- 📈 The limit of a function as X approaches infinity can be used to predict the end behavior of the function and identify horizontal asymptotes, which are constant values that the function approaches but never actually reaches.
- 📉 For rational functions, the horizontal asymptote can be determined by looking at the ratio of the leading coefficients of the numerator and the denominator when X is very large.
- 🤔 The concept of indeterminate forms arises when expressions like 0/0, ∞/∞, 0×∞, ∞ - ∞, or quantities with differing signs approaching infinity are encountered, necessitating further manipulation to resolve.
- 🧮 The limit of a function as X approaches a certain value can be found using various limit rules and theorems, such as the rule for polynomial powers and the squeeze theorem.
- 🚫 Not all functions have a limit as X approaches infinity; functions like sine and cosine are periodic and do not approach a single value as X increases without bound.
- ➗ To find vertical asymptotes, set the denominator of the function equal to zero and solve for X. Then, evaluate the limit as X approaches these values to determine if they result in positive or negative infinity.
- 📊 The graph of a function can provide visual insights into its behavior, such as identifying horizontal and vertical asymptotes, and can be analyzed using tools like Desmos.
- ✅ It is essential to verify both positive and negative infinity limits when determining horizontal asymptotes, as they may differ, leading to multiple horizontal asymptotes for a single function.
- ⛔ The absence of a limit for a function as X approaches infinity indicates that the function does not settle to a specific value or infinity in either direction, as seen with oscillating functions like sine and cosine.
Q & A
What is the main objective of Lecture 2.6?
-The main objective of Lecture 2.6 is to investigate the behavior of a given function as the variable X becomes very large, either approaching positive or negative infinity.
What is a horizontal asymptote?
-A horizontal asymptote is a horizontal line that a function approaches as X approaches positive or negative infinity. It represents the limit of a function at infinity.
How does the behavior of a rational function as X approaches infinity differ from when X approaches a finite value?
-When X approaches a finite value, the limit is the value the function approaches as it gets closer to that finite number. However, when X approaches infinity, the limit is the value the function approaches without bound, which could be a number, infinity, or negative infinity.
What does it mean when the limit of a function as X approaches infinity is equal to 1?
-When the limit of a function as X approaches infinity is equal to 1, it means that as X becomes larger and larger, the function values get closer and closer to 1. This suggests a horizontal asymptote at y = 1.
What is the general definition of the limit of a function as X approaches infinity?
-The limit of a function as X approaches infinity is defined as the value L that the function f(X) approaches as X becomes larger and larger, without bound.
What is the limit of 1/X as X approaches infinity?
-The limit of 1/X as X approaches infinity is equal to zero. This is because as X becomes very large, the value of 1 divided by X becomes very small, approaching zero.
What are the possible behaviors of a function as X approaches infinity?
-As X approaches infinity, a function can approach a constant value (horizontal asymptote), oscillate around a value with decreasing amplitude, or the function could diverge to positive or negative infinity.
What is an indeterminate form and how is it resolved?
-An indeterminate form occurs when an expression results in 0/0, ∞/∞, 0·∞, ∞ - ∞, or similar cases that do not directly provide a numerical value. It is resolved by algebraic manipulation, such as factoring or simplifying the expression, to determine the actual limit.
How do you determine if a value is a vertical asymptote of a function?
-A value is a vertical asymptote of a function if the function's limit as X approaches that value is either positive or negative infinity. It is often identified by setting the denominator of the function equal to zero and solving for X.
What is the limit of the sine function as X approaches infinity?
-The limit of the sine function does not exist as X approaches infinity because the sine function oscillates between -1 and 1, and there is no single value to which it approaches.
What happens to the limit of a function when you multiply the numerator and denominator by the conjugate of the denominator?
-Multiplying the numerator and denominator by the conjugate of the denominator helps to eliminate the radical or complex parts in the denominator, simplifying the expression and allowing you to find the limit, especially when dealing with indeterminate forms like 0/0.
Outlines
📚 Introduction to Limits at Infinity and Horizontal Asymptotes
This paragraph introduces the concept of limits at infinity and horizontal asymptotes. It discusses the behavior of functions as the variable X approaches infinity or negative infinity. A rational function is used as an example to illustrate how to evaluate these limits. The paragraph also explains the difference between limits at a finite number and limits at infinity, and introduces the general definition of a limit at infinity.
📈 Horizontal Asymptotes and Their Calculations
The second paragraph delves into horizontal asymptotes, explaining how to graph them using Desmos and how to determine them by looking at the behavior of functions as X approaches infinity or negative infinity. It highlights that horizontal asymptotes can differ for positive and negative infinity and emphasizes the need to be cautious of this when evaluating limits. The paragraph also presents a theorem for rational functions involving positive exponents and their behavior at infinity.
🔢 Simplifying Rational Functions to Find Limits
This paragraph focuses on the process of simplifying rational functions to find their limits as X approaches infinity. It explains how to factor out the highest degree terms and how to deal with indeterminate forms such as 0/0 or ∞/∞. The paragraph also demonstrates how to simplify expressions involving square roots and absolute values, leading to the determination of horizontal asymptotes.
🔍 Identifying and Simplifying Functions for Limits at Infinity
The fourth paragraph continues the discussion on limits at infinity, showing how to factor and simplify functions to remove indetermination and find the correct limits. It covers the use of common factors and the importance of considering the sign of X when dealing with absolute values. The paragraph concludes with the identification of horizontal asymptotes based on the simplified form of the function.
🚫 Understanding Vertical Asymptotes and Their Calculation
The fifth paragraph shifts the focus to vertical asymptotes, contrasting them with horizontal asymptotes. It explains that vertical asymptotes occur when the limit of a function as X approaches a certain value results in positive or negative infinity. The paragraph outlines the process of finding vertical asymptotes by setting the denominator equal to zero and verifying the limit at those points.
🧮 Computing Limits for Rational Functions with Factoring
In this paragraph, the process of computing limits for rational functions is further explored with an emphasis on factoring. It demonstrates how to deal with different cases when X approaches specific values, such as zero, and how to determine if these points are vertical asymptotes. The paragraph also shows how to simplify expressions and use factoring to find the limits at these points.
📉 Limits of Trigonometric Functions at Infinity
The sixth paragraph discusses the behavior of trigonometric functions, such as sine and cosine, as X approaches infinity. It explains that these functions do not have a limit at infinity due to their oscillatory nature. The paragraph also covers the limit of arctan(X) as X approaches specific values, highlighting the use of the arctan function's graph to determine limits.
🔁 Limits at Infinity for Power Functions
The seventh paragraph examines the limits at infinity for power functions, such as X cubed and X squared. It shows how the sign of infinity (positive or negative) affects the limit and how to determine the limit by considering the highest power term in the function. The paragraph also includes examples of how to simplify expressions and use factoring to find these limits.
✅ Conclusion and Summary of Limit Concepts
The final paragraph concludes the lecture by summarizing the concepts of limits at infinity. It touches on the different types of limits, including limits that result in a number, infinity, or undefined due to oscillation. The paragraph provides examples of how to handle indeterminate forms by using conjugates and emphasizes the importance of understanding the behavior of functions as X approaches infinity or negative infinity.
Mindmap
Keywords
💡Limit at Infinity
💡Horizontal Asymptote
💡Rational Function
💡Indeterminate Form
💡Polynomial
💡Absolute Value
💡Factoring
💡Theorem
💡Conjugate
💡Sine and Cosine
💡Arctangent
Highlights
The lecture investigates the behavior of functions as x approaches infinity or negative infinity.
Evaluates the limit of rational functions as x becomes large.
Conjectures that the limit of x^2/(x^2+1) as x approaches infinity is equal to 1.
Discusses the concept of horizontal asymptotes and their calculation.
Differentiates between limits as x approaches a number vs infinity or negative infinity.
Introduces the general definition of limits at infinity and their intuitive understanding.
Explains how to identify and calculate horizontal asymptotes using limits.
Demonstrates the use of a theorem for rational functions with positive powers of x.
Provides an example to show how to compute limits and identify horizontal asymptotes.
Discusses the possibility of different horizontal asymptotes for positive and negative infinity.
Explains how to handle square roots and absolute values when evaluating limits.
Computes limits and identifies horizontal asymptotes for various functions.
Introduces the concept of vertical asymptotes and their calculation.
Differentiates between horizontal and vertical asymptotes in terms of limit behavior.
Provides examples to illustrate the calculation of vertical asymptotes.
Discusses the limit behavior of trigonometric and logarithmic functions at infinity.
Shows how to handle indeterminate forms when evaluating limits at infinity.
Summarizes the key concepts and methods for analyzing limits at infinity in functions.
Transcripts
Browse More Related Video

Business Calculus - Math 1329 - Section 1.5 (and 1.6) - Limits and Continuity

AP Calculus AB - 1.15 Connecting Limits at Infinity and Horizontal Asymptotes

Math 1325 Lecture 9 2 - Continuous Functions & Limits at Infinity
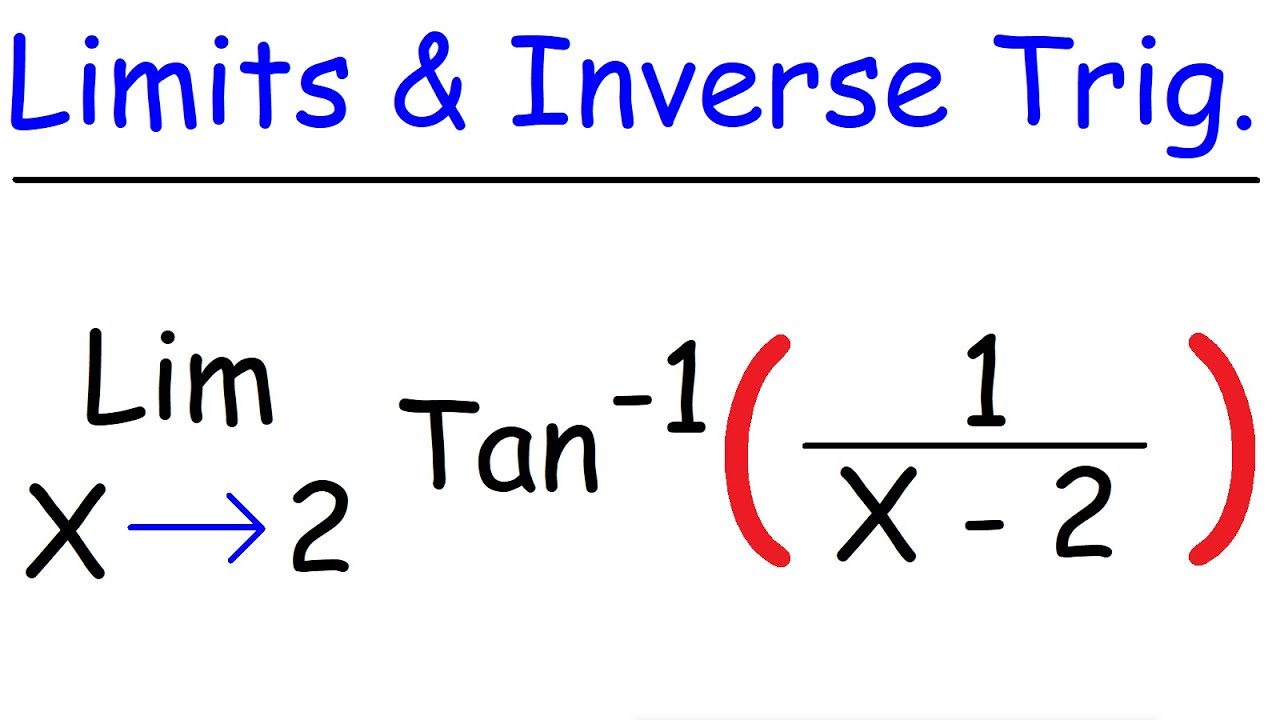
Limits of Inverse Trigonometric Functions | Calculus

Calculus:Limits of Rational Functions

Limits at infinity of quotients (Part 2) | Limits and continuity | AP Calculus AB | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: