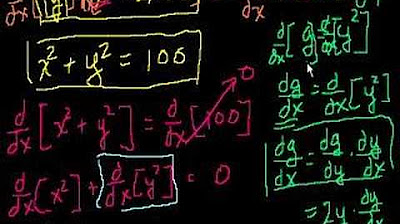Implicit Differentiation for Calculus - More Examples, #1
TLDRThe video script focuses on the process of implicit differentiation, which is a technique used to find the derivative of equations where variables are not isolated on one side of the equation. The speaker begins by illustrating the differentiation of a simple equation, \(x^2 + y^2 = 25\), and explains the steps to isolate \(\frac{dy}{dx}\). They then tackle a more complex equation involving trigonometric functions, \(\cos^2(x) + \sin^3(y) = 0.6\), and demonstrate the use of the chain rule to differentiate both sides with respect to \(x\). The speaker emphasizes the importance of multiplying by \(\frac{dy}{dx}\) when differentiating terms involving \(y\). The final expressions for \(\frac{dy}{dx}\) are simplified and presented clearly. The script serves as an educational guide for those looking to understand implicit differentiation in calculus.
Takeaways
- 📚 Implicit differentiation involves differentiating both sides of an equation with respect to x, even when y is involved.
- 🔑 When differentiating y to the power of any number, remember to multiply by dy/dx.
- ⚖️ For the equation x^2 + y^2 = 25, the derivative dy/dx is found by isolating dy/dx and simplifying to -x/y.
- 🌀 In the case of cosine(x)^2 + sine(y^3) = 0.6, the chain rule is applied to differentiate both x and y terms.
- 🔄 The derivative of cosine(x)^2 is -2x * sine(x), and for sine(y^3) it's 3y^2 * cosine(y) * dy/dx.
- ➗ To solve for dy/dx, isolate it by moving non-dy/dx terms to one side of the equation and dividing through by the y term.
- 🔢 The final derivative for the second example is dy/dx = (2x * sine(x)^2) / (3y^2 * cosine(y)^3).
- ⛓ The chain rule is crucial when differentiating composite functions, such as sine or cosine of a variable.
- 🧩 Each term in the derivative equation must be treated separately and then brought together to solve for dy/dx.
- ✅ Practice is key to mastering implicit differentiation, as it requires a good understanding of derivative rules and the chain rule.
- 📉 The derivative of a constant is zero, which simplifies the differentiation process for constants within the equation.
Q & A
What is the main characteristic of an implicit equation that distinguishes it from an explicit one?
-An implicit equation has variables, such as x and y, on the same side of the equal sign, as opposed to explicit equations where the variable is isolated on one side.
When differentiating an implicit equation, why do we need to use dy/dx when taking the derivative of a term involving y?
-We use dy/dx to account for the rate of change of y with respect to x, which is necessary when differentiating terms that include y in implicit differentiation.
What is the derivative of x squared with respect to x?
-The derivative of x squared (x^2) with respect to x is 2x.
How do you simplify the expression for dy/dx in the equation x squared plus y squared equals 25 after implicit differentiation?
-After subtracting 2x from both sides and dividing by 2y, the expression simplifies to dy/dx = -x/y.
In the context of the script, what is the chain rule?
-The chain rule is a method used in calculus for finding the derivative of a composite function. It states that the derivative of the composite function is the derivative of the outer function times the derivative of the inner function.
What is the derivative of cosine of x squared with respect to x?
-The derivative of cosine of x squared with respect to x, using the chain rule, is -2x * sine of x.
What is the derivative of sine of y cubed with respect to y?
-The derivative of sine of y cubed with respect to y, using the chain rule, is 3y squared * cosine of y.
How do you isolate dy/dx in the equation cosine of x squared plus sine of y cubed equals 0.6 after implicit differentiation?
-You isolate dy/dx by moving all other terms to one side of the equation and then dividing both sides by the term that includes y, which is 3y squared * cosine of y cubed.
What is the final simplified form of dy/dx for the equation cosine of x squared plus sine of y cubed equals 0.6 after implicit differentiation?
-The final simplified form of dy/dx is 2x * sine of x squared, all over 3y squared * cosine of y cubed.
Why is it important to isolate dy/dx when performing implicit differentiation?
-Isolating dy/dx is important because it provides the derivative of y with respect to x, which is the main goal of differentiating an implicit equation.
What is the role of the constant term (0.6 in the example) in the differentiation process of an implicit equation?
-The constant term does not change when taking the derivative with respect to x, so its derivative is zero, simplifying the process of solving for dy/dx.
How does the process of implicit differentiation help in finding the slope of the tangent line to a curve at any point (x, y)?
-Implicit differentiation allows us to find the derivative dy/dx, which represents the slope of the tangent line to the curve at any point (x, y), even when y is not isolated.
Outlines
📚 Implicit Differentiation Basics
This paragraph introduces the concept of implicit differentiation, where both x and y are on the same side of the equation. The example given is x^2 + y^2 = 25, and the process involves taking the derivative of both sides with respect to x. The derivative of x^2 is 2x, and for y^2, it's 2y times dy/dx. The right side derivative results in 0. The solution is obtained by isolating dy/dx and simplifying to get dy/dx = -x/y.
🔍 Advanced Implicit Differentiation with Trigonometric Functions
The second paragraph delves into a more complex example involving the derivative of cos(x^2) + sin(y^3) = 0.6. This requires the use of the chain rule. The derivative of cos(x^2) is -sin(x^2) * 2x, and for sin(y^3), it's cos(y^3) * 3y^2 times dy/dx. The constant 0.6 has a derivative of 0. The goal is to solve for dy/dx, which is achieved by moving terms around and dividing by 3y^2 * cos(y^3), resulting in dy/dx = (2x * sin(x^2)) / (3y^2 * cos(y^3)).
Mindmap
Keywords
💡Implicit Differentiation
💡Derivative
💡Chain Rule
💡dy/dx
💡Cosine Function
💡Sine Function
💡Square
💡Cube
💡Simplifying
💡Equation
💡Trigonometric Functions
Highlights
The process of implicit differentiation involves differentiating both sides of an equation with respect to x, even when x and y are on the same side of the equation.
When differentiating y squared, the result is 2y multiplied by dy/dx, a key step in implicit differentiation.
The derivative of x squared is straightforward, resulting in 2x.
After differentiating, the goal is to isolate dy/dx on one side of the equation.
An example equation x squared plus y squared equals 25 is used to illustrate the process.
Subtracting 2x from both sides of the equation simplifies the process of solving for dy/dx.
Dividing both sides by 2y yields the derivative dy/dx = -x/y.
The transcript provides a second, more complex example involving the derivative of cosine of x squared plus sine of y cubed equals 0.6.
The chain rule is applied when differentiating cosine of x squared, resulting in -sine times 2x.
Differentiating sine of y cubed involves recognizing the derivative of y cubed as 3y squared times dy/dx.
The derivative of a constant, such as 0.6, is zero, simplifying the equation.
Rearranging terms to isolate dy/dx involves moving terms to the right side of the equation.
The final derivative for the second example is dy/dx = (2x * sine(x squared)) / (3y squared * cosine(y cubed)).
The process emphasizes the importance of correctly applying the chain rule and understanding the role of dy/dx in implicit differentiation.
Each step in the differentiation process is clearly explained, making the method accessible to learners.
The transcript serves as a tutorial for those unfamiliar with the concept of implicit differentiation.
The examples provided demonstrate the application of implicit differentiation in solving more complex equations.
The final derivatives are simplified to their most understandable form for clarity.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: