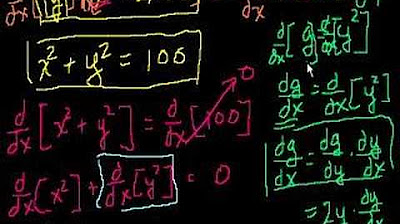Implicit Differentiation
TLDRThis lesson delves into the concept of implicit differentiation, a technique used to differentiate functions that are not explicitly defined in terms of one variable. The instructor begins by contrasting explicit functions, where one variable is defined in terms of another, with implicit functions, where both variables are intertwined within the equation. The process of implicit differentiation relies heavily on the chain rule and involves differentiating both sides of the given equation with respect to x, ensuring that any term involving y is multiplied by dy/dx. The instructor demonstrates how to isolate dy/dx to find the derivative of y with respect to x, which can be used to determine the slope of a tangent line at a specific point on the curve represented by the implicit function. The lesson includes several examples that illustrate the differentiation process and how to solve for dy/dx, emphasizing the importance of correctly applying the chain rule and factoring out common terms. The summary concludes with an example of finding the equation of a tangent line at a given point, showcasing the practical application of implicit differentiation.
Takeaways
- 📚 Implicit differentiation is used for functions where variables are not explicitly defined in terms of one another, and it requires the use of the chain rule.
- 🔑 The power rule is essential in implicit differentiation, and it involves multiplying by the derivative of the variable raised to a power.
- 🔄 When differentiating with respect to X, if a term contains a Y, it must be multiplied by dy/dx, which represents the derivative of Y with respect to X.
- 📈 An explicit function has one variable defined in terms of the other, whereas an implicit function has both variables mixed together on one or both sides of the equation.
- 🌐 The process of implicit differentiation involves applying the same rules as explicit differentiation but includes the additional step of multiplying by dy/dx for terms involving Y.
- 📉 The derivative of an explicit function is also explicit, while the derivative of an implicit function is implicit and contains both X and Y variables.
- ✅ To verify different forms of a derivative, plug in a point of tangency into each form and ensure the slopes match.
- 🧩 When solving for dy/dx, terms with dy/dx are collected on one side of the equation, and terms without are isolated on the other side.
- 🔢 The derivative dy/dx can be found by factoring out dy/dx from the terms on one side of the equation and then dividing to solve for dy/dx.
- 📝 When evaluating the derivative at a specific point, substitute the x and y values from that point into the derivative to find the slope of the tangent line at that point.
- 📐 The equation of the tangent line at a specific point can be written using the point-slope form of a line, with the slope found from the derivative.
Q & A
What is the main topic of the lesson?
-The main topic of the lesson is implicit differentiation, which is a method used to differentiate functions that are not explicitly defined in terms of one variable.
What is the difference between explicit and implicit functions?
-Explicit functions are those where one variable is defined in terms of the other (e.g., y = f(x)), whereas implicit functions have both variables intermixed such that neither is explicitly defined in terms of the other (e.g., x^2 + y^2 = 1).
Why is implicit differentiation necessary?
-Implicit differentiation is necessary when it is not possible to express one variable explicitly in terms of the other, and we still need to find the derivative of the relationship between the variables.
What mathematical rule is primarily used in implicit differentiation?
-The chain rule is primarily used in implicit differentiation, as it allows us to differentiate composite functions and terms involving variables that are not isolated.
How does the process of differentiating an implicit function differ from differentiating an explicit function?
-When differentiating an implicit function, we do not rearrange the function to isolate variables. Instead, we apply differentiation rules directly to the given equation, and we multiply terms containing y by dy/dx, as required by the chain rule. The resulting derivative will include both x and y variables.
What is the general approach to solving for dy/dx after differentiating both sides of an implicit function with respect to x?
-After differentiating both sides, terms containing dy/dx are collected on one side of the equation, and terms without dy/dx are moved to the other side. Then, factor out dy/dx from the terms on one side and solve for dy/dx by dividing both sides by the remaining expression.
What is the significance of finding the slope of the tangent line at a particular point on a curve?
-The slope of the tangent line at a particular point on a curve is the instantaneous rate of change at that point. It is represented by the derivative of the function at that point and is crucial for understanding the behavior of the function locally.
How does the appearance of the derivative of an explicit function differ from that of an implicit function?
-The derivative of an explicit function is also explicit and only contains the variable with respect to which the derivative is taken (e.g., dy/dx in terms of x). In contrast, the derivative of an implicit function is implicit and contains both variables (e.g., dy/dx in terms of both x and y).
What is the product rule used for in differentiation?
-The product rule is used when differentiating a product of two functions. It states that the derivative of the product is the derivative of the first function times the second function plus the first function times the derivative of the second function (f'g + fg').
How can you verify if different forms of the derivative are correct?
-You can verify the correctness of different forms of the derivative by plugging in a point of tangency into each form and ensuring that the calculated slopes are the same.
What is the process for writing the equation of the tangent line at a specific point on a curve?
-To write the equation of the tangent line, first find the derivative of the function to get the slope of the tangent line. Then, use the point-slope form of a line (y - y1 = m(x - x1)) where m is the slope and (x1, y1) is the point of tangency. Finally, simplify the equation to the desired form.
Outlines
📚 Introduction to Implicit Differentiation
The first paragraph introduces the concept of implicit differentiation, which is a technique used to differentiate functions that are not explicitly defined in terms of one variable. It explains the difference between explicit and implicit functions and emphasizes the need for implicit differentiation when variables are intertwined in a single equation. The paragraph also reviews basic derivative rules and the chain rule, which is fundamental for implicit differentiation.
🔗 Chain Rule and Implicit Differentiation
The second paragraph delves into the application of the chain rule during implicit differentiation. It discusses how to handle terms involving 'y' in the differentiation process and how the chain rule is used to multiply by the derivative of the inner function. The distinction between explicit and implicit derivatives is also highlighted, with an example showing how the same function can yield different forms of derivatives based on whether it's treated explicitly or implicitly.
📝 Steps for Implicit Differentiation
The third paragraph outlines the steps for differentiating an implicit function. It emphasizes not manipulating the function and applying the same differentiation rules as with explicit functions, but with the addition of multiplying by dy/dx wherever 'y' appears. The paragraph also discusses rearranging terms to isolate dy/dx and factoring it out to solve for the derivative of 'y' with respect to 'x'.
🔍 Evaluating Derivatives at a Point
The fourth paragraph focuses on evaluating the derivative at a specific point of tangency. It illustrates how to find the slope of the tangent line at a given point using both explicit and implicit derivatives. The paragraph demonstrates that despite their different appearances, both types of derivatives can lead to the same slope at a particular point, thus verifying their correctness.
🧮 Implicit Differentiation with Examples
The fifth paragraph provides an example of implicit differentiation without manipulating the original function. It shows the step-by-step process of differentiating terms involving 'x' and 'y' and rearranging the equation to solve for dy/dx. The paragraph also touches on the possibility of having different forms of the derivative and verifying correctness by checking the slope at a point of tangency.
🔑 Solving for the Derivative and Tangent Line
The sixth paragraph continues with examples of implicit differentiation, showing how to solve for the derivative and then use it to find the equation of the tangent line at a specific point. It demonstrates the process of differentiating, simplifying the derivative expression, and using a given point to find the slope of the tangent line. The paragraph concludes with verifying the work by comparing the derived tangent line equation with the original function.
📈 Final Thoughts on Implicit Differentiation
The seventh and final paragraph summarizes the process of implicit differentiation and its application to word problems in the next topic. It encourages students to practice the process as formatted in the homework, avoiding the quotient rule in favor of cross-multiplication for simpler calculations. The paragraph ends with an offer for additional help and a sign-off until the next lesson.
Mindmap
Keywords
💡Implicit Differentiation
💡Explicit Function
💡Chain Rule
💡Product Rule
💡Derivative
💡Tangent Line
💡Power Rule
💡Quotient Rule
💡Differentiation Rules
💡Variable
💡Slope
Highlights
Introduction to implicit differentiation, a technique used to differentiate functions that are not explicitly defined in terms of one variable.
Differentiating explicit functions versus implicit functions, where the latter involves variables mixed together in an equation.
Terminology clarification: A function is explicit if one variable is defined in terms of the other, whereas an implicit function has both variables interdependent.
The necessity of using the chain rule when differentiating implicitly, as it applies to expressions raised to a power that are not simply x.
Generalization of the power rule for differentiating expressions with respect to x, including expressions involving other variables like y or u.
Differentiating an explicit function results in an explicit derivative, while differentiating an implicit function results in an implicit derivative.
The process of differentiating the function x*y = 10 both explicitly and implicitly to showcase the two methods.
The equivalence of differentiating implicitly and explicitly, as both methods yield the same slope of the tangent line at any given point.
Steps for differentiating an implicit function: Differentiate both sides of the equation with respect to x, apply the same rules as for explicit functions, and solve for dy/dx.
Rearranging terms to isolate dy/dx on one side of the equation and factoring out common terms to solve for the derivative.
Differentiating the function (x - 5y) / (2x + y) by cross-multiplying to simplify the differentiation process.
Differentiating a product of functions using the product rule, as demonstrated with the function x*y^2 + 4x*y.
The process of finding the slope of the tangent line at a given point using the derivative of the function.
Writing the equation of the tangent line at a specific point using the point-slope form of a line equation.
Verification of the derived equation of the tangent line by plugging in the point of tangency and ensuring the slope matches.
Cross-multiplication as an alternative method to simplify implicit differentiation, especially useful when dealing with quotients.
Application of implicit differentiation to solve word problems in the subsequent lesson, highlighting the practical use of the technique.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: