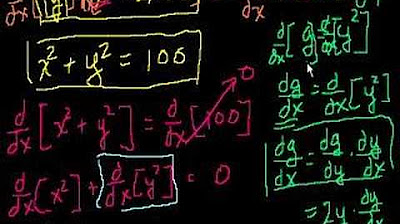Implicit Differentiation Method

Excellence Academy
12 Dec 202109:34
EducationalLearning
32 Likes 10 Comments

TLDRThe video script from Excellence Academy introduces the concept of implicit differentiation, a method used when variables x and y are not expressed separately in an equation. Unlike explicit differentiation where y is a function of x, implicit differentiation requires differentiating both x and y simultaneously. The key rule is that when differentiating y, the term dy/dx is included. The instructor uses a simple example to illustrate this method: given the equation \(2x^2y + 3y + 2x^3 = 14x\), the process involves differentiating each term with respect to x, rearranging terms, and solving for dy/dx. The final result is an expression for dy/dx in terms of x, y, and their powers, showcasing the application of implicit differentiation in solving complex mathematical problems.

Takeaways
  • 📚 Implicit differentiation is a method used when y is not expressed as a function of x and x and y are combined in the equation.
  • 🔑 The key concept in implicit differentiation is to differentiate both x and y simultaneously, with differentiation of y including the term dy/dx.
  • 📌 When differentiating x in an equation, the result remains the same as with regular differentiation.
  • 📌 When differentiating y in an equation, the result includes the term dy/dx.
  • 🌟 An example given in the script is the equation 2x^2y + 3y + x^3y^2 = 14x, which involves both x and y.
  • ✅ The differentiation process involves applying the rules of differentiation to each term, considering the presence of x and y.
  • 🔍 After differentiating, terms with dy/dx are factored on one side of the equation, and terms without are moved to the other side.
  • 🧮 The resulting equation after rearranging terms and factoring is dy/dx = (14 - 4xy - 6x^2y^2) / (2x^2 + 3 + 4x^3y).
  • 📉 To solve for y in terms of x, divide both sides of the equation by the term containing x.
  • 🔗 The final answer is expressed as y/x = (7 - 2xy - 3x^2y^2) / (2x^2 + 3 + 4x^3y), which shows the relationship between y and x.
  • ⚙️ Implicit differentiation is particularly useful for equations where y cannot be easily isolated as a function of x.
Q & A

  • What is the main concept of implicit differentiation?

    -The main concept of implicit differentiation is that both x and y are differentiated simultaneously, with differentiation of y including the term dy/dx.

  • How does implicit differentiation differ from other methods of differentiation?

    -In other methods, y is usually expressed as a function of x, whereas in implicit differentiation, x and y are combined and not expressed independently.

  • What is the rule for differentiating x in implicit differentiation?

    -When differentiating x in implicit differentiation, it remains the same, without any additional terms.

  • How is y differentiated in implicit differentiation?

    -When differentiating y in implicit differentiation, the term dy/dx is included to account for the rate of change of y with respect to x.

  • What is the given example in the script for demonstrating implicit differentiation?

    -The example given is the equation 2x^2y + 3y + 2x^3y^2 = 14x.

  • What is the result of differentiating the term 2x^2y with respect to x in the example?

    -Differentiating 2x^2y with respect to x gives 4xy (since the derivative of x^2 is 2x and we multiply by the constant 2).

  • How does the differentiation of the term 3y in the example differ from that of 3x?

    -The differentiation of 3y gives 3, similar to the differentiation of 3x, which also gives 3, because constants differentiate to themselves.

  • What is the final expression obtained after differentiating the entire equation in the example?

    -The final expression obtained is (2x^2 + 3/x + 4x^3y)(dy/dx) = 14 - 4xy - 6x^2y^2.

  • What is the process to isolate dy/dx in the final expression?

    -To isolate dy/dx, factorize all terms involving x on one side and move the rest to the other side, then divide both sides by the expression containing x.

  • What is the final simplified form of dy/dx after solving the equation from the example?

    -The final simplified form of dy/dx is (14 - 4xy - 6x^2y^2) / (2x^2 + 3 + 4x^3y).

  • How can the numerator of the final expression be further simplified?

    -The numerator can be further simplified by dividing all terms by the common factor of 2, resulting in (7 - 2xy - 3x^2y^2).

  • What is the final answer after simplifying the expression for dy/dx?

    -The final answer after simplification is y/x = (7 - 2xy - 3x^2y^2) / (2x^2 + 3 + 4x^3y).

Outlines
00:00
📚 Introduction to Implicit Differentiation

The first paragraph introduces the concept of implicit differentiation, which is a method used when variables x and y are not explicitly expressed as functions of each other. The key idea is that both x and y are differentiated simultaneously. When differentiating with respect to x, the differentiation of y involves adding the term dy/dx. The paragraph provides an example equation with x and y terms combined and walks through the differentiation process, emphasizing the rule that when differentiating y, the dy/dx term is included.

05:00
🔍 Solving an Implicit Differentiation Problem

The second paragraph continues the discussion on implicit differentiation by applying the method to a specific example. It demonstrates the process of differentiating each term in the equation, factoring terms containing dy/dx to one side and moving other terms to the opposite side. The paragraph then simplifies the equation by factoring out common terms and dividing both sides by the remaining terms to isolate dy/dx. The final step involves simplifying the expression further to express y in terms of x, which is the goal of implicit differentiation.

Mindmap
Keywords
💡Implicit Differentiation
Implicit differentiation is a method used in calculus to differentiate equations that are not explicitly expressed as functions of x. It involves differentiating both x and y simultaneously. In the video, the instructor explains that while other differentiation methods involve expressing y as a function of x, implicit differentiation does not separate x and y, which is crucial for equations where y is not solely a function of x. An example from the script is the differentiation of 'x^2y + 3y + 2x^3y^2 = 14x', where both x and y are treated as variables to be differentiated.
💡Differentiate
To differentiate, in the context of calculus, means to find the derivative of a function with respect to a variable. The process involves applying rules of differentiation to determine the rate at which the function changes. In the script, the instructor demonstrates the differentiation of various terms within an equation, such as 'x^2' becoming '2x' when differentiated with respect to x.
💡dy/dx
The notation 'dy/dx' represents the derivative of y with respect to x, or the rate of change of y as x changes. It is a fundamental concept in calculus and is central to the method of implicit differentiation. In the video, the instructor emphasizes that when differentiating y, the term 'dy/dx' is included to account for the rate of change of y with respect to x.
💡Equation
An equation is a mathematical statement that asserts the equality of two expressions. In the context of the video, equations are used to represent relationships between variables, particularly x and y. The script involves differentiating a complex equation, 'x^2y + 3y + 2x^3y^2 = 14x', to understand how y changes with x.
💡Derivative
A derivative in calculus represents the rate at which a function is changing at a given point. It is a key concept in the study of functions and is used to analyze slopes of curves, among other applications. The video focuses on finding the derivative of y with respect to x using implicit differentiation, as shown when the instructor differentiates terms within the given equation.
💡Factorize
Factorization is the process of breaking down a polynomial or an expression into a product of its factors. It is a common technique used in algebra to simplify expressions. In the script, the instructor uses factorization to organize terms involving 'dy/dx' on one side of the equation and those without on the other, simplifying the final expression for 'dy/dx'.
💡Terms
In mathematics, terms are the individual elements of an algebraic expression, equation, or series. They can be numbers, variables, or expressions within an equation. The script discusses differentiating each term within a given equation using implicit differentiation, such as differentiating 'x^2y' and '3y'.
💡Simplify
Simplification in mathematics is the process of making an expression, equation, or function more straightforward or easier to understand without changing its value or meaning. In the video, the instructor simplifies the differentiated equation by moving terms around and factorizing to isolate 'dy/dx' and find its simplified form.
💡Variable
A variable is a symbol, often a letter, that represents a quantity in mathematics which can change or vary. In the context of the video, x and y are variables in the equation that are being differentiated. The process of implicit differentiation involves differentiating with respect to these variables simultaneously.
💡Expression
A mathematical expression is a combination of variables, constants, and operators (like addition, subtraction, multiplication, and division) that can be evaluated to give a single number. In the script, the instructor works with expressions such as 'x^2y' and '2x^3y^2', which are part of the equation being differentiated.
💡Rate of Change
The rate of change refers to how much one quantity changes relative to another. In calculus, this is often represented by derivatives and is a central theme in the video. The instructor is finding the rate at which y changes with respect to x (dy/dx) for the given equation, which is the essence of differentiation.
Highlights

Introduction to implicit differentiation, a method to differentiate equations where x and y are not separated.

Uniqueness of implicit differentiation lies in differentiating x and y simultaneously.

Differentiating y involves adding the term dy/dx, a key concept in implicit differentiation.

Example provided to illustrate the process of implicit differentiation.

Differentiating x terms remains the same, while differentiating y terms include dy/dx.

The equation 2x^2y + 3y + 2x^3 = 14x is used as a simple example for demonstration.

Differentiating each term of the equation step by step.

Resulting expression after differentiating is a combination of terms with and without dy/dx.

Terms without dy/dx are moved to the right side of the equation.

The final differentiated equation is isolated for dy/dx on one side.

Factorization of terms containing dy/dx is performed to simplify the equation.

Division by terms involving x is used to solve for dy/dx explicitly.

The final answer is expressed as y/x = (14 - 4xy - 6x^2y^3) / (2x^2 + 3 + 4x^3y).

Further simplification by factoring out common terms in the numerator.

The final simplified form of the derivative dy/dx is presented.

The process demonstrates the application of implicit differentiation in a clear, step-by-step manner.

The practical application of implicit differentiation for equations that are not easily separable into y as a function of x.

The importance of understanding the underlying concept of treating x and y as interconnected when differentiating implicitly.

Transcripts

Browse More Related Video

Implicit Differentiation

Math 11 - Section 3.8

Implicit Differentiation

Implicit Differentiation

Implicit Differentiation for Calculus - More Examples, #1

Implicit Differentiation for Calculus - More Examples #2

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Implicit DifferentiationMathematical FunctionsDifferentiation TechniquesEducational ContentMath TutorialX and Y VariablesDerivative CalculationAcademy LessonsMathematical AnalysisLearning ExcellenceAcademic Webinar