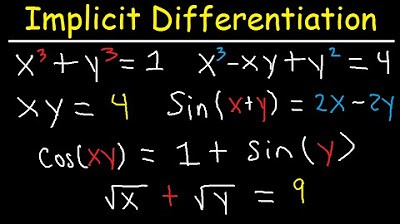Implicit Differentiation - Find The First & Second Derivatives
TLDRThe video script provides a comprehensive guide on implicit differentiation, a method used to find the derivative of a function that is not explicitly expressed in terms of a single variable. It begins with a basic example involving x^2 + y^3 - 4x = 8, illustrating the process of differentiating both sides with respect to x and isolating dy/dx. The script then moves on to more complex examples, including a problem with multiple y variables and another requiring the calculation of the second derivative. The use of the power rule, product rule, and quotient rule is explained, along with the steps to isolate dy/dx and d^2y/dx^2. The video concludes with an example that evaluates the second derivative at a specific point. The script is educational, offering additional resources for further learning and encouraging viewers to tackle more challenging problems involving trigonometric functions.
Takeaways
- 📚 Implicit differentiation is a method used to find the derivative of y with respect to x (dy/dx) when y is given implicitly as a function of x.
- 🔑 The power rule states that the derivative of x to the power of n is n times x to the power of n-1, which is crucial for differentiating terms like y^3.
- 📈 To differentiate an equation implicitly, differentiate every term with respect to x, treating y as a function of x, and use the chain rule when necessary.
- ⚖️ The constant term in an equation has a derivative of zero, simplifying the differentiation process.
- 🔄 To isolate dy/dx, manipulate the equation by moving terms without dy/dx to the other side and then dividing by the term containing y to simplify.
- 📝 For equations with multiple y variables, apply the product rule when differentiating terms involving both x and y.
- 🔍 Factor out dy/dx from terms in the equation to isolate it and solve for dy/dx.
- 🧩 When finding higher-order derivatives, like the second derivative (d²y/dx²), differentiate the first derivative equation with respect to x again, using the quotient rule if necessary.
- 📐 Evaluate the derivative at specific points by substituting the x and y values into the derived equation.
- 🔗 Additional resources for understanding basic derivative rules, such as the power rule, product rule, and quotient rule, are available in the video description.
- 🌟 For more complex problems involving trigonometric functions and implicit differentiation, further resources are provided in the video description for those interested in a challenge.
Q & A
What is the purpose of implicit differentiation?
-Implicit differentiation is used to find the derivative of a function that is not explicitly expressed in terms of y as a function of x. It is particularly useful when dealing with equations involving both x and y variables in a complex manner.
How do you differentiate x^2 with respect to x?
-The derivative of x^2 with respect to x is found using the power rule, which states that the derivative of x to the power of n is n times x to the power of n-1. Therefore, the derivative of x^2 is 2x.
What is the power rule in calculus?
-The power rule states that the derivative of x raised to the power of n (where n is a constant) is equal to n times x raised to the power of n minus 1, written as d/dx(x^n) = n*x^(n-1).
What is the derivative of a constant with respect to x?
-The derivative of any constant with respect to x is always zero because a constant does not change with respect to x.
How do you isolate dy/dx in an implicit differentiation problem?
-To isolate dy/dx, you need to collect all terms containing dy/dx on one side of the equation and all other terms on the opposite side. Then, divide by the coefficient of dy/dx to get it alone on one side of the equation.
What is the product rule in calculus?
-The product rule is used when differentiating a product of two functions. It states that the derivative of u*v is (v*du/dx) + (u*dv/dx), where u and v are functions of x, and du/dx and dv/dx are their respective derivatives.
How do you differentiate y^3 with respect to x?
-When differentiating y^3 with respect to x, you use the power rule and the chain rule. The derivative is 3y^2 times dy/dx, or 3y^2(dy/dx).
What is the quotient rule in calculus?
-The quotient rule states that the derivative of u/v is (v*du/dx - u*dv/dx) / v^2, where u and v are functions of x, and du/dx and dv/dx are their respective derivatives.
How do you find the second derivative of y with respect to x?
-To find the second derivative of y with respect to x, you first find the first derivative dy/dx, and then differentiate that result with respect to x again to get d^2y/dx^2.
What is the process to evaluate the second derivative at a specific point?
-To evaluate the second derivative at a specific point (x, y), you first find the expression for the second derivative d^2y/dx^2, and then substitute the x and y values of the point into this expression to calculate its value.
Why do you need to factor out terms when solving for dy/dx in implicit differentiation?
-Factoring out terms helps to isolate dy/dx on one side of the equation, making it easier to solve for dy/dx. It also simplifies the equation and can reveal a common factor that can be canceled out.
How can you use implicit differentiation to find higher order derivatives?
-You can use implicit differentiation to find higher order derivatives by differentiating the previously found derivative expressions with respect to x again, applying the appropriate rules such as the power rule, product rule, and quotient rule as needed.
Outlines
😀 Introduction to Implicit Differentiation
This paragraph introduces the concept of implicit differentiation. It begins with a problem involving x squared plus y cubed minus 4x equals eight and the task to find d y over dx. The process of differentiation is explained step by step, including the power rule and the differentiation of constants. The goal of isolating d y over dx is achieved by moving terms to either side of the equation and dividing by 3y squared, resulting in the final answer d y over dx equals 4 minus 2x divided by 3y squared. Additional resources for refreshing on basic derivative rules are also mentioned.
😀 Implicit Differentiation with Multiple Variables
In this paragraph, a problem involving y squared plus 5x squared y cubed plus x to the fourth equals nine is tackled using implicit differentiation. The process involves differentiating both sides of the equation with respect to x, applying the power rule, and utilizing the product rule for terms with multiple variables. Terms without d y over dx are moved to the other side of the equation, and d y over dx is factored out to isolate it. The final answer, d y over dx, is determined to be negative 4x cubed minus 10x y cubed divided by 2y plus 15x squared y squared.
😀 Finding the Second Derivative
This paragraph addresses finding the second derivative, d squared y over dx squared, using implicit differentiation. A problem involving x squared plus y squared equals 25 is given, with the goal to evaluate the second derivative at the point (4,3). The process involves differentiating both sides of the equation with respect to x, applying the quotient rule, and replacing d y over dx with its value. After simplification, the second derivative is found to be negative 25 over 27 when evaluated at the given point.
Mindmap
Keywords
💡Implicit Differentiation
💡Derivative
💡Power Rule
💡Product Rule
💡Quotient Rule
💡Chain Rule
💡Second Derivative
💡Constant
💡Isolation
💡Differentiation with Respect to x
💡Greatest Common Factor (GCF)
Highlights
The video introduces the concept of implicit differentiation and its application to solve problems involving functions of x and y.
The first example involves differentiating x^2 + y^3 - 4x = 8 to find dy/dx.
Derivatives of x^2 and y^3 with respect to x are derived using the power rule.
The constant term 8 has a derivative of 0, simplifying the equation.
Isolating dy/dx involves moving terms to one side of the equation and dividing by 3y^2.
The final expression for dy/dx in the first problem is (4 - 2x) / (3y^2).
The second problem involves a more complex equation with multiple y variables.
Differentiating y^2 and 5x^2y^3 using the product rule is demonstrated.
The process of isolating dy/dx by factoring and dividing is shown for the second problem.
The final expression for dy/dx in the second problem is (-4x^3 - 10xy^3) / (2y + 15x^2y^2).
The third problem focuses on finding the second derivative d²y/dx² of x^2 + y^2 = 25.
Differentiating both sides of the equation with respect to x and using the quotient rule is explained.
The second derivative d²y/dx² is found by substituting dy/dx back into the equation.
The value of the second derivative at the point (4,3) is calculated to be -25/27.
The video provides additional resources in the description for further understanding of derivatives.
The importance of understanding the power rule, product rule, and quotient rule for differentiation is emphasized.
The video concludes with an invitation to subscribe and access more complex problems involving implicit differentiation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: