💥💥💥Stuff You MUST Know Cold for the AP Calculus AB Exam💥💥💥[EVERYTHING YOU NEED TO KNOW] 2021
TLDRThe provided transcript is a comprehensive review for the AP Calculus exam, emphasizing the importance of memorizing formulas and theorems as no formula sheet is provided. The review covers key topics such as curve sketching, basic differentiation and antiderivatives, the application of various rules including the chain rule, product rule, and quotient rule, as well as the fundamental theorem of calculus. Additional areas of focus include the mean value theorem, approximation methods for integration like the trapezoidal rule, and the theorem of mean value and average value. The transcript also touches on solids of revolution, methods for calculating displacement and distance, and trigonometric identities. It concludes with a brief mention of L'Hôpital's rule and integration by parts, providing a solid foundation for students preparing for the AP Calculus exam.
Takeaways
- 📚 Remember that the AP Calculus exam does not provide a formula sheet, so you must know all the necessary theorems, differentiation, and integration rules by heart.
- 🔍 For curve sketching, ensure that y = f(x) is continuous, and be aware of critical points where the derivative is zero or undefined, and how to determine local minima, maxima, and points of inflection.
- 📉 Understand the basic differentiation rules, such as the power rule for x^n, and the derivatives of trigonometric functions like sine, cosine, and tangent.
- ∫ Learn the basic antiderivatives, for example, the antiderivative of x^n is x^(n+1)/(n+1), and the antiderivative of cosine is sine.
- 🔢 Know the rules for differentiating more complex functions, including the product rule, quotient rule, and chain rule, as well as how to apply L'Hôpital's rule for indeterminate forms.
- 📐 Be familiar with the Fundamental Theorem of Calculus, which connects differentiation and integration, and how to evaluate definite integrals.
- 🔴 Know how to apply the Mean Value Theorem and Rolle's Theorem, which are important for understanding the behavior of functions on a closed interval.
- 🔄 Understand the methods for approximating integrals, such as the trapezoidal rule, and be aware of the different techniques for solids of revolution like the disk, washer, and shell methods.
- 🚀 Be comfortable with the concepts of distance, velocity, and acceleration, and know the difference between displacement and distance traveled.
- 📈 Know common trigonometric function values for first quadrant angles and be familiar with trigonometric identities, such as double angle identities and power reducing formulas.
- 🧮 Be prepared to evaluate limits, especially those that result in indeterminate forms, using algebraic manipulation and L'Hôpital's rule.
Q & A
What is the key difference between the AP Calculus exam and other exams in terms of provided materials?
-The key difference is that the AP Calculus exam does not provide a formula sheet, so students must memorize all the necessary theorems, differentiation rules, and integration rules.
What is a critical point in calculus?
-A critical point is a point where the derivative is equal to zero or undefined. However, for it to be considered a local maximum or minimum, the derivative must also change sign as it passes over that point.
How does the second derivative test help in determining local extrema?
-The second derivative test states that if the second derivative is positive at a critical number, it implies a local minimum, and if the second derivative is negative, it implies a local maximum.
What is the basic rule for differentiating the function of sine?
-The derivative of sine is cosine. So, when differentiating sin(x), the result is cos(x).
What is the antiderivative of x to the power of n?
-The antiderivative of x to the power of n is x to the power of n plus one, divided by n plus one, plus the constant of integration C.
How does the trapezoid rule for integration work?
-The trapezoid rule is the average of the left-hand endpoint method and the right-hand endpoint method. It's a way to approximate the definite integral by summing the areas of trapezoids under the curve.
What is the fundamental theorem of calculus, and how does it relate to antiderivatives?
-The fundamental theorem of calculus states that the definite integral of a function f(x) from a to b is equal to the antiderivative of f(x) evaluated at b minus the antiderivative evaluated at a. It connects differentiation and integration, showing that integration can be reversed by differentiation.
What is the mean value theorem, and how does it apply to a function on a closed interval?
-The mean value theorem states that if a function is continuous on a closed interval and differentiable on the open interval, there exists at least one point c in the interval such that the derivative at c is equal to the average rate of change over the interval. This means the slope of the tangent line at c is equal to the slope of the secant line through the endpoints.
How is the average value of a function on an interval found using the average value theorem?
-The average value theorem states that if a function is continuous on a closed interval and differentiable on the open interval, there exists a number c in the interval such that the function value at c equals the definite integral of the function over the interval divided by the width of the interval. This means the average value of the function on the interval is attained at some point within the interval.
What is the difference between displacement and distance traveled, and how are they calculated?
-Displacement is the straight-line distance from the initial to the final position and is found by evaluating the position function at the endpoints and subtracting. Distance traveled is the total length of the path taken, which is found by integrating the absolute value of the velocity function over the time interval.
What is L'Hôpital's rule used for, and under what conditions can it be applied?
-L'Hôpital's rule is used for evaluating limits of indeterminate forms, such as 0/0 or ∞/∞. It can be applied when the direct substitution results in an indeterminate form, and it involves taking the derivative of the numerator and denominator and re-evaluating the limit.
Outlines
📚 AP Calculus Exam Preparation Overview
This paragraph introduces the start of the AP Calculus exam review, emphasizing the importance of memorizing formulas and theorems as the exam does not provide a formula sheet. It mentions the source of the PowerPoint, which was updated for the video's purpose, and begins a review of curve sketching and analysis, including the conditions for local minima, maxima, and points of inflection. Basic differentiation rules for various functions are also covered, along with antiderivative techniques and additional integrals.
🧮 Derivatives and Antiderivatives of Trigonometric Functions
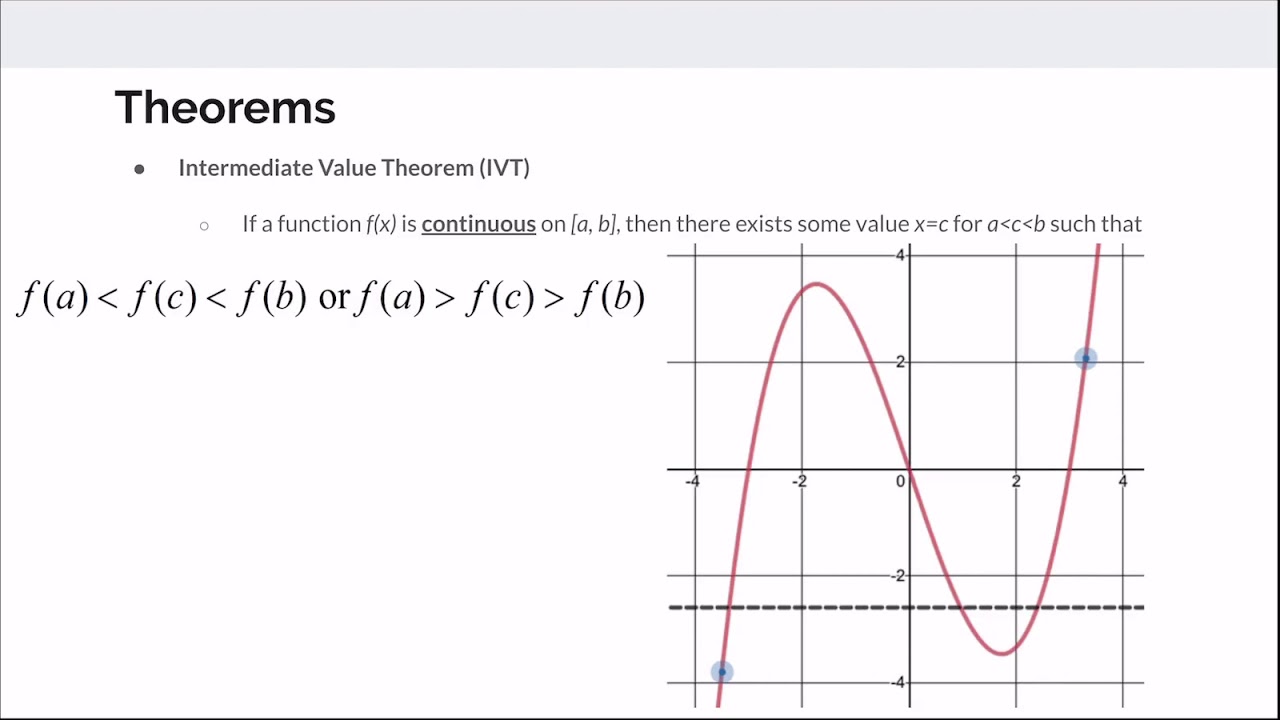
The second paragraph delves into the derivatives of inverse trigonometric functions and the derivatives of exponential and logarithmic functions. It continues with a discussion on differentiation rules such as the chain rule, product rule, and quotient rule. The fundamental theorem of calculus is introduced, which connects differentiation and integration. The paragraph also touches on the intermediate value theorem and the mean value theorem, explaining their significance in calculus.
🔍 Mean Value Theorems and Approximation Methods
This paragraph focuses on the mean value theorem and Rolle's theorem, explaining their relationship and applications in calculus. It then transitions into approximation methods for integration, specifically the trapezoidal rule, and clarifies that Simpson's rule is not tested on the AP exam. The concept of the average value theorem is introduced, which relates to the average height of a curve over an interval. Solids of revolution are discussed, with an emphasis on the disk, washer, and general methods for finding volumes.
📏 Distance, Velocity, and Acceleration Concepts
The fourth paragraph discusses the concepts of distance, velocity, and acceleration, highlighting the difference between displacement and distance traveled. It clarifies that displacement is found by integrating velocity over a time interval, while distance is the integral of the absolute value of velocity. The importance of understanding the shape of the cross-section in volume calculations is emphasized, and common mistakes in calculating the washer method are pointed out.
📐 Trigonometric Values and Identities
This paragraph provides a review of common values for trigonometric functions, stressing the need to know these values for both calculator and non-calculator portions of the AP exam. It also covers several trigonometric identities, including double angle identities, power reducing formulas, and the Pythagorean identity. The paragraph briefly introduces L'Hôpital's rule for evaluating limits of indeterminate forms, which is a new topic for the AP Calculus AB exam.
🧩 Integration by Parts and Final Review Notes
The final paragraph covers integration by parts, illustrating the process with an example using the natural logarithm function. It emphasizes the selection of u and dv in the integration by parts formula and provides a step-by-step calculation. The paragraph concludes with a brief mention of other topics such as vectors and average velocity, and it encourages students to reach out with any questions. It also wishes the students good luck on their upcoming exams.
Mindmap
Keywords
💡AP Calculus Exam
💡Derivative
💡Antiderivatives
💡Trigonometric Functions
💡Chain Rule
💡Product Rule
💡Quotient Rule
💡Mean Value Theorem
💡Rolle's Theorem
💡Integration by Parts
💡L'Hôpital's Rule
Highlights
AP Calculus exam does not provide a formula sheet, so students must memorize all necessary formulas and theorems.
Review of curve sketching and analysis, including the importance of checking endpoints and understanding changes in derivative signs for local minima and maxima.
Explanation of the second derivative test for determining local minima and maxima, as well as points of inflection.
Basic differentiation rules for functions such as x to the power of n, sine, cosine, and tangent.
Derivatives of inverse trigonometric functions and the use of cofunctions to simplify the process.
Integration techniques, including basic antiderivatives and the use of substitution methods.
Product, quotient, and chain rules for differentiation, with common mistakes to avoid.
Fundamental Theorem of Calculus linking differentiation and integration, and its implications.
Intermediate Value Theorem and Mean Value Theorem, with applications to function behavior on intervals.
Rolles Theorem as a specific case of the Mean Value Theorem, applicable when endpoints are equal.
Approximation methods for integration, such as the trapezoid rule, and when not to use Simpson's rule.
Average Value Theorem and its relation to the definite integral and the function's average height on an interval.
Solids of revolution and methods for calculating volumes, including disk, washer, and general volume formulas.
Differentiation in the context of physics, with emphasis on the relationship between position, velocity, and acceleration.
Concepts of displacement and distance traveled, and how to calculate each using integration.
Importance of understanding trigonometric identities and their utility in simplifying calculus problems.
Introduction of L'Hôpital's rule for evaluating limits of indeterminate forms, a new addition to the AP Calculus AB exam.
Integration by parts, presented as a reverse product rule, and its application in solving complex integrals.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: