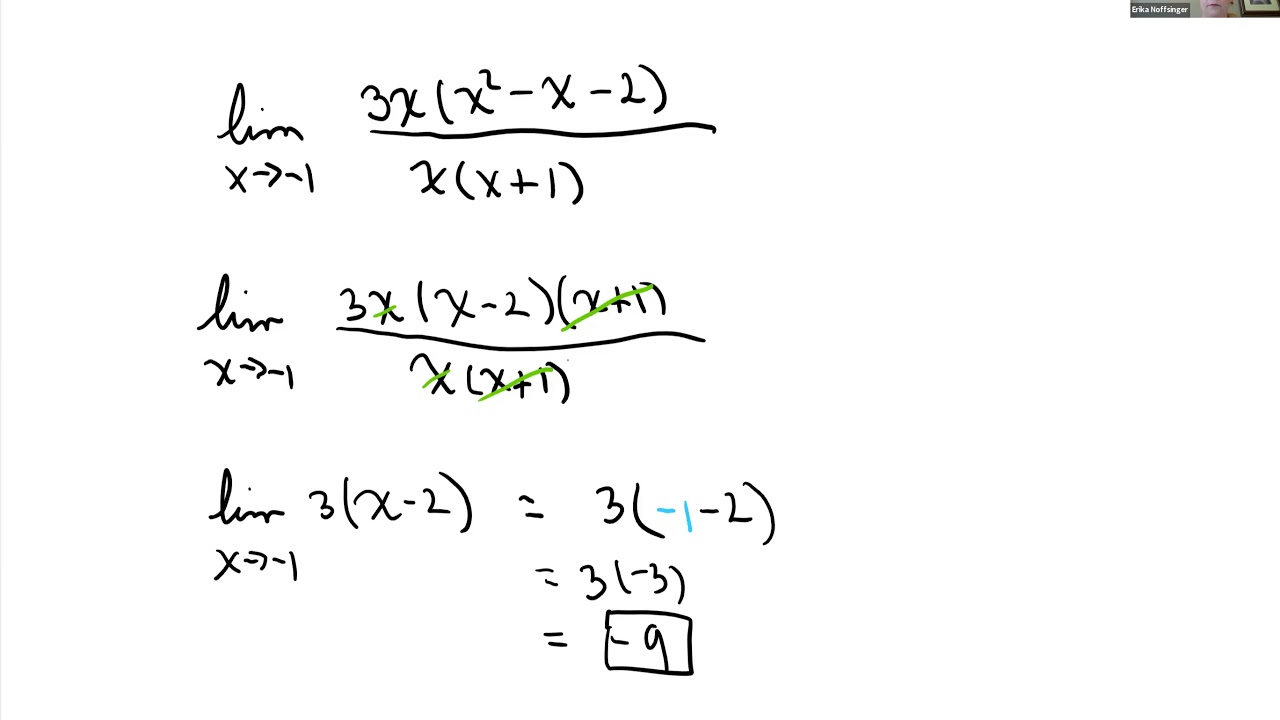Zoom session make up AP Calc Exam Review
TLDRThe video script is a comprehensive review session for an AP Calculus exam, focusing on derivatives, critical points, and integrals. It covers how to interpret derivative graphs, find absolute extrema, and apply u-substitution and chain rules. The instructor also discusses Riemann sums, the Mean Value Theorem, and l'Hôpital's rule, providing examples and practice problems. Additionally, the script touches on differential equations, slope fields, and submitting AP exam answers via email if there are technical issues.
Takeaways
- 📚 The session is focused on reviewing Sheet 7 for an AP exam, covering topics such as derivative graphs, Riemann sums, and their potential appearance on a makeup test.
- 🔍 The instructor emphasizes the importance of understanding major topics and being prepared for various versions of the test, given the differences in content across versions.
- 📈 The concept of 'G' as a continuous function with a domain between -8 and 12, composed of line segments, is introduced, with 'G' being derived from 'F' as G(x) = ∫ from -2 to F(t) dt.
- 📝 The process of finding critical points of 'G' on the given interval involves analyzing the slope and identifying relative maxima and minima from the derivative graph of 'G'.
- ⚖️ The task of finding G(-5), G'(-5), and G''(-5) involves evaluating areas under the graph, identifying y-values, and calculating slopes from the derivative graph.
- 📉 The instructor discusses identifying intervals where the graph of 'G' is both decreasing and concave up, using information from the first derivative graph to determine concavity.
- 🔑 The Extreme Value Theorem is highlighted for finding the absolute maximum value of 'G', which involves testing endpoints and relative maxima.
- 🧩 The session includes a problem involving u-substitution and the first fundamental theorem of calculus to evaluate a definite integral.
- 📊 The use of Riemann sums with four subintervals is demonstrated to estimate the definite integral of a function, using right endpoints to approximate the area under the curve.
- 🔄 The concept of finding a particular solution to a differential equation is covered, including the process of separation of variables and integrating both sides.
- 📐 The instructor discusses the properties of a slope field and how to identify inconsistencies with a given differential equation, such as undefined slopes and restrictions on x or y values.
Q & A
What topics are expected to be on the makeup AP exam based on the transcript?
-The topics expected to be on the makeup AP exam include derivatives, graphs of continuous functions, Riemann sums, and potentially differential equations.
What is the significance of the notation 'G(x) = ∫(−2 to x) F(t) dt' in the context of the transcript?
-This notation indicates that G(x) is the integral of F(t) from -2 to x, which means F(x) is the derivative of G(x), or G'(x) = F(x).
How does one find the x-coordinates of critical points of G on the open interval from negative 8 to 12?
-The x-coordinates of the critical points of G can be found by identifying where the slope of the function is zero, which corresponds to the x-intercepts on the graph of its derivative, G'(x).
What is the process for finding G(−5), G'(−5), and G''(−5) as described in the transcript?
-To find G(−5), evaluate the definite integral from -2 to -5 of F(t) dt. For G'(−5), find the y-value of F at x = -5. For G''(−5), determine the slope of the F graph at x = -5.
How can one determine if a function is concave up or concave down using its first derivative graph?
-A function is concave up where its first derivative graph has a positive slope, and concave down where it has a negative slope.
What is the Extreme Value Theorem, and how does it apply to finding the absolute max value of a function?
-The Extreme Value Theorem states that a continuous function on a closed interval attains its maximum and minimum values. To find the absolute max, test the endpoints and any relative maxima or minima.
What is the purpose of u-substitution in calculus, and how is it applied in the context of the transcript?
-U-substitution is used to simplify complex integrals that cannot be solved using standard rules. It involves replacing a part of the integrand with a new variable, simplifying the integral, and then reverting back to the original variable.
How does the concept of a tangent line relate to the derivative of a function?
-The derivative of a function at a given point gives the slope of the tangent line to the function's graph at that point. The equation of the tangent line can be found using the point-slope form of a line.
What is the meaning of M''(t) in the context of the transcript, and how is it used to approximate values?
-M''(t) represents the rate of change of the rate of cars left on the shelf, or the acceleration of the card depletion process. It is used to approximate values by considering the slope of the graph at certain points.
What is the role of Rolle's Theorem in the context of the transcript, and how does it apply to the function M(t)?
-Rolle's Theorem states that if a function is continuous on [a, b], differentiable on (a, b), and f(a) = f(b), then there exists at least one c in (a, b) such that f'(c) = 0. It is used to determine that there is a time between 4 and 7 when the rate of change of the card depletion is zero.
How is l'Hôpital's rule mentioned in the transcript, and what is its application?
-L'Hôpital's rule is used to evaluate limits of the form 0/0 or ∞/∞ by taking the limit of the ratio of the derivatives of the numerator and denominator. It is suspected to be applicable when the limit results in one of these indeterminate forms.
What is the significance of a slope field in the context of differential equations, and how is it analyzed in the transcript?
-A slope field represents the slopes of the tangent lines to the solutions of a differential equation at various points in the plane. It is analyzed by comparing the properties of the slope field with those expected from the differential equation to identify inconsistencies.
Outlines
📚 AP Exam Review: Derivatives and Riemann Sums
The instructor begins by outlining the topics for an upcoming makeup test, which may include derivatives and Riemann sums, based on previous AP exam questions. They emphasize the importance of having an overview of major topics for review. The focus then shifts to a specific problem involving the graph of a continuous function and its derivative, denoted as G'. The instructor guides students through identifying critical points of the function G on a given interval and understanding the relationship between the derivative graph and the original function's behavior.
🔍 Calculating Function Values and Derivatives
This section delves into calculating specific values of a function G and its derivatives using the provided derivative graph. The instructor explains how to find G(-5) by evaluating the area under the curve of G', and how to find G'(-5) and G''(-5) by reading the slope and second derivative from the graph. The process involves understanding the geometric interpretation of integrals and the concept of derivatives as slopes of the tangent line at a point.
📉 Analyzing Concavity and Extreme Values
The instructor moves on to analyze the concavity and extreme values of the function G. They explain how to identify intervals where the function is decreasing and concave up by examining the slope and concavity from the derivative graph. The extreme value theorem is introduced to find the absolute maximum value of the function within the given domain, which involves evaluating the function at critical points and endpoints.
📝 Worksheet 7: Derivative Applications
The instructor discusses worksheet 7, which includes problems on derivatives that appeared on a previous AP exam. They stress the importance of being comfortable with substitution and the first fundamental theorem of calculus for solving integrals. The summary includes a walkthrough of a problem involving the evaluation of a definite integral with a variable inside the function, demonstrating the process of u-substitution and adjusting bounds for integration.
🤔 Differentiation and Chain Rule
This part of the script focuses on the differentiation of composite functions, specifically finding the derivative of H(T) which is defined as the square root of another function f(X). The instructor uses the chain rule to find H'(T) and H'(10) by substituting the function values and slopes from the graph at the point of interest.
📉 Card Sales Dynamics and Tangent Line Approximation
The instructor presents a problem involving the rate of change in the number of greeting cards on a store shelf over time. They discuss how to approximate the second derivative, which represents the rate of change of the sales rate, using a table of values. The concept of the tangent line is introduced to approximate the number of cards left on the shelf at a specific time, and the instructor demonstrates how to write the equation of the tangent line at a given point.
🔍 Rolle's Theorem and L'Hôpital's Rule
The script explores the application of Rolle's Theorem to guarantee the existence of a point where the slope of a function is zero between two points with the same derivative values. The instructor also introduces L'Hôpital's Rule for indeterminate forms, demonstrating how to apply it to find limits involving 0/0 or ∞/∞ scenarios.
📚 Riemann Sums and Antiderivatives
The instructor discusses the use of Riemann sums to estimate the value of a definite integral, given a function and its rate of change over intervals. They also explain how to convert a second derivative into an antiderivative using the first fundamental theorem of calculus, allowing for the evaluation of the integral over a specific range.
🔄 Product Rule and Slope Fields
This section covers the application of the product rule to find the derivative of a product of two functions, using given values from a table and a graph. The instructor also addresses the concept of slope fields in differential equations, explaining how to identify inconsistencies between a given slope field and a proposed differential equation.
🤔 Differential Equations and Initial Conditions
The instructor works through a problem involving a first-order differential equation, demonstrating how to separate variables and solve for the antiderivative. They apply an initial condition to find the particular solution to the differential equation, highlighting the process of back-substitution and solving for the constant of integration.
📉 Second Derivatives and Linear Approximation
The script concludes with a discussion on finding second derivatives and using them to determine the concavity of a function. The instructor explains how the sign of the second derivative can indicate whether a linear approximation is an overestimation or an underestimation of the function's value at a given point.
📅 AP Exam Logistics and Preparation
In the final part of the script, the instructor addresses the logistics of the upcoming AP exam, including the process for submitting work via email if there are technical difficulties. They encourage students to review additional practice problems and express their readiness to answer individual questions, aiming to ensure that students are well-prepared for the exam.
Mindmap
Keywords
💡Derivative
💡Riemann Sums
💡Critical Points
💡Continuous Function
💡Definite Integral
💡Slope
💡Concavity
💡Absolute Maximum
💡U-Substitution
💡Product Rule
💡Tangent Line
Highlights
Discussion on preparing for a makeup test with potential topics such as derivative graphs and Riemann sums.
Explanation of the relationship between a function and its derivative graph, denoted as G' representing the derivative of G.
Method to find critical points of a function G by analyzing the slope and sign changes on the derivative graph.
Approach to find the x-coordinate of critical points using the concept of relative maxima and minima.
Process to calculate G of a specific value using the definite integral and geometric shapes on the graph.
Technique to find G' (derivative of G) and G'' (second derivative of G) for a given x value.
Identification of intervals where the graph of G is decreasing and concave up by analyzing the slope and concavity from the derivative graph.
Application of the Extreme Value Theorem to find the absolute maximum value of a function.
Use of u-substitution in evaluating a definite integral that involves a function within a function.
Conversion of bounds from x to u in a definite integral after u-substitution to match the function under the integral.
Finding H' (derivative of H) using the chain rule for a function composed of two other functions.
Interpretation of M' (derivative of M) from a table of values to understand the rate at which cards are leaving a shelf.
Approximation of M'' (second derivative of M) using nearby points and the concept of rates of change.
Writing the equation of a tangent line at a specific point using point-slope form and interpreting its meaning.
Application of Rolle's Theorem to find a time when the rate of change of cards leaving the shelf is zero.
Use of l'Hôpital's rule to evaluate a limit involving an indeterminate form of zero over zero.
Estimation of a definite integral using Riemann sums with a specified number of subintervals.
Differentiation of a complex function involving a square root and application of the chain rule.
Finding H' of a specific value by applying the product rule to a multiplication problem involving two functions.
Analysis of a slope field to determine if it corresponds to a given differential equation and identification of inconsistencies.
Solution of a differential equation with an initial condition using separation of variables and integration.
Determination of whether a linear approximation is an over or under approximation based on the sign of the second derivative.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: