What We Must Know for Calculus AB
TLDRThis video serves as a comprehensive review of essential calculus concepts for AP Calculus AB. It covers the fundamentals of limits, continuity, derivatives, and integrals, including key formulas and theorems such as the Intermediate Value Theorem, Mean Value Theorem, and the Fundamental Theorem of Calculus. The instructor also touches on more advanced topics like implicit differentiation, related rates, and differential equations, ensuring students are well-prepared for the AP exam.
Takeaways
- 📚 Start with Limits: Understanding when a limit exists (e.g., continuous functions or removable discontinuities) and when it doesn't (e.g., vertical asymptotes or conflicting one-sided limits) is crucial.
- 🔍 Continuity Definition: A function is continuous at a point if the limit of the function as x approaches that point equals the function's value at that point.
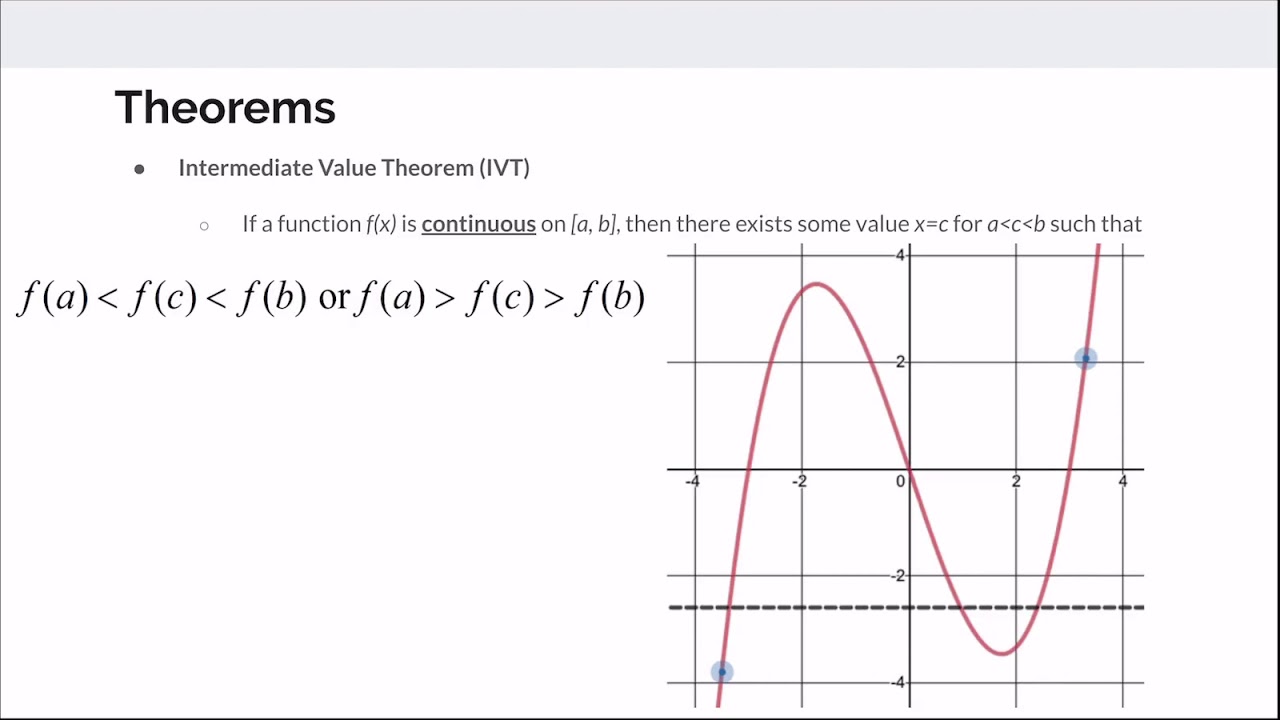
- 🌈 Intermediate Value Theorem: For continuous functions on a closed interval, if a certain y value lies between f(a) and f(b), there exists a c in that interval such that f(c) = y.
- 📈 Derivative Basics: Derivatives are defined as the limit of rise over run as run approaches zero, or as the slope of a curve at a given x value.
- 🔢 Power Rule: The derivative of x^n with respect to x is n * x^(n-1).
- 📉 Trigonometric Derivatives: Essential to know derivatives of sine, cosine, tangent, secant, cosecant, and cotangent.
- 🔠 Exponential and Log Derivatives: Key derivatives include e^x (derivative is e^x) and natural log (derivative is 1/x).
- 🔄 Chain Rule: For f(g(x)), the derivative is f'(g(x)) * g'(x).
- 🏔 Mean Value Theorem: If a function is differentiable on a closed interval and continuous on the open interval, its average rate of change equals its instantaneous rate of change at some point in the interval.
- 📊 Area Between Curves: The area between two curves is calculated by integrating the difference of the functions from a to b.
Q & A
What is the basic concept of a limit in calculus?
-A limit in calculus is said to exist if the one-sided limits as x approaches a certain point 'c' both exist and agree with each other. It can represent a continuous function or a removable discontinuity. A limit does not exist where the one-sided limits do not agree or where there is a vertical asymptote.
How is the continuity of a function defined?
-A function is continuous at a specific x value if the limit of the function as x approaches that value is equal to the value of the function at that point.
Can you explain the Intermediate Value Theorem?
-The Intermediate Value Theorem states that if a function is continuous on a closed interval and there is a y value between f(a) and f(b), then there exists some c between a and b such that f(c) equals the y value.
What is the definition of the derivative in calculus?
-The derivative is defined as the limit of the rise over run as the run approaches zero. It represents the slope of a curve at a given x value and can be expressed as the limit of (f(x) - f(c)) / (x - c) as x approaches c.
What is the Power Rule for derivatives?
-The Power Rule states that the derivative with respect to x of x to the nth power is n times x to the power of (n-1).
What are the derivatives of the basic trigonometric functions?
-The derivative of sine x is cosine x, and the derivative of cosine x is negative sine x. The derivatives of the other trigonometric functions like tangent, secant, cosecant, and cotangent are also important to know.
What is the derivative of the exponential function e^x?
-The derivative of e to the power of x is e to the power of x, which means it remains the same function.
How do you find the derivative of a function with a base other than e to the power of x?
-The derivative of a function like a^x (where a is a constant) can be found by rewriting a as e to the power of log(a) and then using the chain rule to take the derivative.
What is the Mean Value Theorem in calculus?
-The Mean Value Theorem states that if a function is differentiable on a closed interval and continuous on the open interval, then there exists some c in that interval where the average rate of change equals the instantaneous rate of change, expressed as f'(c) = (f(b) - f(a)) / (b - a).
What is the relationship between the derivative and the behavior of a function?
-The sign of the derivative indicates whether a function is increasing (positive) or decreasing (negative). The second derivative can indicate concavity, with positive values indicating concave up and negative values indicating concave down.
What is the significance of the second derivative test in determining extrema?
-The second derivative test can be used to determine if a critical point is a maximum, minimum, or neither by checking the concavity of the function. A positive second derivative at a point indicates a local minimum, while a negative second derivative indicates a local maximum.
How are volumes of solids of revolution calculated in calculus?
-Volumes of solids of revolution can be calculated using methods such as the disk method, washer method, and known cross-sections. These methods involve integrating the area of the cross-sections over the interval of revolution.
What is the Fundamental Theorem of Calculus and its application?
-The Fundamental Theorem of Calculus allows us to compute a definite integral by finding the net change in the antiderivative over the interval of integration. It is also applied in rectilinear motion problems to relate velocity and position.
What is the concept of average value in calculus?
-The average value of a function over a closed interval is the integral of the function over that interval divided by the length of the interval, expressed as (1 / (b - a)) * ∫[f(x) dx] from a to b.
What is the Second Fundamental Theorem of Calculus?
-The Second Fundamental Theorem of Calculus states that the derivative with respect to x of the integral from a to x of f(t) dt is f(x), where 'a' is a constant and 'x' replaces the dummy variable 't' in the integrand.
How do you calculate the area between two curves?
-The area between two curves is found by integrating the difference of the two functions from one point of intersection to the other, expressed as ∫[f(x) - g(x) dx] from a to b, where 'a' and 'b' are the x-values of the points of intersection.
Outlines
📚 Introduction to AP Calculus Review
This paragraph introduces the video's purpose, which is to remind viewers of the essential concepts they must know for AP Calculus. The speaker begins by discussing the concept of limits, emphasizing the importance of understanding when a limit exists or does not exist. They also cover the definition of continuity and the intermediate value theorem. The paragraph sets the stage for a comprehensive review of calculus topics, starting from the basics and progressing through more advanced concepts.
🔍 Derivatives and Their Applications
In this paragraph, the focus shifts to derivatives, starting with the definition of a derivative as a limit of the rise over run. The speaker explains the alternative definition of the derivative as the slope of a curve at a specific point. They then delve into derivative rules, including the power rule, trigonometric function derivatives, exponential and logarithmic derivatives, and derivatives of functions with bases other than e. The paragraph also covers derivative rules such as the product, quotient, and chain rules, as well as the derivative of the inverse function. The mean value theorem is briefly mentioned, highlighting its connection to the intermediate value theorem but with a focus on differentiability.
📈 Function Analysis and Implicit Differentiation
The speaker discusses function analysis, explaining how to draw conclusions about functions based on their derivatives. They introduce a three-column chart that categorizes functions as increasing or decreasing, concave up or down, and identifies points of inflection, maxima, and minima. Implicit differentiation is briefly mentioned, with an emphasis on practice rather than memorization. Related rates and geometry formulas, such as the area of a circle, volume of a cube, and circumference of a circle, are also discussed, though the speaker notes that these are generally provided in problems.
🧩 Differential Equations and Integrals
This paragraph covers differential equations, emphasizing the importance of separation of variables in finding particular solutions. The speaker warns that failing to use this method can result in losing significant points on free response questions. The discussion then moves to integrals, focusing on the fundamental theorem of calculus, which relates the computation of definite integrals to the net change in the antiderivative. The paragraph also touches on rectilinear motion, Riemann sums, and the average value of a function. The speaker provides a formula for finding an ending position given a starting position and a velocity function.
📐 Functions Defined by Integrals and Area/Volume Calculations
The final paragraph discusses functions defined by integrals, specifically the second fundamental theorem of calculus. The speaker explains how to differentiate an integral with respect to x by substituting the upper bound into the integrand. They also mention the need to multiply by the derivative when applying the chain rule. The paragraph concludes with a brief mention of area and volume calculations, including the area between two curves and volumes calculated by disks, washers, and known cross sections. The speaker acknowledges that while they did not cover volume in the current year, it is an essential topic for AP Calculus AB.
Mindmap
Keywords
💡Limits
💡Continuous Function
💡Intermediate Value Theorem
💡Derivatives
💡Power Rule
💡Trigonometric Derivatives
💡Exponential and Logarithmic Derivatives
💡Chain Rule
💡Mean Value Theorem
💡Implicit Differentiation
💡Differential Equations
💡Fundamental Theorem of Calculus
💡Volumes and Areas
Highlights
The importance of understanding limits, their existence, and non-existence, in the context of calculus.
The definition of a continuous function and the conditions required for a function to be considered continuous at a point.
The intermediate value theorem and its implications for continuous functions on a closed interval.
The concept of derivatives, their definition, and their role in determining the slope of a curve at any given point.
The power rule for differentiation and its application to polynomial functions.
Derivatives of trigonometric functions, including sine, cosine, tangent, secant, cosecant, and cotangent.
The derivatives of exponential functions and the special case of the derivative of e^x.
Derivatives of logarithmic functions, particularly the natural log, and how to handle exponentials with bases other than e.
Derivatives of inverse trigonometric functions and their significance in calculus.
The application of derivative rules such as the product rule, quotient rule, and chain rule.
The mean value theorem and its relation to the function's average rate of change over an interval.
Analyzing the behavior of functions using derivatives to determine increasing/decreasing intervals and concavity.
The process of finding maxima and minima using derivatives and the second derivative test.
The fundamental theorem of calculus and its application in computing definite integrals.
The relationship between velocity, acceleration, and position in the context of rectilinear motion.
The concept of Riemann sums and their use in estimating the area under a curve.
The calculation of average value of a function over a closed interval using integration.
The second fundamental theorem of calculus and its application in finding derivatives of integrals.
The process of solving applied problems using integration, such as finding displacement from velocity.
Volumes and areas in calculus, including the calculation of areas between curves and volumes using disks and washers.
Transcripts
Browse More Related Video

AP Calculus AB - 10 Minute Recap
AP Calculus AB Review

💥💥💥Stuff You MUST Know Cold for the AP Calculus AB Exam💥💥💥[EVERYTHING YOU NEED TO KNOW] 2021

AP Calculus Multiple Choice Practice Test (2020 AP CED Problems)

🚨EXPERT 🚨Tips for How to Get a 💥5 on the 2022 AP Calculus AB Exam💥 [What You REALLY Need to Know]

Calculus 1 Final Exam Review
5.0 / 5 (0 votes)
Thanks for rating: