AP Calculus Multiple Choice Practice Test (2016 AP CED Problems)
TLDRThe video script is a comprehensive guide for AP Calculus students preparing for their exams. It covers a variety of topics, including limit calculations, differentiation, and integration, with a focus on applying these concepts to multiple-choice questions. The instructor walks through 16 practice problems, starting with limits involving trigonometric functions and polynomials, then moving on to the application of L'Hôpital's rule, and the interpretation of derivatives in real-world contexts such as melting ice sculptures and room temperature changes. The guide also explores the mean value theorem, the calculation of average values over an interval, and the solution of differential equations. Each problem is accompanied by a detailed explanation, helping students understand not just the answers, but also the mathematical principles behind them. The summary concludes with a reminder of the importance of careful reading and learning from mistakes, emphasizing the value of practice for mastering AP Calculus concepts.
Takeaways
- 📚 Start with direct substitution when evaluating limits, but be ready to apply L'Hôpital's rule for indeterminate forms like 0/0 or ∞/∞.
- 🔍 For limits involving infinity, factor out the highest power of x from under radicals to simplify expressions before applying limits.
- 📈 When analyzing piecewise functions, pay attention to points of discontinuity and non-differentiability, as they are often the focus of multiple-choice questions.
- 🧊 For problems involving rates of change, such as the melting of an ice sculpture, use related rates and the chain rule to find the desired rate.
- 🔢 When matching a slope field to a differential equation, look for patterns like horizontal lines indicating where the derivative is zero.
- 📊 To find the average value of a function over an interval, divide the definite integral of the function over that interval by the length of the interval.
- 🤔 Be cautious with piecewise linear functions; ensure you understand the function's behavior at points of discontinuity when evaluating limits.
- 🧮 For definite integrals, ensure you use the correct delta x when approximating the integral, and use the right evaluation points for a Riemann sum.
- 🚗 When dealing with motion problems, integrate the acceleration function to find the velocity function, then integrate the velocity to find the displacement.
- 🏗️ For physics problems involving changing quantities, apply the appropriate calculus concepts, such as integration, to find the quantities of interest.
- 📉 Understand the implications of derivatives in context, such as how the rate of change (derivative) relates to the behavior of a function over time.
Q & A
What is the first step in solving the limit problem where the function is (cos(x) + sin(2x) + 1) / (x^2 - π^2) as x approaches π?
-The first step is to try direct substitution. Substitute π into the cosine function, which gives -1, and 2π into the sine function, which gives 0. This results in a numerator of 0 and a denominator of 0, indicating an indeterminate form.
What rule is applied to solve the indeterminate form 0/0 encountered in the first limit problem?
-L'Hôpital's Rule is applied to solve the indeterminate form 0/0. This involves taking the derivative of the numerator and the denominator and then re-evaluating the limit.
What is the alternative approach suggested for the second limit problem where the function is (sqrt(9x^4 + 1) / (x^2 - 3x + 5)) as x approaches infinity?
-The alternative approach is to factor out x^4 from everything inside the radical and then simplify the expression by dividing everything by x^2, the highest power of x in the denominator. This results in a limit that can be evaluated more directly.
In the third problem, what is the value of x that corresponds to a vertical tangent line on the graph of the piecewise-defined function?
-The value of x that corresponds to a vertical tangent line is x = -2. This is because a vertical tangent indicates an undefined derivative, but the function is still continuous at that point.
How is the rate at which the surface area of a sphere decreases related to the rate of decrease of its volume, given the volume decreases at a constant rate of 2π cubic meters per hour?
-The rate at which the surface area decreases (dS/dt) can be found using the surface area formula for a sphere (4πr^2) and the given rate of change of the volume (dV/dt = -2π). By using the chain rule and the relationship between volume and radius, we can find that dS/dt is -4π/5 square meters per hour when the radius is 5 meters.
What is the slope field shown in the fifth problem representing, and how can it be used to match with a differential equation?
-The slope field represents the instantaneous rate of change of a function at different points in its domain. It can be used to match with a differential equation by looking for horizontal lines, which indicate where the slope (derivative) is zero, and then factoring in the x and y variables to find the corresponding differential equation.
What is the correct interpretation of the statement 'F Prime of 3 equals two' in the context of the seventh problem?
-The statement 'F Prime of 3 equals two' means that the derivative of the function F at the point x = 3 is 2. This indicates the rate of change or the slope of the tangent line to the function F at x = 3 is 2.
In the eighth problem, how can you determine which of the given limits is equal to the integral from three to five of x to the fourth dx?
-To determine which limit is equal to the integral, you should look for the answer choice that correctly represents the function x to the fourth and the interval from three to five. The correct answer will use the right delta x, which is (5 - 3)/n, and will evaluate the integral using the correct evaluation point x sub k within the interval.
What is the average value of a continuous function f on the closed interval from negative four to four, as described in the ninth problem?
-The average value of a function on a given interval is calculated by taking the integral of the function over that interval and then dividing by the length of the interval. For the interval from -4 to 4, which is 8 units long, the average value is found by summing the areas of the geometric shapes formed by the function graph and dividing by 8.
In the tenth problem, what type of differential equation is given, and how is it solved?
-The given differential equation in the tenth problem is a separable differential equation. It is solved by separating the variables and integrating both sides. The solution involves exponentiating after integrating the natural logarithm and using the initial conditions provided to find the constants in the solution.
What does the expression 'H Prime of 5 equals two' represent in the context of the thirteenth problem, which models the temperature of a room after the thermostat is adjusted?
-The expression 'H Prime of 5 equals two' represents the rate of change of the room's temperature with respect to time, 5 minutes after the thermostat was adjusted. It means that the temperature is increasing at a rate of 2 degrees Fahrenheit per minute at that specific time.
In the fourteenth problem, what additional condition is necessary to guarantee that there is a number c in the open interval (2, 5) such that F Prime of c equals zero, given that f is continuous on the closed interval [2, 5]?
-The additional condition necessary is that the function f is differentiable in the open interval (2, 5). This is because the Mean Value Theorem, which guarantees the existence of a point c where the derivative is zero, requires the function to be differentiable on the open interval and continuous on the closed interval.
How is the height of the water in a rain barrel at time T equals two hours determined, given the rate of increase R of T as described in the fifteenth problem?
-The height of the water in the barrel at time T equals two hours is determined by integrating the rate of increase function R of T from T equals one hour to T equals two hours. This integration will give the total increase in the height of the water over that time period, which is then added to the initial height at T equals one hour.
What is the total distance traveled by a race car that is braking on a straight track, given the acceleration function a of T as described in the sixteenth problem?
-The total distance traveled by the race car while braking is found by first determining the velocity function V of T by integrating the acceleration function. Then, the distance is calculated by integrating the velocity function from the time the brakes are applied (T equals zero) until the car stops, which is found by determining when the velocity function equals zero.
Outlines
📚 AP Calculus Practice Problems Overview
This video script introduces a set of 16 AP Calculus multiple-choice practice problems. The problems are applicable to both AB and BC exams and are based on the 2016-17 curriculum framework by the College Board. The script suggests that these problems are still relevant for the upcoming May exam. The first problem involves finding the limit of a trigonometric function as x approaches Pi, which requires the application of L'Hôpital's rule after direct substitution results in an indeterminate form of 0/0. The second problem deals with the limit of a function as x approaches infinity, which is solved by simplifying the expression rather than applying L'Hôpital's rule. An alternative approach is also discussed for when x tends to positive infinity.
🔍 Analyzing Limits and Differential Equations
The script continues with various calculus problems. Problem three involves a piecewise-defined function with specific conditions for continuity and differentiability. The fourth problem concerns the rate of change of the surface area of a melting ice sculpture in the shape of a sphere, which is solved using related rates and the formula for the surface area of a sphere. The fifth problem is a multiple-choice question that matches a given slope field to a corresponding differential equation. The sixth problem involves a piecewise linear function, and the script discusses how to approach the limit from the left and right, emphasizing the importance of understanding the context of the problem. The seventh problem is an integral problem that requires the application of the second fundamental theorem of calculus to find the derivative of a function, which is then evaluated at a specific point. The eighth problem involves finding which of the given limits is equal to a definite integral, and the solution involves understanding the relationship between Riemann sums and definite integrals.
📈 Calculus Applications and Mean Value Theorem
The ninth problem asks for the average value of a function over a given interval, which is solved using the concept of average value and geometry. The tenth problem presents a differential equation, and the script explains how to solve for the function f(T) using separation of variables and exponentiation. The eleventh problem requires selecting the correct graph of a function based on the given graph of its derivative, which involves understanding the relationship between a function's derivative and its behavior. The twelfth problem involves finding the intervals where a function is decreasing, which is done by graphing the derivative and identifying where it is negative. The thirteenth problem is an interpretation question about the rate of change of a room's temperature, which is solved by understanding the context of the derivative in a real-world scenario. The fourteenth problem discusses the conditions under which the mean value theorem applies to a function that is continuous on a closed interval, and the solution involves recognizing the importance of differentiability for the mean value theorem to hold. The fifteenth problem is a calculus application involving the rate of water collection in a rain barrel during rainfall, which requires integrating the given rate function over a specific interval.
🏎️ Race Car Distance Traveled with Given Acceleration
The sixteenth and final problem involves a race car that is traveling on a straight track and comes to a stop with a given acceleration function. The task is to find the distance traveled by the car during the time it takes to stop. The solution involves finding the velocity function by integrating the acceleration function, determining the time it takes for the car to stop by finding when the velocity function equals zero, and then integrating the velocity function over the time interval to find the distance traveled. The script mentions that this problem is complex and may not be typical for an AP exam due to the number of steps involved.
Mindmap
Keywords
💡AP Calculus
💡Multiple Choice Questions
💡Direct Substitution
💡L'Hôpital's Rule
💡Piecewise Function
💡Surface Area and Volume
💡Differential Equations
💡Slope Field
💡Average Value
💡Separable Differential Equation
💡Derivative
Highlights
The video covers 16 AP Calculus multiple choice practice problems suitable for both AB and BC exams.
Problems are based on the 2016-17 curriculum framework by the College Board.
Direct substitution is the first method to attempt for limits, followed by L'Hôpital's rule if necessary.
For limits involving infinity, factoring can sometimes be a better approach than L'Hôpital's rule.
When a function has a vertical tangent, it is continuous but not differentiable at that point.
The rate at which a sphere's surface area decreases can be found using the surface area formula and the rate of change of the radius.
A slope field can be matched to a differential equation by looking for horizontal lines and factoring in the equation.
Piecewise linear functions can be graphed and analyzed to determine the truth of statements about limits and derivatives.
The second fundamental theorem of calculus is used to find the derivative of an integral function.
Estimating Δx is crucial for approximating definite integrals and matching them to correct answer choices.
The average value of a function on a closed interval is calculated by dividing the integral of the function by the length of the interval.
Solving differential equations can involve separating variables and integrating, as shown with a specific example.
The graph of a derivative can reveal information about the original function's critical points and behavior.
The interpretation of a derivative in context, such as the rate of temperature change in a room, is a common application question.
The mean value theorem is applicable when a function is continuous on a closed interval and differentiable on an open interval within it.
The height of water in a rain barrel can be calculated using integration, taking into account the rate of increase over time.
The distance a race car travels after braking can be found by integrating the velocity function over the time interval until it stops.
The video provides a comprehensive review of AP Calculus concepts with practical applications and problem-solving strategies.
Transcripts
Browse More Related Video

AP Calculus BC 2008 Multiple Choice (no calculator) - questions 1 - 28

AP Calculus BC 2003 Multiple Choice (calculator) - Questions 76 - 92

AP Calc AB & BC Practice MC Review Problems #6

AP Calculus Multiple Choice Practice Test (2020 AP CED Problems)
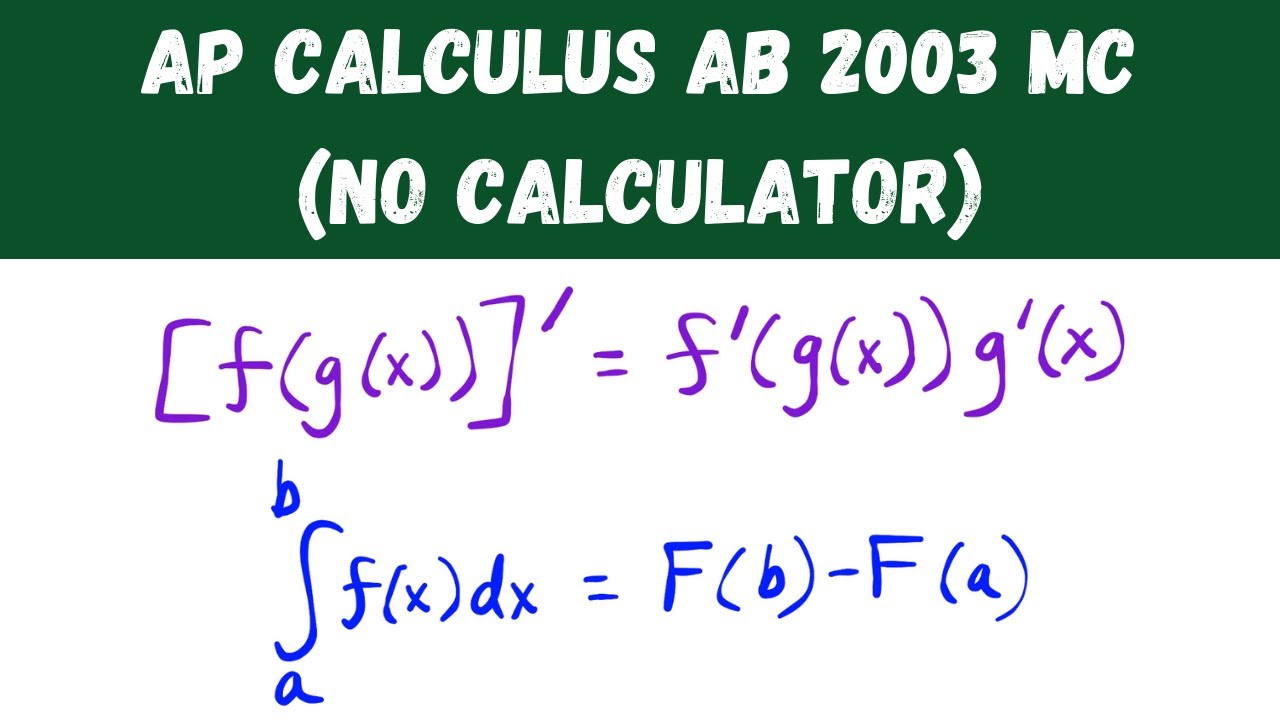
AP Calculus AB 2003 Multiple Choice (no calculator) - Questions 1-28

AP Calculus AB 2008 Multiple Choice (No Calculator)
5.0 / 5 (0 votes)
Thanks for rating: