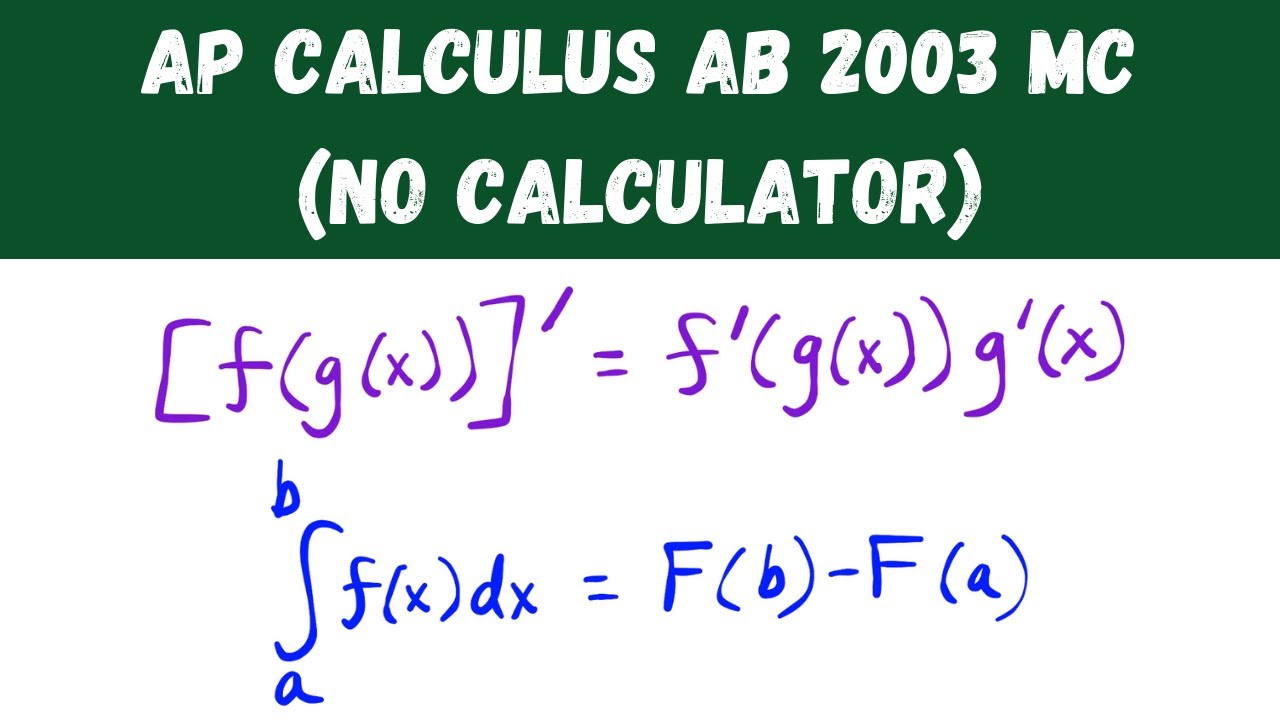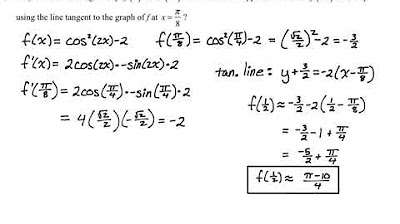AP Calculus AB Review
TLDRThe video script offers a comprehensive overview of key topics in AP Calculus AB, starting with limits and their role in defining continuity and differentiability. It delves into asymptotic behavior, including horizontal and vertical asymptotes, and the application of L'Hôpital's rule for indeterminate forms. The concept of derivatives is explored, highlighting their importance in determining the behavior of functions, including increasing/decreasing intervals and concavity. The Mean Value Theorem and Rolle's Theorem are introduced, emphasizing their significance in calculus. The video also covers the application of derivatives in real-world scenarios, such as optimization and related rates problems. The second part of the script transitions into integrals, discussing Riemann sums, the Fundamental Theorem of Calculus, and various integration techniques like u-substitution. It concludes with applications of integrals in areas such as average value, displacement, and differential equations, providing a well-rounded understanding of calculus concepts.
Takeaways
- 📌 Limits are a fundamental concept in calculus, used to describe the behavior of functions as they approach certain values.
- 📈 Horizontal and vertical asymptotes can be determined by examining limits as x approaches infinity or specific points, respectively.
- 🔄 L'Hôpital's rule is applied to indeterminate forms (0/0 or ∞/∞) by taking the derivative of the numerator and denominator separately.
- 🔶 Continuity and differentiability are key properties of functions, with differentiability implying continuity.
- 🔍 The Intermediate Value Theorem and Mean Value Theorem are important theorems that apply to continuous functions and have implications for the behavior of these functions.
- 📉 Derivatives are used to analyze the rate of change of functions, with the first derivative indicating increasing or decreasing behavior and the second derivative indicating concavity.
- 🏃 Position, velocity, and acceleration are interconnected concepts in physics that can be described using derivatives.
- 📊 Integrals represent the accumulation of change and can be approximated using Riemann sums, with the Fundamental Theorem of Calculus providing a method to find exact values.
- 🔢 Units in calculus problems are crucial and can help determine the type of quantity being described, such as rate of change or accumulated quantity.
- 🔍 The application of derivatives extends to optimization problems, where finding the maximum or minimum values of a function can be solved using the first and second derivative tests.
- 🧮 Techniques like u-substitution, long division, and completing the square are used to solve integrals, with attention to the limits of integration when applying u-substitution.
- 🔄 Related rates problems involve finding the rate of change of one quantity with respect to another, often requiring the use of implicit differentiation.
Q & A
What is the basic definition of a limit existing at a point C in the context of AP Calculus AB?
-The limit exists at a point C if the limit from the left equals the limit as X approaches from the right. This means that the function approaches the same value from both directions.
How can you determine the horizontal asymptote of a function when the degrees of the numerator and denominator are equal?
-In such cases, the horizontal asymptote is the ratio of the coefficients of the leading terms of the numerator and the denominator. This can also be found by applying L'Hôpital's rule multiple times.
What is the behavior of a function when the limit as X approaches a certain value does not exist?
-When the limit does not exist as X approaches a certain value, it either means the function is undefined at that point or the function tends towards positive or negative infinity.
Why is it important to check for continuity when discussing differentiability of a function?
-A function is differentiable only if it is continuous. Therefore, to ensure differentiability, one must first verify that the function is continuous, which includes checking that the limit from the left equals the limit from the right and equals the function's value at that point.
How does the Intermediate Value Theorem apply to a function that is differentiable?
-The Intermediate Value Theorem states that if a function is continuous on a closed interval, then it will take on every value between its minimum and maximum values within that interval. Since a differentiable function is also continuous, this theorem can be applied to it.
What is the Chain Rule in calculus and how is it applied?
-The Chain Rule is a method for finding the derivative of a composition of functions. It states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function, times the derivative of the inner function. It is applied by working from the outside in.
What is the significance of the second derivative in determining the concavity of a function?
-The second derivative test is used to determine if a function has a relative minimum or maximum at a given point. If the second derivative is positive at a point, the function is concave up (smiling) at that point, indicating a relative minimum. If the second derivative is negative, the function is concave down (frowning), indicating a relative maximum.
How does the concept of limits relate to the behavior of a function as it approaches vertical asymptotes?
-When approaching vertical asymptotes, the limit of the function either does not exist or it approaches positive or negative infinity. This is significant because it indicates a point where the function becomes undefined or the value of the function increases without bound.
What is the Mean Value Theorem and how does it relate to a function that is both continuous and differentiable?
-The Mean Value Theorem states that for a function that is continuous on a closed interval and differentiable on the open interval, there exists at least one point where the derivative of the function equals the average rate of change of the function over that interval. This theorem is applicable because it requires both continuity and differentiability.
How does the concept of linearization in calculus relate to the tangent line at a point on a curve?
-Linearization involves creating a linear approximation of a function near a specific point. This is done by using the point-slope form of a line, which is derived from the derivative (tangent line) at that point. It is a method to approximate the value of a function near the point where the derivative is known.
What is the Fundamental Theorem of Calculus and how does it connect differentiation and integration?
-The Fundamental Theorem of Calculus establishes the connection between differentiation and integration. It states that the integral of a function from a point 'a' to a point 'b' is equal to the antiderivative of the function evaluated from 'a' to 'b'. This theorem is crucial as it allows for the calculation of definite integrals by finding antiderivatives.
Outlines
📚 Introduction to AP Calculus AB: Limits and Continuity
Mr. Spinelli introduces key AP Calculus AB topics starting with limits, emphasizing the importance of limits from the left and right being equal at a point C for the limit to exist. He discusses asymptotic behavior, including horizontal asymptotes, and how to handle cases with equal degrees in the numerator and denominator. The concept of l'Hôpital's rule is introduced for indeterminate forms like 0/0 or ∞/∞. Vertical asymptotes are also explained, highlighting the non-existence of limits in certain cases. Continuity is discussed in relation to limits, and the concept of removable discontinuities is introduced with an example. The application of limits in determining the behavior of functions is emphasized throughout.
📈 Derivatives and Their Applications in Calculus
The paragraph delves into derivatives, starting with their definition as a limit and the transition from secant lines to tangent lines. The concept of instantaneous rate of change is introduced, and the standard notations and methods for finding derivatives are explained. Differentiability is discussed in the context of continuity, and the need to verify both function and its derivative's continuity. The Intermediate Value Theorem and the Mean Value Theorem are introduced with their conditions and implications. The importance of understanding derivatives in various contexts, such as physics and business, is highlighted, with a focus on the rules of derivatives, including power, quotient, and chain rules.
🔢 Derivatives and Their Practical Applications
The third paragraph focuses on the practical applications of derivatives, such as finding extrema (maxima and minima) using the first and second derivative tests. It explains the process of creating sign charts and the importance of checking endpoints for absolute extrema. The connection between derivatives and real-world phenomena like position, velocity, and acceleration is explored. The concept of inflection points and how to identify them using the second derivative is also discussed. The role of derivatives in determining the concavity and convexity of functions is highlighted, along with their use in optimization problems.
📉 Understanding the Fundamentals of Integration
Integration is introduced with an emphasis on approximating integrals using Riemann sums, including left, right, and midpoint methods. The importance of understanding the geometric interpretation of integrals as areas is stressed. The paragraph then transitions into the Fundamental Theorem of Calculus, which connects differentiation and integration. Techniques for evaluating integrals, such as u-substitution, are briefly mentioned. The applications of integrals in computing average values, total distance traveled, and understanding rates of change in related rates problems are discussed. The importance of considering units when performing integration and differentiation is highlighted.
🧮 Techniques of Integration and Their Applications
This paragraph explores various techniques of integration, such as Riemann sums, trapezoidal sums, and the use of summation notation. It also covers the Fundamental Theorem of Calculus in two parts, focusing on the relationship between antiderivatives and definite integrals. The concept of integration by parts is introduced, along with other methods like long division and completing the square. The paragraph concludes with a discussion on the applications of integrals, including calculating average values, position, velocity, acceleration, and total distance traveled. The importance of unit analysis in the context of integration and differentiation is emphasized.
🔁 Differential Equations and Their Solutions
The final paragraph focuses on differential equations, starting with the visualization of slope fields and the importance of lines of constant slope. It discusses how to sketch particular solutions through given points and the process of verifying solutions by plugging them into the original differential equation. The technique of separation of variables is explained, along with how to find both general and particular solutions using initial conditions. The importance of solving for the constant 'C' in the context of particular solutions is highlighted, and the viewer is wished good luck on their tests.
Mindmap
Keywords
💡Limits
💡Asymptotes
💡Continuity
💡L'Hôpital's Rule
💡Derivatives
💡Chain Rule
💡Implicit Differentiation
💡First and Second Derivative Tests
💡Integration
💡Applications of Derivatives
💡Differential Equations
Highlights
Limits are fundamental in AP Calculus AB, existing at a point C if the limit from the left equals the limit from the right.
Horizontal asymptotes can be determined by the limit of a function as X approaches positive or negative infinity, with special attention to degrees of the numerator and denominator.
L'Hôpital's rule is crucial for handling indeterminate forms like 0/0 or ∞/∞ by taking derivatives of the numerator and denominator separately.
Continuity in functions requires the limit to equal the function's value at a particular point, with special consideration given to removable discontinuities.
Derivatives are introduced as instantaneous rates of change, defined through limits and difference quotients.
The Mean Value Theorem states that for a continuous and differentiable function, there exists at least one point where the instantaneous rate of change equals the average rate of change over an interval.
Rolle's Theorem is a specific case of the Mean Value Theorem where the function values at the endpoints are equal, implying a point of zero slope exists within the interval.
Chain rule is a prevalent method in calculus for differentiating composite functions, working from the outside in.
Inverse functions are characterized by their composition resulting in the input variable X, with implications for derivatives and integrals.
Implicit differentiation is necessary when the function is not explicitly given in terms of y or x, requiring treating y as a function of x.
The first and second derivative tests are used to find local extrema and determine the concavity of functions.
Applications of derivatives include analyzing position, velocity, and acceleration in physics problems, connecting to the concept of rates of change.
Linearization involves writing a linear equation using a point and a slope, often in the point-slope form, for approximating functions.
Optimization problems often require expressing a function in terms of a single variable and finding its extrema using derivatives.
Related rates problems involve finding the rate of change of one quantity with respect to another, often using implicit differentiation and context clues.
Riemann sums and their approximations are essential for understanding the accumulation of change and the concept of integration.
The Fundamental Theorem of Calculus links antiderivatives with definite integrals, providing a method to find the exact area under a curve.
Techniques such as u-substitution, long division, and completing the square are used to solve integrals, with attention to changing limits of integration.
Integrals have practical applications in finding average values, total distance traveled, and solving problems involving rates and accumulation.
Differential equations are solved using various methods like slope fields, particular solutions, and separation of variables, with attention to initial conditions.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: