Limits
TLDRThe video script provides an in-depth lesson on the concept of limits in calculus. It explains that limits analyze the behavior of a function as the input (x-values) approaches a certain value, focusing on the output (y-values). The lesson covers various methods to determine limits, including graphical analysis, tables of values, and algebraic manipulation. The instructor emphasizes the importance of considering one-sided limits and the conditions under which a limit exists. The script also touches on limits at infinity, explaining how to determine the end behavior of a function. The lesson is practical, offering multiple approaches to finding limits, and encourages students to use the method that works best for them, whether it be algebraic, graphical, or through the use of a calculator.
Takeaways
- 📌 Understanding limits involves analyzing the behavior of a function as the input values approach a particular point.
- 📈 The independent variable (input) serves as a frame of reference, while the dependent variable (output) dictates the behavior being analyzed.
- ↔️ When determining limits, it is crucial to consider both one-sided limits (from the left and right) to confirm if a limit exists at a given point.
- 📊 Limits can be found using various methods: graphical analysis, tables of values, and algebraic manipulation.
- 🚫 A limit does not exist if the one-sided limits from the left and right are not equal.
- ∞ Limits at infinity (positive or negative) can be determined by understanding the end behavior of functions, which is akin to analyzing horizontal asymptotes.
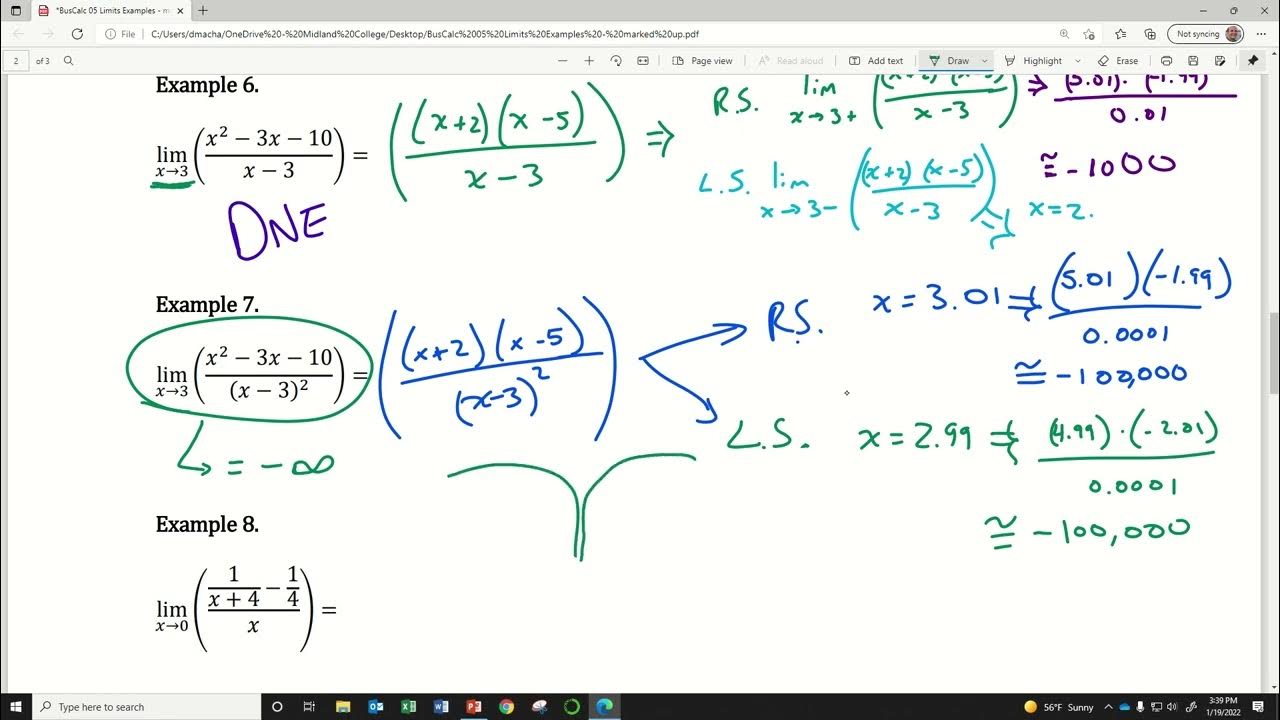
- 🔢 For functions with discontinuities or undefined points, algebraic manipulation can help find a simplified form that allows for the input of the point of interest.
- ✅ The limit of a function at a certain point is the value the function approaches as the input values get arbitrarily close to that point.
- 📐 The concept of limits is integral to calculus and is used to describe the behavior of functions, including at points of discontinuity.
- 🛠️ Rationalizing the numerator is a technique used in algebra to simplify fractions and allow for the input of values that would otherwise make the function undefined.
- 📉 For piecewise functions, the limit at a point where the function definition changes is found by evaluating the one-sided limits from both pieces.
Q & A
What is the fundamental concept of finding the limit of a function?
-The fundamental concept of finding the limit of a function is to analyze the behavior of the function as the input (independent variable) approaches a particular value. The behavior is determined by the output (dependent variable), which can be increasing, decreasing, positive, negative, or constant.
How do independent and dependent variables differ in the context of analyzing a function's behavior?
-Independent variables, often the inputs (like X values), serve as a frame of reference to locate where the analysis is taking place. Dependent variables, on the other hand, represent the outputs (like Y values), and it is their behavior (such as increasing, decreasing, or being positive/negative) that is the focus of the analysis.
What are the three common methods to find limits?
-The three common methods to find limits are: graphical analysis by observing the function's graph, creating a table of values to observe the behavior as the input approaches a certain value, and using an algebraic approach to simplify the function and directly calculate the limit.
What is a one-sided limit and how does it relate to the existence of a limit?
-A one-sided limit is the value that the function approaches as the input (X) approaches a certain value from either the left or the right side. For a limit to exist at a point, the one-sided limits from both the left and the right must converge to the same value.
What does it mean when the limit of a function as X approaches a certain value is said to be 'does not exist' (DNE)?
-When the limit of a function as X approaches a certain value is said to 'does not exist,' it means that the function does not approach a single, unique value as X gets arbitrarily close to that point from either side. This could be due to the function approaching different values from the left and right or because the function is undefined at that point.
How can you determine the limit of a function using an algebraic approach?
-Using an algebraic approach to determine the limit involves simplifying the function expression and then substituting the value of X the function is approaching. If the function cannot be directly substituted due to division by zero or other issues, algebraic manipulations like factoring, canceling common factors, or rationalizing the numerator/denominator may be required to find a substitutable expression.
What is a piecewise function and how does it affect the limit calculation?
-A piecewise function is a function that is defined by multiple sub-functions, each applicable over a certain interval of the domain. When calculating the limit of a piecewise function, one must consider the specific function definition that applies to the interval containing the point X is approaching. The one-sided limits must be calculated and checked for consistency to determine if the limit exists.
How does the behavior of a function as X approaches positive or negative infinity relate to the concept of end behaviors?
-The behavior of a function as X approaches positive or negative infinity is directly related to the concept of end behaviors. End behaviors describe the long-term behavior of a function as the inputs become extremely large or small. The limit at infinity is the value that the function's outputs approach or tend towards, which can be positive or negative infinity, a finite number, or it may not exist.
What is a horizontal asymptote and how does it affect the limit of a function as X approaches infinity?
-A horizontal asymptote is a horizontal line that a function approaches but never actually touches as X approaches infinity or negative infinity. It affects the limit by providing the y-value that the function's outputs approach as the inputs become extremely large or small. If a function has a horizontal asymptote, the limit of the function as X approaches infinity or negative infinity will be the y-value of that asymptote.
Why might one prefer using an algebraic approach over a graphical or table of values approach to find limits?
-One might prefer using an algebraic approach over a graphical or table of values approach because it can be more precise and does not rely on visual interpretation or approximation. It also avoids the need for graphing utilities and can be quicker for simple functions or when the function's behavior near the point of interest is algebraically straightforward.
What is the significance of factoring in simplifying a function to find a limit algebraically?
-Factoring is significant in simplifying a function to find a limit algebraically because it can help to eliminate common factors between the numerator and the denominator, which allows for cancellation. This simplification can make it possible to substitute the value of X the function is approaching, which is necessary for finding the limit directly.
Outlines
😀 Understanding Limits and Function Behavior
The paragraph introduces the concept of limits in the context of function behavior. It explains that when finding the limit of a function, we're analyzing the function's behavior as the input (independent variable, often denoted as X) approaches a certain value. The behavior is judged based on the output (dependent variable, often Y), considering aspects like increase, decrease, positivity, or negativity. The paragraph emphasizes the importance of the independent variable as a frame of reference and the dependent variable as the actual behavior under analysis. It also connects the concept to prior learning and uses examples to illustrate increasing, decreasing, and positive/negative behaviors of functions over specific intervals.
📈 Analyzing Function Behaviors: Increasing, Decreasing, and End Behaviors
This paragraph delves into specific behaviors of functions, such as increasing and decreasing, and how these are determined by examining the direction of the graph from left to right. It also discusses how to identify where a graph is positive or negative based on the sign of the Y values. The concept of end behaviors is introduced, which refers to the behavior of a function as the input approaches positive or negative infinity. The paragraph uses graphical examples to illustrate these behaviors, noting the presence of asymptotes and how they affect the function's end behavior.
🔢 Techniques for Finding Limits: Graphical, Tabular, and Algebraic
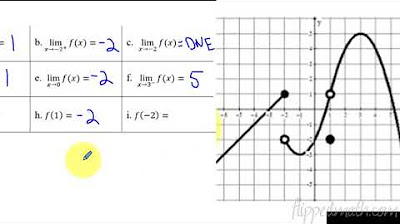
The paragraph explains three common methods for finding limits: graphical analysis, creating a table of values, and algebraic manipulation. It emphasizes that limits involve approaching a specific X value from both the left and right sides and that the function's Y values should converge to the same limit for the limit to exist. If the one-sided limits differ, the overall limit does not exist. The paragraph also touches on the concept of one-sided limits and how they are notated, indicating the direction of approach with a plus or minus sign above the X value.
📉 Limit Calculations with Graphical and Algebraic Approaches
The paragraph demonstrates how to find limits using both graphical and algebraic approaches. It shows how to analyze a graph to determine the limit by looking at the behavior of the function as it approaches a specific X value from the left and right. The algebraic approach involves substituting the X value into the function, provided it does not result in division by zero or other undefined operations. The paragraph provides examples of both approaches, illustrating how to determine if the function is approaching a specific Y value or if the limit does not exist due to differing one-sided limits.
🔍 Examining One-Sided Limits and Function Behavior at Discontinuities
This paragraph focuses on the scenario where a function is not defined at a certain point, such as a hole in the graph, and how to approach such points when finding limits. It explains that even if the function is not defined at a particular X value, it's still possible to find the limit by examining the behavior from the left and right. The paragraph also discusses how differing one-sided limits at a point indicate that the overall limit does not exist at that point.
🧮 Advanced Algebraic Limit Calculations and Rationalization
The paragraph explores more complex algebraic techniques for finding limits, particularly when direct substitution is not possible due to the function's form. It covers the method of factoring expressions and canceling common factors to simplify the function, making it possible to evaluate the limit. Additionally, the concept of rationalizing the numerator is introduced to deal with square roots or other complex expressions in the function. The paragraph provides examples of how to manipulate the function algebraically to find the limit as X approaches a certain value.
📊 Limits of Piecewise Functions and Behavior at Infinity
The paragraph discusses the concept of limits with piecewise functions, which have different expressions for different intervals of X values. It explains how to find one-sided limits and ensure they are the same on both sides of a discontinuity to determine the limit at a point. Additionally, the behavior of functions as X approaches positive or negative infinity is revisited, relating it to end behaviors previously discussed. The paragraph also provides graphical examples to illustrate these concepts.
∞ Limits at Infinity for Polynomial and Rational Functions
The final paragraph focuses on finding limits as X approaches positive or negative infinity for polynomial and rational functions. It explains that the behavior at these points is determined by the function's degree and the direction of approach. The paragraph provides a general approach to identifying the end behavior and thus the limit at infinity. It also mentions the use of a calculator or graphing tool for those who may not be familiar with the behavior of specific types of functions at infinity.
Mindmap
Keywords
💡Limit
💡Function
💡Independent Variable
💡Dependent Variable
💡End Behavior
💡One-Sided Limits
💡Graph
💡Table of Values
💡Algebraic Approach
💡Horizontal Asymptote
💡Undefined
Highlights
The concept of limits in calculus is introduced as a method to analyze the behavior of a function.
Behavior of a function is analyzed by considering both inputs (independent variables) and outputs (dependent variables).
The independent variable (input) serves as a frame of reference, while the dependent variable (output) shows the actual behavior.
Increasing, decreasing, and constant behaviors of functions are described in relation to the outputs (y-values).
The behavior of a function can be analyzed graphically, using a table of values, or algebraically.
One-sided limits are used to determine if a limit exists by approaching a value from the left and right.
If one-sided limits from both sides converge to the same value, the overall limit exists; otherwise, it does not (denoted as DNE).
Examples are provided to illustrate how to find limits using graphical analysis, table of values, and algebraic manipulation.
The algebraic approach to finding limits involves simplifying functions and plugging in the value the function approaches.
Rational functions are simplified by factoring and canceling out common terms to find limits algebraically.
Rationalizing the numerator is a technique used to handle indeterminate forms and find limits algebraically.
Piecewise functions require analyzing one-sided limits to determine the behavior as the input approaches different values.
End behaviors of functions as the input approaches infinity or negative infinity are also considered as limits.
Horizontal and vertical asymptotes are key features in determining the end behaviors and limits of rational functions.
The use of technology, such as graphing calculators, is encouraged for visualizing functions and their limits.
The importance of understanding the behavior of functions at specific points and at infinity is emphasized for a comprehensive understanding of limits.
The lesson provides a variety of tools and methods for students to find limits, catering to different preferences and levels of algebraic comfort.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: