Limits! Part 1
TLDRThis engaging video script introduces the concept of limits in calculus through a graphical approach. The presenter uses the hiking example of Amy and Joe to illustrate the idea of limits, explaining how their meeting point represents the common value where the function's behavior from the left and right converges. The script continues with mathematical examples, demonstrating how to estimate the y-value of a function as x approaches a certain point. It emphasizes the importance of the x-value in determining the limit and introduces the terms 'left-hand limit' and 'right-hand limit'. The video clarifies that a true limit exists only when both left and right limits agree, which may or may not coincide with the actual function value at that point. The script also addresses the behavior of limits around vertical asymptotes, highlighting the need for precision when dealing with infinite values. The presenter concludes with key takeaways, stressing the significance of estimating the y-value based on surrounding points and the conditions under which a limit exists, providing a solid foundation for further exploration into the algebraic side of limits.
Takeaways
- 📈 The concept of limits in calculus is introduced graphically, focusing on what the y-value should be at a certain x-value based on surrounding points.
- 🧗♀️ An analogy of hikers Amy and Joe meeting at a certain point illustrates the idea of a limit, where they both reach the same elevation.
- 📊 Limits are estimated by looking at the behavior of the function from both the left and right sides of the point in question.
- 🔢 Mathematically, the limit is written as 'lim(f(x)) as x approaches a certain value', which denotes the y-value the function approaches.
- 🔄 The process of estimating a limit involves observing the trend of y-values as x approaches the point from both directions.
- ↔️ A limit exists only if the left-hand limit and the right-hand limit agree on a common y-value.
- ❌ If the left-hand and right-hand limits do not match, the limit does not exist, indicating a discontinuity or an undefined behavior at that point.
- ➡️ The left-hand limit is denoted with a negative superscript, while the right-hand limit is denoted with a positive superscript next to the x-value.
- ∞ When dealing with vertical asymptotes, the limit does not exist if the function approaches infinity from either side, even if both sides approach the same type of infinity.
- 📍 The specific x-value is crucial when determining the limit, as it dictates from which sides the estimations are made.
- 🚫 The actual function value at a point may differ from the limit, especially at points of discontinuity, and the limit is about the estimated y-value, not the actual function output.
Q & A
What is the main topic of the video?
-The main topic of the video is the concept of limits in calculus, specifically focusing on understanding limits graphically.
What example is used to illustrate the idea of limits?
-The video uses a hiking example involving two hikers, Amy and Joe, to illustrate the idea of limits and how they meet at a common elevation.
What is the mathematical notation used to represent a limit?
-The mathematical notation for a limit is 'lim', which stands for 'limit', and is used as 'lim (f(x)) as x approaches C', where C is the value we are interested in.
What are left-hand and right-hand limits?
-Left-hand and right-hand limits are the values that a function approaches from the left and right sides of a point, respectively. They are denoted as 'lim (f(x)) as x approaches C from the left' and 'lim (f(x)) as x approaches C from the right'.
Under what condition does the limit of a function exist at a point?
-The limit of a function exists at a point if and only if the left-hand limit and the right-hand limit at that point are equal.
What does it mean if the left-hand and right-hand limits do not agree?
-If the left-hand and right-hand limits do not agree, it means that the full limit does not exist at that point, as there is no common value that the function approaches from both sides.
What is the relationship between the limit of a function and the function's actual value at a point?
-The limit of a function at a point is an estimate of what the function's value should be based on the surrounding points, and it may or may not be equal to the actual function value at that point.
What is a vertical asymptote and how does it affect the limit of a function?
-A vertical asymptote is a vertical line that the function approaches but never actually reaches. It affects the limit by causing the function to tend towards infinity or negative infinity as it approaches the asymptote from either side, resulting in a non-existent limit.
Why is the x-value important when computing a limit?
-The x-value is important because it determines the point from which the function's behavior is being analyzed. Different x-values can lead to different limits, even for the same function.
How does the video script use the Mean Girls joke to explain a concept in limits?
-The video script uses the Mean Girls joke to illustrate the idea that for a limit to exist (i.e., for 'fetch' to be successfully defined), both sides (left and right) must agree, just like in the movie where both the popular girls and the rest of the school have to agree on what 'fetch' means.
What is the criterion for the existence of a full limit?
-The criterion for the existence of a full limit is that the left-hand limit and the right-hand limit must be equal. If they are not equal, or if the function tends towards infinity from either side without being consistent, the full limit does not exist.
Outlines
📈 Introduction to Limits in Calculus
The video begins by introducing the concept of limits in calculus, focusing on a graphical understanding before moving on to algebraic explanations. The presenter uses a hiking analogy with two hikers, Amy and Joe, to illustrate how limits can be visualized by observing the graph and estimating the meeting point based on the values from both sides. The idea of a limit is defined as a common value where the function approaches from the left and right, which is graphically represented as the point where Amy and Joe meet at an elevation of 420 meters. The concept is further explored through a mathematical example, where the behavior of a function around a specific point (x = 1/2) is analyzed to determine the y-value that should be assigned to that point based on surrounding points. The video emphasizes that limits are about estimation and prediction, not the actual function value.
🔍 Estimating Limits and Existence of Limits
This paragraph delves deeper into the process of estimating limits by examining a function as X approaches the value of 3. The presenter explains that the Y value is estimated by looking at the behavior of the function from both the left and right sides of the point in question. When the estimates from both sides do not align, the limit is said not to exist. The concept of left-handed and right-handed limits is introduced, denoting the estimated Y values when approaching the point from the left and right, respectively. The video clarifies that a real limit exists only when both left and right limits are equal, and this is a critical criterion for determining the existence of a limit. The presenter also touches on the distinction between the limit of a function and its actual function value at a given point, noting that they may not always be the same.
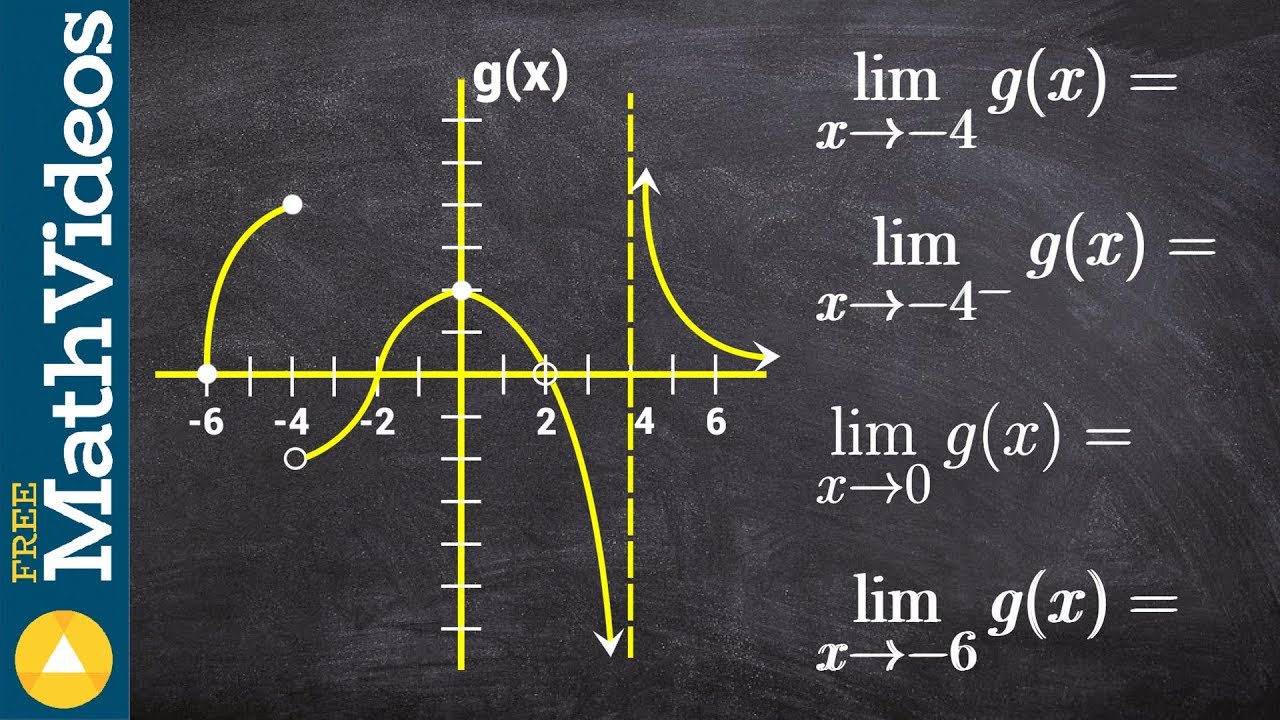
🚫 Understanding Non-Existence of Limits and Vertical Asymptotes
The final paragraph addresses the scenarios where limits do not exist, particularly when the function has vertical asymptotes. The presenter discusses three specific cases: approaching X equals 2, X equals 0, and X equals 7. For X approaching 2, the function tends towards negative infinity from the left and positive infinity from the right, indicating that the limit does not exist. When X approaches 0, both left and right estimates converge on a Y value of 0, confirming the limit's existence. Lastly, for X approaching 7, despite both sides suggesting the function tends towards infinity, the video emphasizes that the limit does not exist because it does not result in a finite value. The presenter stresses the importance of focusing on the X value when computing limits, as it significantly influences the outcome. The video concludes with a reminder of the key points: the limit is an estimation based on surrounding points, the X value is crucial, and the full limit exists only if the left and right limits agree.
Mindmap
Keywords
💡Limits
💡Graphical Interpretation
💡Left Hand Limit
💡Right Hand Limit
💡Vertical Asymptotes
💡Function Value
💡Estimation
💡Hiking Example
💡XY Chart
💡Mean Value
💡Existence of Limits
Highlights
The video introduces the concept of limits in calculus, focusing on a graphical understanding.
Uses a hiking analogy with Amy and Joe to illustrate the idea of limits.
Explains that the limit is a common value based on estimations from the left and right sides of a point.
Demonstrates how to estimate the y-value of a function graphically as x approaches a certain value.
Discusses the mathematical notation for finding limits and what it signifies.
Introduces the concept of left-handed and right-handed limits and their importance in determining the existence of a limit.
Explains that a real limit exists only if the left and right limits agree.
Clarifies that a limit does not necessarily equate to the actual function value at a given point.
Provides an example involving vertical asymptotes to show how limits are affected by the x-value.
Stresses the importance of focusing on the x-value when computing limits.
Details how to handle cases where the function approaches infinity on one or both sides.
Emphasizes that the limit does not exist if the function approaches different infinities on either side of a point.
The video concludes with a summary of the key points about limits and their graphical interpretation.
Highlights the importance of estimating from both sides and the role of the x-value in determining the limit.
Provides a clear criterion for when a limit exists: the left-hand limit must equal the right-hand limit.
Warns about the potential pitfalls of using the term 'infinity' without specifying direction.
Encourages viewers to stay tuned for the next video, which will cover the algebraic side of limits.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: