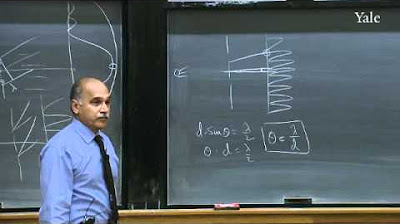The SIMPLEST Explanation of QUANTUM MECHANICS in the Universe!
TLDRThe video script offers a concise history and explanation of quantum mechanics, highlighting its fundamental concepts such as wave-particle duality, the Schrödinger equation, and the measurement problem. It emphasizes the probabilistic nature of quantum objects, the uncertainty principle, and entanglement, contrasting the quantum world with our macroscopic experience. The script also promotes two courses on Brilliant.org that delve deeper into quantum mechanics, inviting viewers to explore the subject further.
Takeaways
- 📚 Quantum mechanics was developed to explain phenomena that classical mechanics could not, such as how electrons orbit atoms without radiating energy and crashing into the nucleus.
- 🌀 Niels Bohr introduced quantized orbits to solve the problem of electron stability in atoms, which are proportional to Planck's constant.
- 🌊 Louis de Broglie proposed that if quantized orbits exist, electrons must be waves, a concept later supported by experiments showing interference patterns.
- 🌟 Erwin Schrodinger developed the Schrödinger Equation to describe the evolution of quantum waves over time.
- 🔍 The wave-particle duality presents a conundrum as quantum objects are detected as particles, not waves, despite their wave-like behavior.
- 🎲 Max Born suggested interpreting the wave function from the Schrödinger Equation as a probability distribution, which allows for a statistical description of quantum objects.
- 🔬 The measurement problem in quantum mechanics refers to the unexplained process of how a wave function collapses to a particle upon observation.
- 🚫 The lack of a clear understanding of wave collapse has not hindered the predictive success of quantum mechanics, but it remains a fundamental issue to be resolved for a complete understanding of the universe.
- 📊 The Uncertainty Principle states that it is impossible to know both the exact position and momentum of a quantum object simultaneously due to its probabilistic nature.
- 🔗 Quantum entanglement demonstrates strange correlations between particles, which Einstein referred to as 'spooky action at a distance,' but does not imply faster-than-light communication.
- ⚙️ Quantum mechanics reveals that the universe is quantized, with familiar quantities like energy, momentum, and electric charge occurring in discrete units, unlike the continuous nature of the macro world.
Q & A
What was the issue with classical mechanics in describing electron behavior around an atom?
-Classical mechanics failed to explain how an electron could orbit an atom without radiating energy and eventually crashing into the nucleus, as an accelerating charge like an electron would constantly lose energy according to Maxwell's classical equations.
How did Niels Bohr address the problem of electrons radiating energy while orbiting an atom?
-Niels Bohr proposed that electrons could exist without radiating energy if they rotated in quantized orbits proportional to Planck’s constant, thus avoiding the energy loss predicted by classical mechanics.
What did Louis de Broglie's research contribute to the understanding of electrons and quantum particles?
-Louis de Broglie showed that if quantized orbits exist for electrons, then electrons must be waves, which was further supported by experiments showing that all quantum particles exhibit wave-like interference patterns.
What is the significance of the Schrödinger equation in quantum mechanics?
-The Schrödinger equation, developed by Erwin Schrödinger, explains the wave-like behavior of quantum particles and describes how a wave evolves over time, providing a mathematical model for their behavior.
How does the detection of quantum objects present a conundrum in understanding their nature?
-The conundrum arises because experiments like the double-slit experiment suggest that quantum objects behave as waves, but when detected, they are observed as particles, leading to the challenge of reconciling their wave-particle duality.
What is the interpretation proposed by Max Born to resolve the wave-particle duality conundrum?
-Max Born suggested interpreting the wave determined by the Schrödinger equation as a probability wave, which allows a single quantum object to be described as a wave with a probability distribution of locations rather than having a distinct position.
What is the 'measurement problem' in quantum mechanics?
-The measurement problem refers to the unresolved issue of how or why the wave function collapses into a localized state upon measurement, transforming a quantum object from a wave-like to a particle-like state, which is not explained by the current quantum mechanics theory.
Why is the measurement problem considered a fundamental issue in quantum mechanics?
-The measurement problem is fundamental because it involves understanding how the quantum world interacts with our macroscopic world during measurement, which is essential for obtaining information about quantum objects. Without a resolution, we cannot have a complete understanding of the quantum realm.
What does the Uncertainty Principle state, and what are its implications?
-The Uncertainty Principle states that it is impossible to know both the exact position and momentum of a quantum object simultaneously. This principle highlights the probabilistic nature of quantum mechanics and has profound implications for our understanding of the fundamental nature of reality.
How do macroscopic objects like basketballs and dust particles relate to quantum mechanics?
-Macroscopic objects also exhibit wave-like behavior according to quantum mechanics, but their wavelengths are so small compared to their physical size that their quantum properties are not observable in everyday experiences. This is due to the large momentum of these objects making their de Broglie wavelengths extremely short.
What is the concept of 'entanglement' in quantum mechanics, and why is it significant?
-Entanglement is a phenomenon where multiple particles become correlated in such a way that the state of one particle is dependent on the state of another, even at large distances. This leads to 'spooky action at a distance' as described by Einstein and challenges our understanding of locality and information transfer in the universe.
How does the quantization of properties like energy and momentum affect our understanding of the universe?
-Quantization implies that familiar quantities such as energy, momentum, and electric charge occur in discrete units, rather than being continuous. This fundamental aspect of quantum mechanics reveals that the universe operates in distinct, quantized states, which is different from the continuous nature of classical physics.
Outlines
🌌 Introduction to Quantum Mechanics and its History
This paragraph introduces the topic of quantum mechanics by providing a brief historical overview of its development. It starts with the limitations of classical mechanics in explaining electron behavior around the nucleus without radiating energy. Niels Bohr introduced quantized orbits to solve this, and Louis de Broglie later suggested that electrons, and all quantum particles, exhibit wave-like properties. Erwin Schrodinger developed an equation to describe these waves, but the detection of quantum objects as particles presents a conundrum. Max Born proposed that the wave function should be interpreted as a probability, leading to the concept that quantum objects exist as a probability wave until measured, at which point the wave collapses to a particle. The speaker encourages viewers to stay tuned for a deeper understanding of these concepts.
📐 Quantum Mechanics' Challenges and Predictions
This paragraph delves into the challenges faced in quantum mechanics, particularly the measurement problem, which questions how the wave function collapses to a particle upon measurement. Despite this issue, quantum mechanics has been highly successful in predicting outcomes, leading some to adopt a philosophy of 'just shut up and calculate.' However, the speaker argues for the importance of seeking a deeper understanding of the universe, beyond just making predictions. The paragraph also touches on the wave-like nature of quantum objects, described by wave functions that are not localized and extend throughout space, leading to the Uncertainty Principle, which states that position and momentum of a quantum object cannot be known simultaneously due to the probabilistic nature of quantum mechanics.
🔬 Quantum Behavior in Macro Objects and the Nature of the Universe
The final paragraph addresses the question of why we don't observe wave behavior in macro objects like basketballs or dust particles. It explains that all objects, regardless of size, exhibit wave-like behavior, but the wavelengths for larger objects are so small compared to their physical size that their quantum properties are undetectable. The paragraph also discusses nonlocality and entanglement, phenomena that arise from the wave-like behavior of particles, and how these challenge our classical understanding of the universe. It corrects the common misconception of electrons in circular orbits around the nucleus, instead describing a probability cloud. The speaker emphasizes that the universe is quantized, with familiar quantities occurring in discrete units, and that Newtonian mechanics is an approximation of the quantum mechanical universe. The paragraph concludes with a plug for Brilliant.org, offering courses on quantum mechanics and a special offer for viewers.
Mindmap
Keywords
💡Quantum Mechanics
💡Wave-Particle Duality
💡Schrodinger Equation
💡Probability Wave
💡Measurement Problem
💡Uncertainty Principle
💡Entanglement
💡Quantization
💡Wavefunction
💡de Broglie Relation
Highlights
Quantum mechanics originated from the failure of classical mechanics to explain electron orbit in an atom without radiating energy.
Niels Bohr introduced quantized orbits to solve the problem of electron energy loss, linking orbits with Planck's constant.
Louis de Broglie proposed that if quantized orbits exist, electrons must be waves, which was later confirmed by experiments.
Erwin Schrodinger developed an equation to describe the wave-like behavior of quantum particles over time.
The wave-particle duality presents a conundrum as quantum objects are detected as particles, not waves.
Max Born suggested interpreting the wave function from Schrödinger's equation as a probability distribution.
Quantum objects do not have a distinct location but a probability of being found at any particular location, only determined upon measurement.
The 'measurement problem' in quantum mechanics questions how or why wave collapse occurs through measurement.
Despite the measurement problem, quantum mechanics allows for highly accurate predictions and measurements of outcomes.
Quantum mechanics is fundamentally different from classical mechanics, with objects exhibiting wave-like behavior instead of having distinct positions and velocities.
The Uncertainty Principle states that it's impossible to know both the exact position and momentum of a quantum object simultaneously.
Macroscopic objects also exhibit wave-like behavior, but their wavelengths are so small compared to their size that quantum properties are not noticeable.
Nonlocality in quantum mechanics leads to phenomena like 'entanglement', where particles exhibit strange correlations without instant communication.
The traditional model of electrons in circular orbits around an atom nucleus is incorrect; instead, they exist in a probability cloud.
The universe is quantized, with quantities like energy, momentum, and electric charge occurring in discrete units, not continuously.
Quantum mechanics is not limited to small scales; it underlies all of physics, with classical mechanics being an approximation of the quantum world.
Brilliant.org offers courses like 'Quantum objects' and 'Quantum mechanics with Sabine' to further understand the fundamentals of quantum science.
Brilliant's courses use hands-on simulations, interactive quizzes, and visual demonstrations for an engaging learning experience.
Arvin Ash viewers can get a special offer on Brilliant, including a 30-day free trial and a 20% discount for the first 200 subscribers.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: