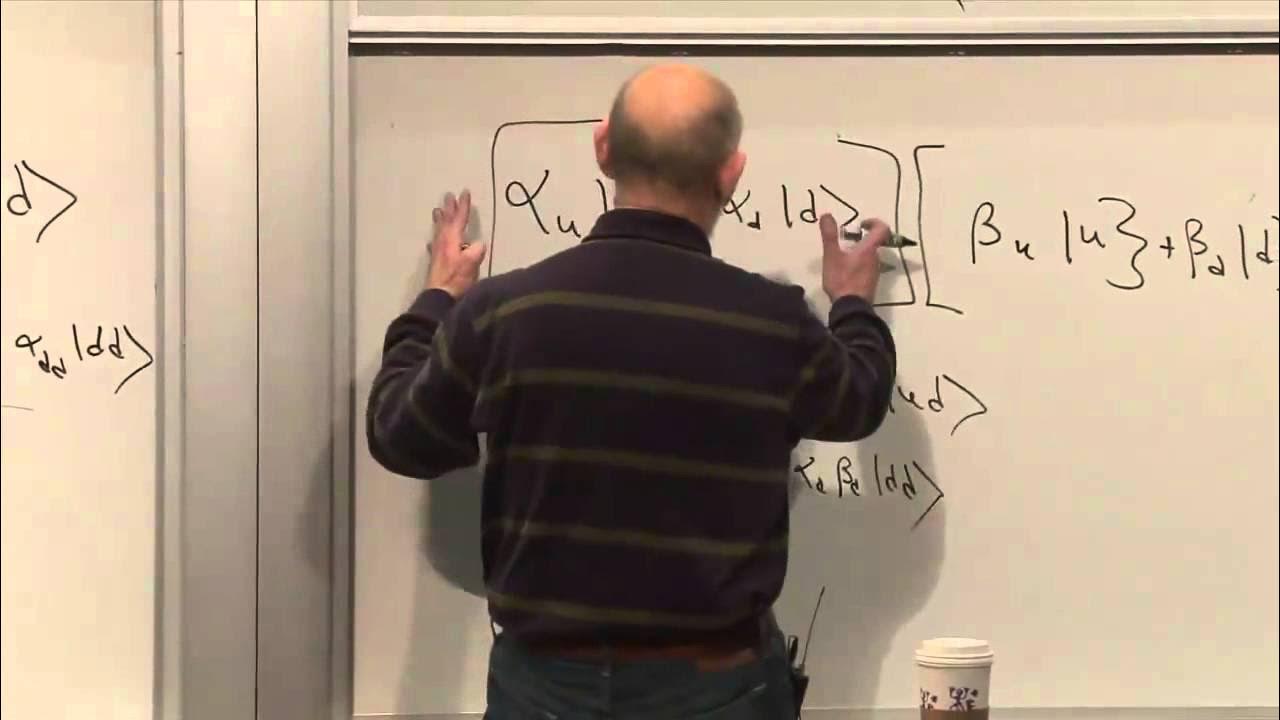Lecture 7 | Quantum Entanglements, Part 1 (Stanford)
TLDRThe video script delves into the intricacies of quantum mechanics, specifically focusing on the two-slit experiment and the concept of entanglement. It explains how the behavior of particles like electrons can be predicted using quantum superposition and interference patterns. The script explores the impact of measurement on these patterns, highlighting that observation or interaction with a system can lead to the collapse of the wave function and the loss of interference effects. The discussion extends to the role of entanglement in quantum systems, where the state of one particle can be intrinsically linked to another, regardless of distance. The lecturer also introduces the concept of entropy in quantum mechanics, contrasting it with classical entropy and explaining its relevance to the knowledge and uncertainty associated with quantum states. The script is an invitation to ponder the probabilistic nature of quantum physics and the profound implications of entanglement and measurement on our understanding of the physical world.
Takeaways
- 📚 The two-slit experiment is a fundamental demonstration of quantum mechanics, showing how particles like electrons can display wave-like interference patterns when not measured, but act like particles when observed or measured.
- 🚧 When a measurement is made to determine which slit a particle goes through, the interference pattern is destroyed, indicating the role of observation in quantum mechanics.
- ⚛️ The concept of superposition allows a quantum system to be in multiple states simultaneously, but this superposition collapses to a definite state upon measurement.
- 🧬 Entanglement is a quantum phenomenon where particles become linked, and the state of one instantly influences the state of another, regardless of the distance separating them.
- 🔍 The act of measurement in quantum mechanics is not just about obtaining information but involves a significant change in the state of the system being measured.
- 📉 The uncertainty principle implies that there is a limit to the precision with which certain pairs of physical properties of a particle, like position and momentum, can be known.
- 🌐 The wave function describes the quantum state of a system, and its square gives the probability distribution of finding a particle in a particular state.
- ⛓️ The collapse of the wave function is not a physical process but rather a way to describe the transition from a quantum system's probabilities to a definite outcome upon measurement.
- 🔢 Entropy in quantum mechanics is analogous to classical entropy and is a measure of the lack of knowledge about a system, with the quantum version involving the density matrix and its eigenvalues.
- 🤔 The concept of entanglement entropy will be further explored to understand the degree of entanglement between quantum systems and how it can be quantified.
- ⏯️ The process of entanglement and the resulting interference patterns are delicate and can be influenced by various factors, including the environment and the act of observation or measurement.
Q & A
What is the two-slit experiment?
-The two-slit experiment is a classic physics experiment that demonstrates the dual nature of light and other particles. It involves a source emitting particles (like electrons or photons) toward a barrier with two slits, and a screen behind the barrier where the particles arrive and create a pattern. The experiment shows interference patterns that suggest the particles behave like waves when not observed, but act like particles when measured.
How does the act of measurement affect the outcome of the two-slit experiment?
-Measurement in the two-slit experiment affects the outcome by collapsing the wave function. If one observes which slit the particle goes through, the interference pattern is destroyed because the act of measurement introduces an entanglement between the particle and the measuring device, eliminating the superposition of states.
What is entanglement in quantum mechanics?
-Entanglement is a quantum phenomenon where the quantum states of two or more particles become intertwined so that the state of one particle cannot be described independently of the state of the other particles. This leads to correlations between the particles that can persist even over large distances.
What is the role of the trace operation in quantum mechanics?
-The trace operation is used in quantum mechanics to calculate the sum of the diagonal elements of a matrix, which corresponds to the sum over states in classical probability. It is invariant under changes of basis and is used to find the average or expectation value of an observable in a quantum state.
What is the density matrix and how is it used in quantum mechanics?
-The density matrix is a mathematical tool used in quantum mechanics to describe a system when the preparation of the system is not perfectly known. It is a positive-semidefinite matrix with trace equal to one, representing a probability distribution over the system's state. It is used to calculate the average values of observables and to determine the entropy of a quantum system.
How is entropy defined in the context of a quantum system?
-In quantum mechanics, entropy is defined as the trace of the density matrix of a system multiplied by the logarithm of the density matrix. It quantifies the amount of uncertainty or lack of knowledge about the system's state. If the system is in a definite state, the entropy is zero, whereas for a mixed state with uncertainty, the entropy is greater than zero.
What is entanglement entropy and how does it relate to the entanglement of quantum systems?
-Entanglement entropy is a measure of the degree of entanglement between two quantum systems. It is defined as the entropy of the reduced density matrix of one subsystem when the combined system is in an entangled state. A non-zero entanglement entropy indicates that the two systems are entangled.
Why is the concept of a density matrix necessary when describing quantum systems?
-The concept of a density matrix is necessary when describing quantum systems because it allows for the representation of mixed states and statistical ensembles. It is used when there is uncertainty about the exact state of the system, and it encodes the probabilities of finding the system in different states upon measurement.
What is the significance of the trace of the product of an observable and the density matrix?
-The trace of the product of an observable and the density matrix gives the average or expectation value of that observable for the quantum system described by the density matrix. This is a generalization of the classical concept of averaging over a probability distribution and is essential for predicting the outcomes of quantum measurements.
How does the act of measurement in quantum mechanics lead to the collapse of the wave function?
-The act of measurement in quantum mechanics leads to the collapse of the wave function because the measurement process entangles the quantum system with the measuring apparatus. This entanglement causes the superposition of states to reduce to a single state, which is then observed, thus 'collapsing' the wave function to that particular state.
What is the difference between a pure state and a mixed state in quantum mechanics?
-A pure state in quantum mechanics is described by a single state vector or a coherent superposition of state vectors, representing a situation with complete knowledge of the system. A mixed state, on the other hand, is described by a density matrix and represents a statistical ensemble of possible states, reflecting a lack of complete knowledge about the system's exact state.
Outlines
🔬 Introduction to the Two-Slit Experiment
The paragraph introduces the two-slit experiment, a fundamental demonstration in quantum physics that explores the dual nature of light and matter. The speaker discusses the setup of the experiment, where an electron (or photon) is emitted from a source and passes through two slits, leading to an interference pattern on a screen. The concept of superposition and the evolution of states in a linear fashion are also explained, emphasizing the quantum nature of particles.
📐 Classical vs. Quantum Probabilities in the Two-Slit Experiment
This paragraph delves into the probabilities of an electron reaching the end point M when either slit A or B is open, and how these probabilities change when both slits are open. It contrasts classical probability theory, where probabilities are additive, with quantum mechanics, where interference effects lead to a more complex probability calculation. The interference term, unique to quantum mechanics, is highlighted as a key aspect of the experiment.
👀 Observing the Two-Slit Experiment: The Role of Measurement
The speaker explores what happens when an observer measures which slit the electron passes through, thus collapsing the wave function. By adding a spin degree of freedom to the system, the electron's path can be inferred without directly observing it, leading to the loss of interference pattern. The paragraph discusses the concept of entanglement and how the act of measurement affects the quantum system.
🚧 The Impact of Momentum and Energy on the Two-Slit Experiment
This paragraph discusses the effects of momentum and energy on the two-slit experiment. It explores the idea that the barrier through which the electron passes can have an energy gap, which may or may not be excited by the electron, thus affecting whether a mark is left behind. The uncertainty principle is also mentioned, explaining the spread in momentum space due to the localization of the barrier.
🧲 Formal Calculation of Probability in the Two-Slit Experiment
The paragraph outlines the formal process of calculating the probability of finding the electron at point M, considering both the spin-up and spin-down states. It explains the use of projection operators and the importance of orthogonality in quantum states, leading to the conclusion that the interference pattern is affected by the entanglement with the spin state.
🌟 The Role of Measurement in Quantum Mechanics
This paragraph emphasizes the role of measurement in quantum mechanics, explaining that the act of measurement can destroy interference patterns. It discusses the idea that if no record of which path the electron took is left behind, an interference pattern can emerge. Conversely, any record or mark that could indicate the path destroys the interference, a fundamental aspect of quantum mechanics.
🌌 Quantum Interference and the Many-Particle Scenario
The speaker discusses the concept of quantum interference in the context of many particles, like electrons or photons, and how it relates to wave functions. It is explained that the interference pattern emerges from the wave nature of these particles and that the presence of many particles does not change the fundamental principles observed with single particles.
🐱 Schrodinger's Cat and Entanglement
This paragraph uses the thought experiment of Schrodinger's cat to illustrate the concept of entanglement. It clarifies that the cat, when entangled with a system such as a gun, is not in a superposition of alive and dead states, but rather the composite system of the cat and the gun is in a superposition of states. The importance of the act of measurement in collapsing the wave function is also discussed.
📏 The Uncertainty Principle in Quantum Measurements
The paragraph touches on the uncertainty principle and how it plays a role in quantum measurements. It suggests that the uncertainty in the momentum of the screen in the two-slit experiment prevents the determination of the exact path of the electron, thus allowing for the interference pattern to form.
🤔 The Ambiguity in Defining a Measurement in Quantum Systems
The speaker ponders the ambiguity in defining where the act of measurement occurs within a quantum system. It is suggested that the process of measurement involves entanglement and that the point at which the wave function collapses can be ambiguous, depending on how one delineates the system and the observer.
🌱 Entropy and the Degree of Entanglement
This paragraph introduces the concept of entropy in the context of quantum mechanics, specifically in relation to entanglement. It explains that entropy can be used as a measure of the degree of entanglement between two systems and outlines the idea of entanglement entropy, which will be further discussed in subsequent parts of the lecture.
Mindmap
Keywords
💡Two-slit experiment
💡Quantum superposition
💡Entanglement
💡Wave function collapse
💡Interference pattern
💡Density matrix
💡Entanglement entropy
💡Observable
💡Trace
💡Hermitian operator
💡Probability distribution
Highlights
The two-slit experiment is revisited, emphasizing the role of quantum superposition and interference.
The concept of linear evolution of quantum states is introduced, explaining how states evolve without a preferred path.
The importance of entanglement in quantum mechanics is discussed, showing how measuring one particle can affect another.
The collapse of the wave function is explained, illustrating how observation leads to a definite outcome in quantum events.
The role of interference in the presence of an observer or recording device is explored, highlighting the transition from quantum to classical behavior.
The impact of the environment on quantum systems is discussed, noting how continuous measurement can prevent the spread of the wave function.
The uncertainty principle is applied to the two-slit experiment, explaining why it's impossible to determine the exact path of a quantum particle.
The idea of quantum entanglement is connected to the famous Schrödinger's cat thought experiment, emphasizing the superposition and entanglement of macroscopic states.
The concept of entanglement entropy is introduced as a measure of the degree of entanglement between two quantum systems.
The density matrix is explained as a tool for describing quantum states when there is uncertainty about the system's preparation.
The average value of an observable in quantum mechanics is derived using the density matrix and the trace operation.
The quantum mechanical entropy is defined and related to the classical concept, showing how it indicates the lack of knowledge about a system.
The relationship between entropy, information, and the maximum entropy of a system is clarified, with examples.
The program outlines the process for determining entanglement through entanglement entropy, which will be further explored with examples in future sessions.
The trace theorem is highlighted, noting that the trace of a matrix is invariant and does not depend on the choice of basis vectors.
The use of the density matrix to describe subsystems within an entangled composite system is explained, without needing to consider the entire system.
The program concludes with a预告 (preview) of future discussions on working out real examples of entanglement entropy.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: