20. Quantum Mechanics II
TLDRThe transcript is a detailed discussion on quantum mechanics, focusing on the double-slit experiment and the concept of wave-particle duality. The professor emphasizes the importance of asking questions and engaging with the material, highlighting that quantum mechanics operates on rules that differ from our everyday experiences. The wave function, its square giving the probability density of finding a particle, is a central theme. The lecture touches on the Heisenberg Uncertainty Principle, which dictates the inherent limits of precision in measuring the position and momentum of a particle simultaneously. The complexity of quantum mechanics is further illustrated through thought experiments, such as the behavior of electrons in the double-slit experiment, which challenge classical physics. The summary of the lecture aims to pique interest in the probabilistic nature of quantum mechanics and the fundamental questions it raises about the reality of particle locations and properties prior to measurement.
Takeaways
- 📚 The professor emphasizes the importance of asking questions throughout the learning process, as understanding quantum mechanics requires active engagement and discussion.
- 🌐 The concept of a 'reasonable world' is challenged in quantum mechanics, suggesting that the rules and calculations used in this field may not align with everyday experiences.
- 📉 The professor introduces the idea that quantum mechanics, specifically the double-slit experiment, contradicts Newtonian physics, indicating a fundamental shift in understanding the behavior of particles.
- 🚫 The professor stresses that the act of measuring or observing a quantum event can influence the outcome, which is a key principle in quantum mechanics known as the observer effect.
- 🤔 The uncertainty principle is highlighted, suggesting that it is impossible to simultaneously know the exact position and momentum of a particle, a concept that deviates from classical physics.
- 🚧 The script discusses the wave-particle duality, where particles like electrons exhibit both wave-like and particle-like properties, which is central to quantum mechanics.
- 📍 The probability density function, represented by the square of the wave function (Y^2), is used to determine the likelihood of finding a particle in a particular location.
- 🔄 The normalization of the wave function is crucial as it ensures the total probability of finding the particle anywhere in space sums up to 1.
- 🧮 The Gaussian function is introduced as an example of a wave function that describes the probability distribution of finding a particle and is normalized to represent a definite physical situation.
- ⚖️ The Heisenberg Uncertainty Principle is illustrated through the thought experiment of trying to measure the position and momentum of a particle, emphasizing the inherent limits in our knowledge at the quantum level.
- 🔑 The script touches on the potential applications of quantum mechanics, including the development of quantum computers, which could revolutionize data security and computational power.
Q & A
What is the key experiment that challenges Newtonian mechanics and introduces the quantum world?
-The key experiment that challenges Newtonian mechanics and introduces the quantum world is the double-slit experiment. It demonstrates the wave-particle duality of particles like electrons, which cannot be explained by classical physics.
How does the double-slit experiment show that particles like electrons do not follow a single trajectory?
-In the double-slit experiment, when both slits are open, the pattern of where electrons hit the screen does not correspond to the sum of the patterns when each slit is open individually. This indicates that the electrons do not have a single trajectory but rather behave like waves, interfering with themselves to create a pattern that cannot be explained by particle trajectories alone.
What is the relationship between the momentum of an electron and its wavelength in quantum mechanics?
-The relationship between the momentum (p) of an electron and its wavelength (λ) in quantum mechanics is given by the de Broglie equation: λ = h / p, where h is the Planck's constant.
Why is it difficult to simultaneously know the exact position and momentum of a particle in quantum mechanics?
-The difficulty in simultaneously knowing the exact position and momentum of a particle in quantum mechanics is due to the Heisenberg Uncertainty Principle, which states that the product of the uncertainties in position (Δx) and momentum (Δp) cannot be less than a certain minimum value, approximately equal to Planck's constant divided by 4π (Δx * Δp ≥ ħ/2).
What is the role of probability in quantum mechanics?
-In quantum mechanics, probability is used to describe the likelihood of finding a particle in a particular state or position. Unlike classical mechanics, where outcomes are deterministic given enough information, quantum mechanics inherently involves probabilities due to the wave-like nature of particles and the uncertainties in their properties.
What is the significance of the wave function in quantum mechanics?
-The wave function (Y) in quantum mechanics is a mathematical description that encodes the probability amplitude for a particle's position, momentum, and other properties. The square of the wave function's magnitude (|Y|^2) gives the probability density of finding the particle at a certain location or with a certain momentum.
Why do we normalize the wave function in quantum mechanics?
-We normalize the wave function in quantum mechanics to ensure that the total probability of finding the particle anywhere in space adds up to 1, which is a fundamental requirement in probability theory. Normalization is achieved by adjusting the wave function so that the integral of its square over all space equals 1.
What is the concept of superposition in quantum mechanics?
-Superposition in quantum mechanics is the concept where a particle can exist in multiple states or locations simultaneously, represented by the sum of its possible wave functions. It is a fundamental principle that allows for the existence of quantum states that are not found in classical physics.
How does the act of measurement affect the state of a quantum system?
-The act of measurement in quantum mechanics causes the wave function to collapse to a definite state. Before measurement, a quantum system exists in a superposition of states, but upon measurement, it assumes a specific value with a certain probability, as determined by the square of the wave function's amplitude.
What is the role of complex numbers in describing quantum states?
-Complex numbers are essential in quantum mechanics for describing the wave function of a particle, especially when dealing with states of definite momentum. The use of complex numbers allows for the representation of the phase of the wave function, which is crucial for understanding phenomena such as interference and the probabilistic nature of quantum mechanics.
Why is it challenging to build a quantum computer?
-Building a quantum computer is challenging because it requires maintaining quantum coherence and isolating the quantum bits (qbits) from any external environment that could cause decoherence. Additionally, the need to perform precise measurements without collapsing the superposition of states adds to the complexity of designing and operating a quantum computer.
Outlines
😀 Introduction to Quantum Mechanics and the Double Slit Experiment
The professor begins an informal discussion on quantum mechanics, emphasizing the importance of asking questions to understand the strange phenomena that don't follow the rules of daily life. He stresses that quantum mechanics, unlike classical physics, is not about making the world reasonable but about stating the rules and calculating outcomes. The professor summarizes the last lecture, explaining that everything is made of particles such as electrons, photons, protons, and neutrons. He delves into the double slit experiment, which highlights the quantum mystery and contradicts Newtonian physics, to illustrate the particle nature of electrons and the problems that arise when attempting to observe their behavior.
🔬 The Double Slit Experiment and Newtonian Physics
The paragraph discusses the double slit experiment with electrons, which leads to a contradiction with Newtonian physics. When one slit is blocked, electrons behave as particles. However, when both slits are open, an interference pattern emerges, indicating a wave-like behavior. This experiment demonstrates that electrons do not follow a single trajectory, contradicting the predictions of Newtonian mechanics. The professor illustrates this with the example of a machine gun firing bullets through two holes in a wall, where opening the second hole would intuitively double the number of bullets reaching the target, but with electrons, opening both slits can sometimes result in no electrons reaching certain areas, a phenomenon that would never occur with classical particles.
🌊 Wave-Particle Duality and the Need for a New Understanding
The professor explains that the observed patterns in the double slit experiment are reminiscent of wave interference, such as with water or sound waves. This leads to the concept that an electron is associated with a wave function, where the square of the wave function's amplitude gives the probability of finding the electron at a certain location. The wavelength associated with the electron is derived from its momentum, and the experiment shows that the wave function is essential for calculating the outcomes of quantum events. The professor also discusses the implications of a single electron being described by a wave, and how this wave function gives the odds of where the electron will land upon observation.
📐 Heisenberg's Uncertainty Principle and the Single Slit Experiment
The professor introduces Heisenberg's Uncertainty Principle, which arises from the wave nature of particles. When attempting to localize a particle's position by passing it through a very small slit, the wave function spreads out, leading to greater uncertainty in the particle's momentum. This is demonstrated through the single slit experiment, where the uncertainty in position (Dx) and momentum (Dp) are related by the equation Dx * Dp ≥ ħ/2. The professor calculates the uncertainty in the y-component of momentum (Dpy) for an electron passing through a slit and shows that it is related to the slit width (d) and the electron's wavelength (λ), emphasizing the inherent uncertainty in both position and momentum at the quantum level.
🔍 The Role of Probability in Quantum Mechanics
The professor discusses the probabilistic nature of quantum mechanics, contrasting it with the deterministic outcomes of classical mechanics. In quantum mechanics, the wave function provides the probability of finding a particle in a particular location, but it does not determine a single outcome. This is likened to statistical predictions in classical mechanics, such as the odds of a coin landing heads or tails, which in practice are determined by numerous trials. However, unlike classical mechanics, where the exact outcome is theoretically calculable but impractical to determine, quantum mechanics inherently involves probabilities due to the wave-particle duality and the act of measurement affecting the outcome.
🚫 The Limitations of Macroscopic Analogies in Quantum Mechanics
The professor emphasizes that while macroscopic analogies can sometimes help illustrate quantum mechanical concepts, they can also be misleading. Quantum mechanics deals with probabilities and the superposition of states, which have no direct analog in the macroscopic world. The act of measurement in quantum mechanics is crucial as it collapses the wave function and determines the particle's position. This is unlike macroscopic objects, which always have definite positions that are simply being observed. The professor warns against accepting any macroscopic analogy that suggests otherwise, as the quantum world is fundamentally different.
🤔 The Challenge of Building a Quantum Computer
The professor discusses the concept of a quantum bit or qbit, which unlike classical bits that are either 0 or 1, can exist in a superposition of states, representing both 0 and 1 simultaneously. This property allows quantum computers to perform many calculations at once, offering exponential speedup for certain problems like factorization. However, building a quantum computer is challenging because qbits must be isolated from the environment to maintain their quantum state, yet they must also be interacted with to perform calculations and read the results. The professor humorously suggests that the ability to build a quantum computer could lead to fame, tenure, or the ability to go on a significant shopping spree.
📊 Normalization of the Wave Function in Quantum Mechanics
The professor explains the concept of normalization in quantum mechanics, which is the process of scaling the wave function so that the integral of the probability density function over all space is equal to 1. This ensures that the total probability of finding the particle somewhere in space is 100%. The professor provides examples of how to normalize different types of wave functions, such as a rectangular wave function and a Gaussian wave function, and emphasizes the importance of this procedure for making accurate probabilistic predictions in quantum mechanics.
🧐 The Connection Between Wave Functions and Momentum
The professor prompts students to consider how information about momentum, a key quantity in classical mechanics, is contained within the wave function in quantum mechanics. While it might be tempting to think that a separate function is needed to describe momentum probabilities, the professor hints that the wave function Y(x) itself contains all the necessary information. This sets the stage for a deeper exploration of how various physical quantities, including momentum, energy, and others, can be derived from the wave function, which will be discussed in subsequent lectures.
Mindmap
Keywords
💡Quantum Mechanics
💡Wave-Particle Duality
💡Double-Slit Experiment
💡Uncertainty Principle
💡Wave Function
💡Normalization
💡Probability Density
💡Momentum
💡Superposition
💡Observer Effect
💡Quantum Coherence
Highlights
The professor emphasizes the importance of asking questions throughout the learning process to better understand complex subjects like quantum mechanics.
Quantum mechanics is introduced as a non-intuitive subject where strange phenomena occur, differing from daily life experiences.
The double-slit experiment is highlighted as key to understanding the quantum mystery and the limitations of Newtonian physics.
The professor explains that particles such as electrons behave like particles when detected but exhibit wave-like properties in the double-slit experiment.
The wave function, denoted by Y(x), is introduced as a mathematical function whose square gives the probability of finding a particle at a certain location.
The concept of wave-particle duality is discussed, where particles like electrons display both wave and particle characteristics.
The Heisenberg Uncertainty Principle is mentioned, which implies a fundamental limit to the precision with which certain pairs of physical properties can be known.
The professor uses the example of a machine gun and a wall with two holes to illustrate the counter-intuitive results of the double-slit experiment.
The idea that quantum mechanics provides probabilities rather than certainties is a central theme of the lecture.
The role of the observer in quantum mechanics is touched upon, where the act of measurement affects the outcome.
The professor discusses the mathematical representation of particles with definite momentum using complex exponentials, e^(i px/ℏ).
The concept of normalization of the wave function is explained as a necessary step to ensure the probabilities add up to 1.
The lecture touches on the potential of quantum computers and the challenges in building them due to the need for isolation from external interactions.
The professor suggests that macroscopic objects do not exhibit quantum effects due to the averaging out of quantum fluctuations.
The difference between classical and quantum probabilities is clarified, with the latter being inherent to the system rather than a lack of knowledge.
The superposition principle is discussed, where a quantum system can exist in multiple states simultaneously until measured.
The lecture concludes with a teaser about the upcoming topic of how to extract information about momentum and other observables from the wave function.
Transcripts
Browse More Related Video
19. Quantum Mechanics I: The key experiments and wave-particle duality
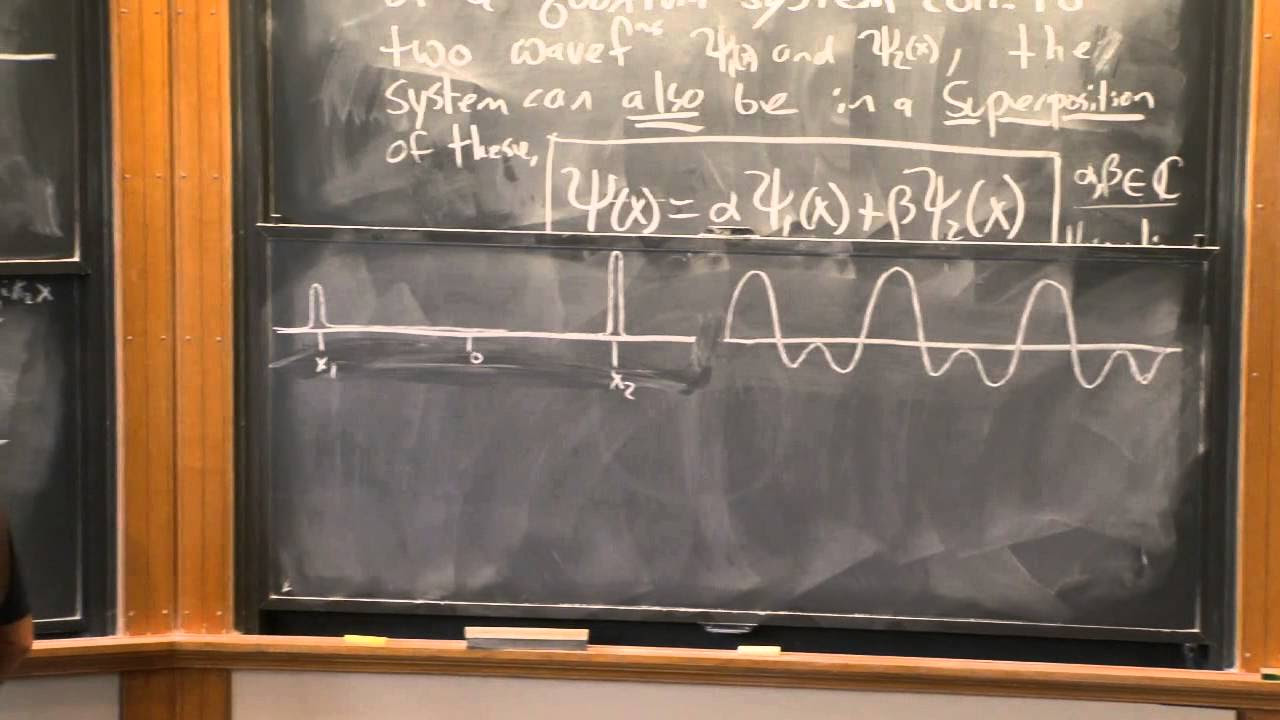
Lecture 3: The Wave Function
Lecture 2: Experimental Facts of Life

What Is Quantum Mechanics Explained

Can You Capture a Light Wave? Mind-Blowing Wave-Particle Duality Experiment!

22. Quantum mechanics IV: Measurement theory, states of definite energy
5.0 / 5 (0 votes)
Thanks for rating: