Electric Flux, Gauss's Law & Electric Fields, Through a Cube, Sphere, & Disk, Physics Problems
TLDRThis video script delves into the concept of electric flux, explaining its calculation and relation to electric fields and surfaces. It covers scenarios where the electric field is perpendicular and parallel to the surface, using examples like a sphere with enclosed charges and a cube with a central charge. The script employs Gauss's law to simplify complex calculations and demonstrates how the sign of the electric flux (positive or negative) depends on the direction of the electric field relative to the surface normals.
Takeaways
- 🌟 Electric flux is a measure of the total electric field lines passing through a surface.
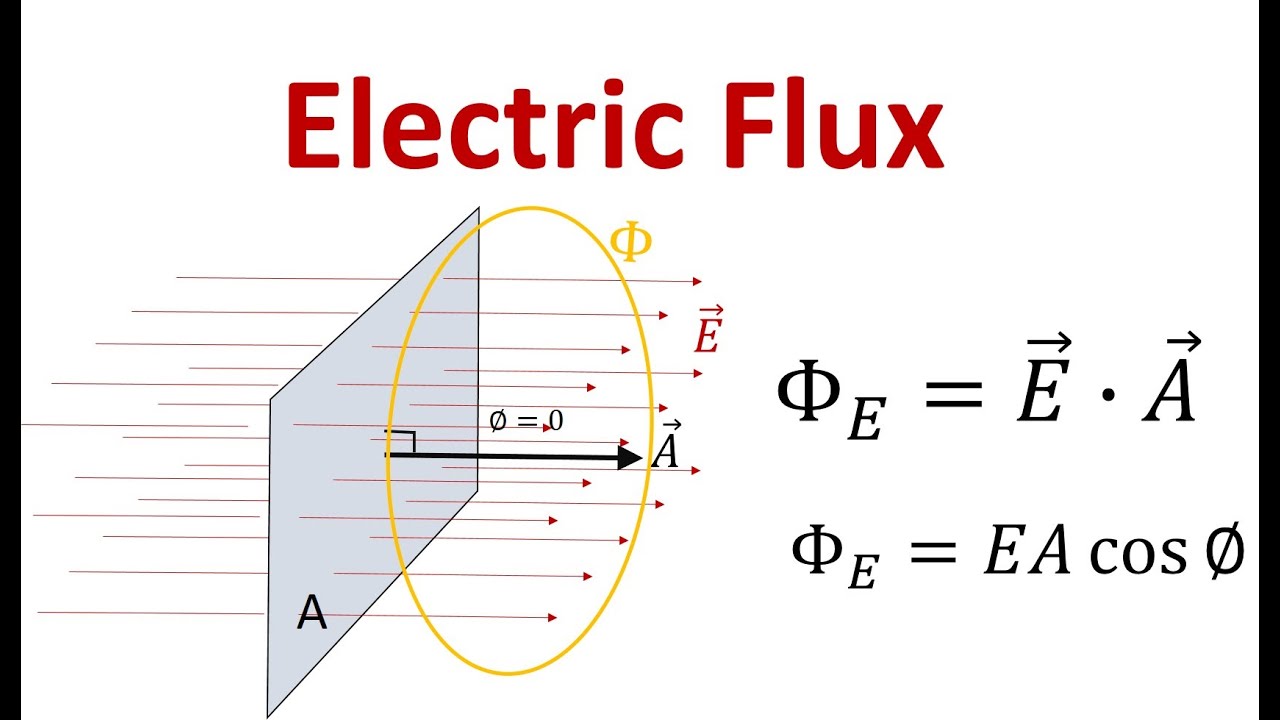
- 📐 The formula for electric flux (Φ) is the product of the electric field (E), area (A), and the cosine of the angle (phi) between the field and the normal to the surface (cos φ).
- 🔄 When the electric field is perpendicular to the surface, the angle phi is 0, and cos 0 is 1, resulting in the maximum flux (E*A).
- 🔄 If the electric field is parallel to the surface, the angle phi is 90 degrees, and cos 90 is 0, leading to zero electric flux through the surface.
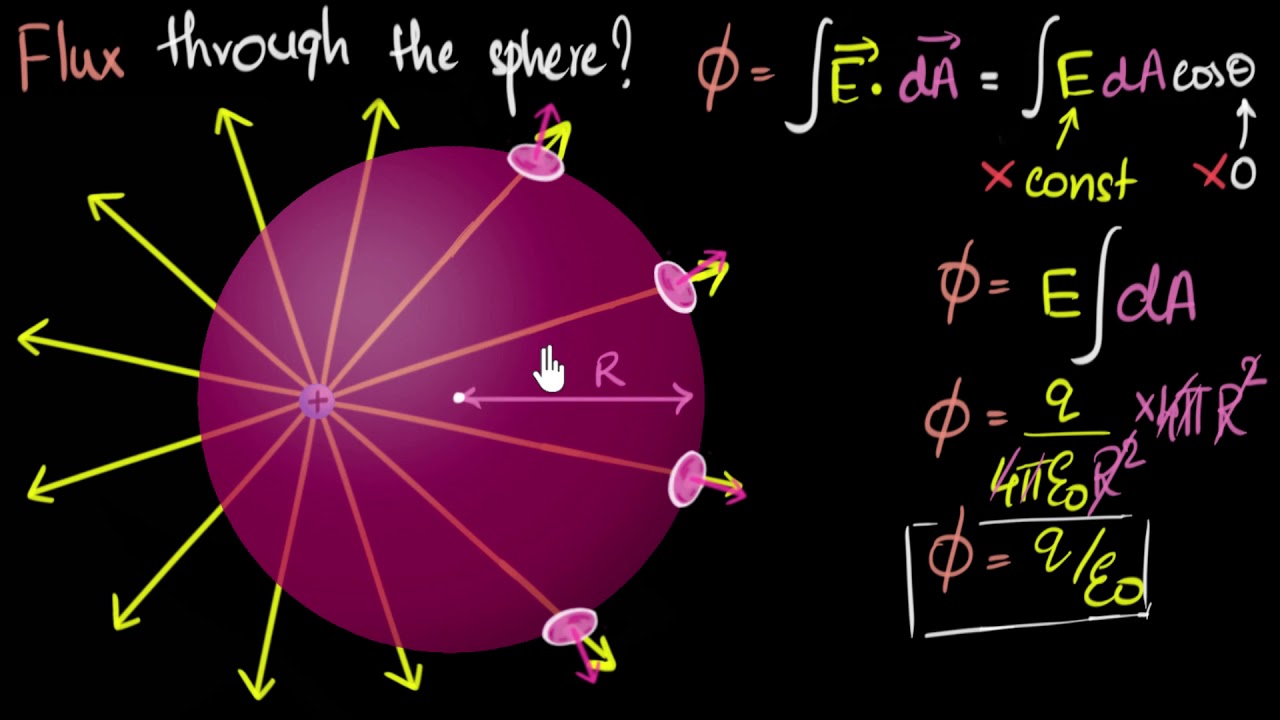
- 🌐 For a sphere with a charge, the electric field is always perpendicular to the surface, and the flux can be calculated as the charge enclosed divided by the vacuum permittivity (ε₀).
- 🔢 The electric flux through a sphere with a positive charge is positive (outward flux), and with a negative charge, it is negative (inward flux).
- 📊 For a horizontal disk with an electric field at an angle, the flux is calculated as the product of the electric field (E), the area (A), and the cosine of the angle (cos φ).
- 🎯 Gauss's law simplifies the calculation of electric flux by stating that it is proportional to the charge enclosed by the surface (Q/ε₀).
- 🔎 For a cube with a charge at the center, the total electric flux outside the cube is the charge enclosed divided by ε₀, which is positive.
- 🔍 If calculating the flux through one face of the cube, divide the total flux by the number of faces (in this case, 6).
- 🚫 For a cube with no charge and an external electric field, the net electric flux through a closed surface is zero, as the entering and leaving fluxes cancel each other out.
Q & A
What is electric flux?
-Electric flux is a measure of the total electric field that passes through a given surface. It is calculated as the product of the electric field and the area of the surface, with the electric field being perpendicular to the surface.
How is electric flux calculated when the electric field is perpendicular to the surface?
-When the electric field is perpendicular to the surface, the electric flux is simply the product of the electric field strength and the surface area. This is because the angle between the electric field and the normal to the surface is 0 degrees, and cosine 0 degrees is 1.
What happens to the electric flux if the electric field is not perpendicular to the surface?
-If the electric field is not perpendicular to the surface, the electric flux is calculated as the product of the electric field strength, the surface area, and the cosine of the angle between the electric field and the normal to the surface.
What is the maximum value of electric flux?
-The maximum value of electric flux occurs when the electric field is perpendicular to the surface, making the angle between them 0 degrees. In this case, the cosine of the angle is 1, leading to the maximum product of the electric field and the surface area.
How is electric flux related to the charge enclosed by a sphere?
-The electric flux through a sphere is proportional to the charge enclosed by the sphere. According to Gauss's law, the electric flux is equal to the charge enclosed divided by the permittivity of free space (epsilon sub naught).
What is the electric flux through a sphere with a radius of 4 meters containing a 50 micro coulomb charge?
-The electric flux through such a sphere is positive and can be calculated using the formula: (charge enclosed / epsilon sub naught). For a 50 micro coulomb charge, the flux is 5.65 times 10 to the 6th power newtons times square meters per coulomb.
How does the sign (positive or negative) of the charge enclosed by a sphere affect the electric flux?
-A positive charge inside a sphere results in an outward electric flux, which is positive. Conversely, a negative charge results in an inward electric flux, which is negative. The magnitude of the flux is the same in both cases, but the sign depends on the charge's polarity.
What is the electric flux through a horizontal disk with a radius of 3 meters and an electric field at an angle of 30 degrees?
-The electric flux through the disk is calculated as the product of the electric field strength, the area of the disk (pi times r squared), and the cosine of the angle (60 degrees in this case). With an electric field of 100 newtons per coulomb, the flux is 450 pi newtons times square meters per coulomb.
How can Gauss's law be used to calculate the total electric flux emanating outside of a cube with a positive charge at its center?
-Gauss's law states that the total electric flux is equal to the charge enclosed divided by the permittivity of free space. For a cube with a 30 micro coulomb charge, the total electric flux is 3.39 times 10 to the 6th power newtons times square meters per coulomb, which is positive.
What is the electric flux through one face of the cube if the total electric flux through the cube is known?
-To find the electric flux through one face of the cube, divide the total electric flux by the number of faces. For a cube, this would be one-sixth of the total flux.
What is the net electric flux through a cube with no charge inside when an electric field passes through it perpendicular to its faces?
-The net electric flux through such a cube is zero. This is because the electric flux entering through one face (bottom) is equal in magnitude and opposite in sign to the flux leaving through the other face (top), leading to a cancellation effect.
Outlines
🌟 Introduction to Electric Flux
This paragraph introduces the concept of electric flux, explaining it as the product of the electric field and the area of a surface perpendicular to the field. It discusses how the angle between the electric field and the normal to the surface affects the electric flux, with the maximum flux occurring when the angle is zero. The paragraph then presents a problem involving a sphere with charges and calculates the electric flux through the sphere using the surface area and the electric field produced by the enclosed charges. The explanation emphasizes Gauss's law, which relates electric flux to the enclosed charge.
📉 Electric Flux with Charges Inside a Sphere
This paragraph continues the discussion on electric flux, focusing on how the nature of the charge inside a sphere affects the flux. It explains that with a positive charge, the electric field is directed outward, resulting in a positive flux, while a negative charge results in an inward electric field and a negative flux. The example provided contrasts the magnitude of flux for both positive and negative charges inside a sphere. The paragraph then moves on to discuss a horizontal disk with an electric field at an angle, showing how to calculate the flux through the disk using the electric field, the area, and the cosine of the angle between the field and the disk's normal.
🔲 Calculating Electric Flux for Various Geometries
This paragraph explores the calculation of electric flux for different geometric shapes, such as a cube with a central charge and a cube without any charge. It emphasizes the use of Gauss's law as a convenient method for calculating the total electric flux through closed surfaces, as it is proportional to the enclosed charge. The example with the cube demonstrates how to calculate the flux through each face when there is a charge inside and how the fluxes through opposite faces cancel each other out when there is no charge present, resulting in a net flux of zero, consistent with Gauss's law.
Mindmap
Keywords
💡Electric Flux
💡Electric Field
💡Gauss's Law
💡Charge
💡Surface Area
💡Perpendicular
💡Cosine
💡Angle
💡Positive and Negative Charges
💡Closed Surface
💡Epsilon Sub Naught
Highlights
Electric flux is defined as the product of the electric field and the perpendicular area of a surface.
The electric field times the area is equal to the electric flux, with phi being the angle between the normal line and the electric field.
When the electric field is perpendicular to the surface, the angle phi is zero, and cosine zero is one, resulting in maximum electric flux.
If the electric field is not perpendicular to the surface, the electric flux is calculated as the electric field times the area times the cosine of phi.
For a sphere with a charge at its center, the electric field is always perpendicular to the surface, leading to a straightforward calculation of electric flux.
The electric flux through a sphere with a positive charge is an outward flux and is positive, while with a negative charge, it is an inward flux and is negative.
The electric flux through a horizontal disk can be calculated by considering the electric field, the area of the disk, and the cosine of the angle between the electric field and the plane of the disk.
Gauss's law states that the electric flux is proportional to the charge enclosed by the object, simplifying the calculation of electric flux in complex scenarios.
For a cube with a charge at its center, the total electric flux emanating outside of the cube can be calculated using Gauss's law, which is equal to the charge enclosed divided by epsilon sub naught.
When calculating the electric flux through one face of a cube, the total electric flux is divided by the number of faces (in this case, six).
In a cube with no charge, the electric flux through the top and bottom faces can be determined by considering the direction of the electric field relative to the surfaces.
The net electric flux through a closed object with no charge is zero, as the flux that enters is equal to the flux that leaves, according to Gauss's law.
The concept of electric flux is crucial in understanding the behavior of electric fields and their interaction with various surfaces and objects.
The angle between the electric field and the normal to the surface plays a significant role in determining the magnitude of the electric flux.
The electric flux is a fundamental concept in electromagnetism and has practical applications in the design and analysis of electrical systems.
The use of trigonometry, specifically cosine, is essential in calculating electric flux when the electric field is not perpendicular to the surface.
The electric flux is a vector quantity, and its direction is determined by the direction of the electric field relative to the surface.
The concept of electric flux is particularly useful in electrostatics, where it helps in determining the distribution of charges and electric fields.
Understanding electric flux allows for the efficient calculation of electric fields in complex geometries, such as spheres, disks, and cubes.
The electric flux is zero for surfaces where the electric field is parallel to the plane of the surface, as the cosine of 90 degrees is zero.
The calculation of electric flux through different shapes illustrates the versatility of electromagnetic principles in solving real-world problems.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: