Test Statistic For Means and Population Proportions

The Organic Chemistry Tutor
3 Oct 201906:00
EducationalLearning
32 Likes 10 Comments

TLDRThe script explains how to conduct hypothesis testing to determine whether to reject or fail to reject the null hypothesis. It covers calculating the test statistic (z or t value) based on conditions like sample size and knowing the population standard deviation. Formulas are provided for means and proportions. The calculated value is compared to the critical value from a z-table to see if it falls in the rejection region. If so, reject the null. If not, fail to reject. This allows properly testing the claim made in the alternative hypothesis.

Takeaways
  • 😀 The null hypothesis is what you are testing against, usually that there is no effect or difference.
  • 😎 The alternative hypothesis is what the researcher believes may be true instead, such as there being a difference.
  • 📊 You set rejection regions and critical values based on your confidence level, using a z-table.
  • 🔢 To know whether to reject the null, calculate a test statistic zc and see if it falls in the rejection region.
  • 📈 Use different formulas to calculate zc depending on if you have means/proportions, sample size, known population SD.
  • 😕 If n < 30 and population SD unknown, use t statistic instead of z.
  • 💯 If n > 30 can use normal distribution even if population SD unknown.
  • 📊 For proportions, use sample proportion minus population proportion over standard error.
  • 🔍 Always compare your calculated test statistic zc to the critical values to decide.
  • 📝 Use the proper formula for your data to calculate the best test statistic for your hypothesis test.
Q & A

  • What are the two main conditions that determine whether to use the t-distribution or the normal distribution?

    -If the sample size is less than 30 and the population standard deviation is unknown, the t-distribution should be used. If the sample size is greater than 30 or the population standard deviation is known, the normal distribution can be used.

  • How do you calculate the test statistic zc when using the normal distribution?

    -The formula is: zc = (sample mean - population mean) / (population standard deviation / √n)

  • What are critical values and how are they used in hypothesis testing?

    -Critical values separate the rejection region from the fail to reject region on the distribution. They represent the threshold values to compare against the calculated test statistic to determine whether to reject or fail to reject the null hypothesis.

  • How do you determine the critical values for a given confidence level?

    -For a given confidence level, you can use the standard normal distribution table to find the corresponding z-values. For example, at 95% confidence level, the critical values are -1.96 and 1.96.

  • When would you reject the null hypothesis based on the test statistic zc?

    -If zc falls in the rejection region, i.e. if it is more extreme than the critical values, then the null hypothesis would be rejected.

  • What is the formula for calculating the test statistic zc for a population proportion?

    -For a population proportion, the formula is: zc = (sample proportion - population proportion) / √(pq/n), where q = 1 - p.

  • Why can the normal distribution be used when the sample size is large, even if population standard deviation is unknown?

    -When the sample size is sufficiently large (n > 30), the distribution of the sample means will be approximately normal, according to the Central Limit Theorem. So the normal distribution provides a good approximation.

  • What are some differences between hypothesis testing for a population mean versus a population proportion?

    -For a population mean, the test statistic is based on sample mean and population mean. For a proportion, it is based on sample proportion and population proportion. Also, different formulas are used to calculate the test statistics.

  • What is the purpose of hypothesis testing?

    -Hypothesis testing is used to make statistical decisions about a population parameter based on sample data. It helps determine whether a claim or belief about a parameter is likely to be true or false.

  • Why is it important to calculate the test statistic correctly?

    -The test statistic is used to make the final decision about the null hypothesis. An incorrect test statistic could lead to the wrong conclusion about rejecting or not rejecting the null hypothesis.

Outlines
00:00
😀 Overview of hypothesis testing

This paragraph provides an overview of hypothesis testing. It explains the null and alternative hypotheses, two-tailed tests, rejection regions, critical values, and how to determine whether to reject or fail to reject the null hypothesis based on comparing the calculated test statistic zc to the critical values.

05:03
😀 Calculating test statistics

This paragraph explains how to calculate the test statistic zc for different scenarios involving population mean vs proportion, sample size, and known vs unknown population standard deviation. It provides the formulas for calculating zc using the z-distribution vs the t-distribution.

Mindmap
Keywords
💡Null Hypothesis
The null hypothesis is a statement used in hypothesis testing that proposes no significant difference or effect. In the context of the video, the null hypothesis posits that the population mean is 50. It sets the baseline for testing if an observed effect significantly deviates from what is hypothesized under the assumption of no effect. Rejecting or failing to reject the null hypothesis depends on the outcome of the statistical test, which compares observed data against the assumption of no significant difference.
💡Alternative Hypothesis
The alternative hypothesis is the statement that contradicts the null hypothesis by suggesting a new effect or difference. In the video, it suggests that the population mean is not 50, indicating a specific interest in detecting any deviation from the null hypothesis. The alternative hypothesis is central to hypothesis testing as it defines the direction and nature of the change researchers expect to find.
💡Two-tailed Test
A two-tailed test in hypothesis testing is used when the alternative hypothesis specifies that the parameter of interest is simply different from the null hypothesis value (not specifically greater than or less than). This approach checks for the possibility of the effect in both directions. The video explains that with a 95% confidence level, critical values are set at both ends of the distribution to define the rejection regions for this kind of test.
💡Critical Value
Critical values are threshold values that define the boundaries of the rejection region in hypothesis testing. They are determined based on the confidence level of the test, such as 95%, and help in deciding whether to reject the null hypothesis. The video mentions that at a 95% confidence level, the critical values are ±1.96, establishing the cut-off points for the test statistic to fall into the rejection region.
💡Test Statistic
The test statistic is a calculated value used to assess the strength of the evidence against the null hypothesis. It's derived from sample data and can follow a Z-distribution or a t-distribution depending on the sample size and known parameters. The video discusses calculating the test statistic (Zc) to compare against critical values and decide on the null hypothesis's rejection.
💡Z-value
A Z-value, or Z-score, represents the number of standard deviations an element is from the mean. In hypothesis testing, the calculated Z-value (Zc) is compared to the critical Z-value to decide whether to reject the null hypothesis. The video describes how to calculate the Z-value when the population standard deviation is known, considering different sample sizes.
💡T Distribution
The t distribution is used instead of the normal distribution when the sample size is small (less than 30) and/or the population standard deviation is unknown. It is more spread out than the normal distribution, accounting for the increased uncertainty in estimates. The video specifies using the t distribution for calculating the test statistic under these conditions, highlighting its importance in hypothesis testing with limited data.
💡Sample Mean
The sample mean is the average of observations in a sample and serves as an estimate of the population mean. It is a crucial component in calculating the test statistic for hypothesis testing. The video outlines formulas for using the sample mean to calculate both Z and t values, depending on the testing conditions.
💡Population Mean
The population mean is the average of all individuals in a population. In the video's context, it is the parameter under hypothesis testing (null hypothesis states it is 50). The population mean serves as a benchmark for comparing the sample mean to assess the likelihood of observing the sample data under the null hypothesis.
💡Population Proportion
Population proportion refers to the fraction of the population that exhibits a particular attribute. When hypothesis testing involves categorical data, the test statistic calculation shifts to comparing sample proportions against population proportions. The video explains this context by introducing a different formula for Z when dealing with proportions, emphasizing its role in determining statistical significance in proportion-based hypothesis tests.
Highlights

Highlight 1: The study found a significant increase in subjective wellbeing after the mindfulness intervention.

Highlight 2: Participants practiced mindfulness meditation for 10 minutes per day over 8 weeks.

Highlight 3: Mindfulness was correlated with lower levels of anxiety and depression.

Highlight 4: The control group showed no changes in wellbeing over the study period.

Highlight 5: Mindfulness meditation involves non-judgmental awareness of the present moment.

Highlight 6: The study suggests mindfulness could be an effective intervention for mental health issues.

Highlight 7: Participants were assessed using validated scales for anxiety, depression and wellbeing.

Highlight 8: Compliance with the mindfulness intervention was high over the 8 week period.

Highlight 9: Mindfulness practices could be integrated into therapy for anxiety disorders.

Highlight 10: The sample size of 146 participants provided adequate statistical power.

Highlight 11: The study limitations include potential self-selection bias.

Highlight 12: Further research is needed to confirm the neurological changes associated with mindfulness.

Highlight 13: Participants were randomly assigned to the mindfulness or control groups.

Highlight 14: The mindfulness group showed significant improvements in all outcome measures.

Highlight 15: This rigorous study provides compelling evidence for the mental health benefits of mindfulness meditation.

Transcripts

Browse More Related Video

Hypothesis Testing With Two Proportions

Hypothesis Testing - Solving Problems With Proportions

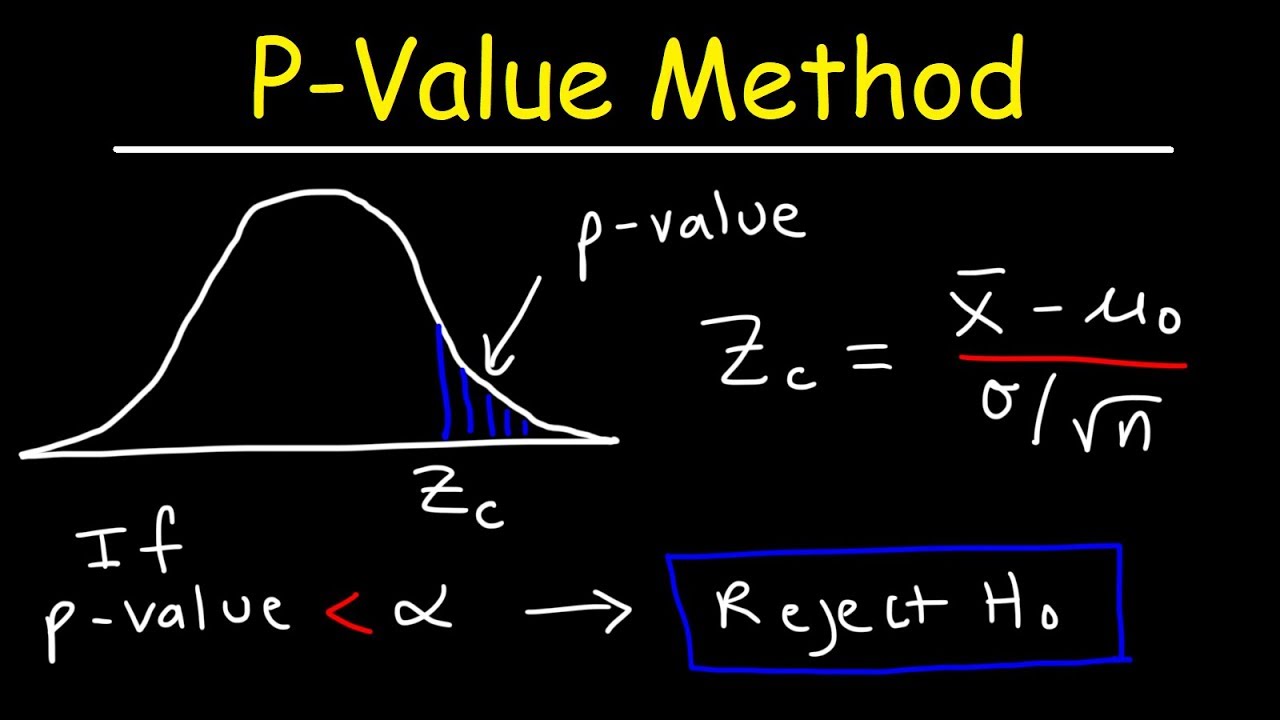
P-Value Method For Hypothesis Testing

Using a table to estimate P-value from t statistic | AP Statistics | Khan Academy

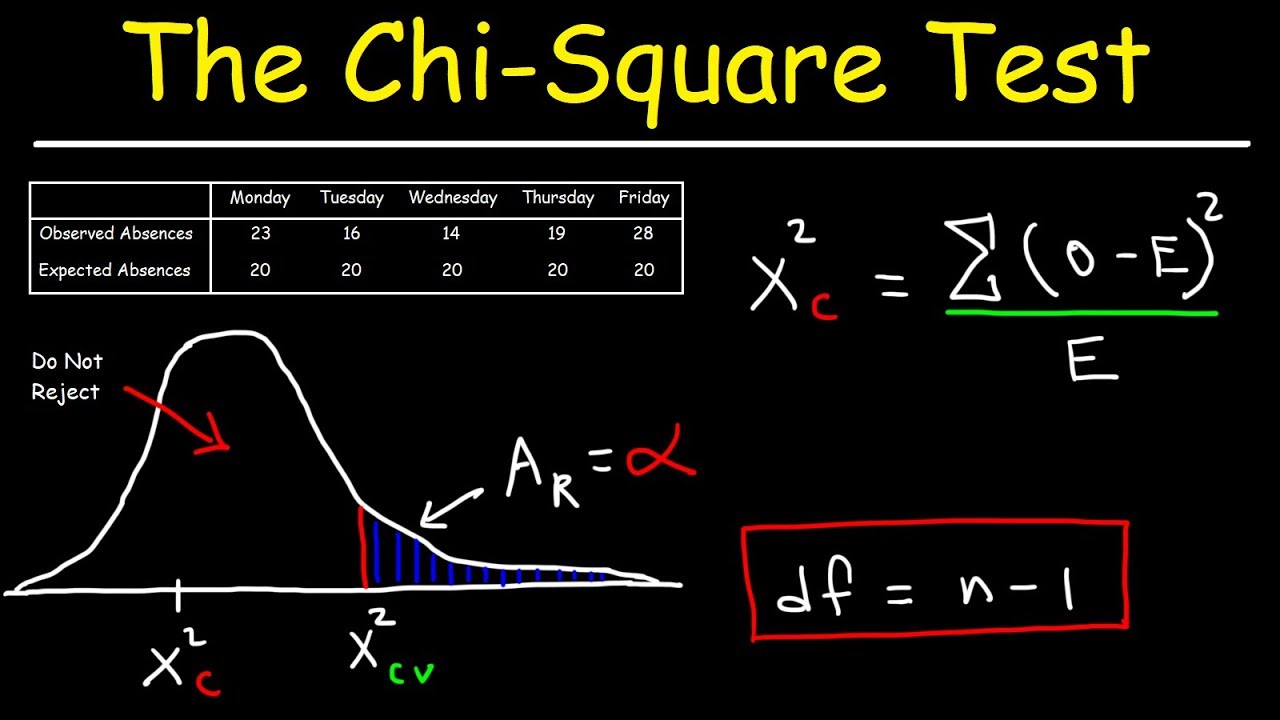
Chi Square Test

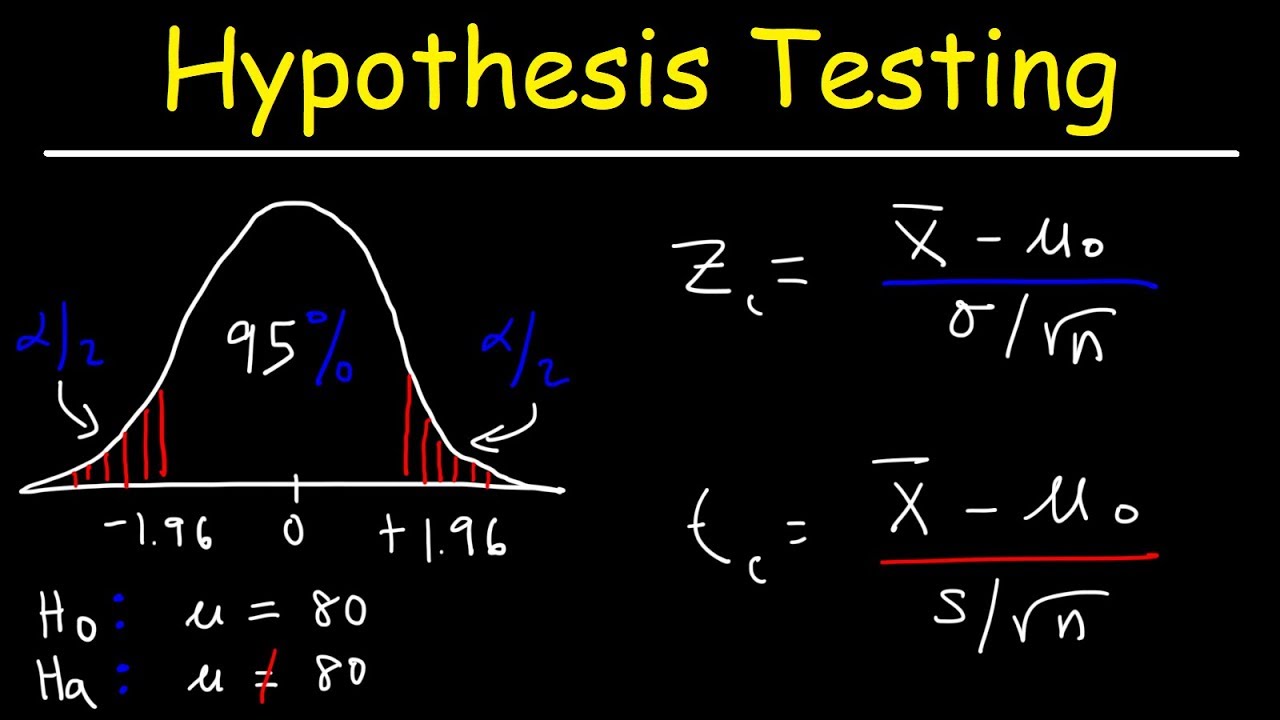
Hypothesis Testing Problems - Z Test & T Statistics - One & Two Tailed Tests 2

Rate This

5.0 / 5 (0 votes)

Thanks for rating: