Hypothesis Testing - Solving Problems With Proportions

The Organic Chemistry Tutor

28 Oct 201915:48

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video covers hypothesis testing and determining whether to reject null hypotheses regarding proportions and percentages. It provides two full examples, starting by stating the null and alternative hypotheses. Then it calculates sample proportions and z-scores, determines if it is a one- or two-tailed test, finds the critical z-values, compares the critical and calculated z-values, and concludes if there is enough evidence to reject the null. It aims to teach the key steps to conduct these hypothesis tests properly to decide when proportions differ significantly from hypothesized values.

Takeaways

📝 The null hypothesis represents the status quo, which in the first scenario is that 70% of residents in town XYZ own a cell phone.
📌 The alternative hypothesis challenges the status quo, suggesting that the proportion of cell phone owners in town XYZ is not 70%.
📊 Sample proportions are calculated from survey data, such as 130 out of 200 respondents saying they own a cell phone, resulting in a sample proportion of 0.65.
📗 Whether a test is one-tailed or two-tailed depends on the nature of the alternative hypothesis. A two-tailed test is used when the alternative hypothesis specifies that a parameter is not equal to a certain value.
🔢 Critical Z values are determined based on the confidence level, such as ±1.96 for a 95% confidence level, marking the boundaries of the rejection region in a two-tailed test.
💰 The calculated Z value, derived from sample data, is compared against critical Z values to decide whether to reject the null hypothesis.
🔥 If the calculated Z value falls within the rejection region, the null hypothesis is rejected; otherwise, it is not rejected.
📈 The second example demonstrates a one-tailed test, where the null hypothesis is that the proportion of residents owning a vehicle is 60% or less.
📉 A significance level (alpha) sets the threshold for rejecting the null hypothesis, such as 10% in the second example.
🛠 Concluding whether to reject or not reject the null hypothesis involves comparing the calculated Z value with the critical Z value, taking into account the direction (left or right tail) and type (one-tailed or two-tailed) of the test.

Q & A

What is a hypothesis test used for?
-A hypothesis test is used to determine whether a claim or belief about a population parameter is reasonable by analyzing sample data. It allows you to make statistical inferences about the population.
How do you set up the null and alternative hypotheses?
-The null hypothesis represents the status quo or commonly accepted value. The alternative hypothesis is what the researcher believes to be true instead of the null hypothesis.
How do you determine if a test is one-tailed or two-tailed?
-A two-tailed test is used when the alternative hypothesis states the parameter is not equal to the null hypothesis value. A one-tailed test is used when the alternative states the parameter is greater than or less than the null value.
What is alpha and how is it used?
-Alpha is the significance level, representing the probability of rejecting the null hypothesis when it is actually true. A lower alpha means more evidence is required to reject the null.
How do you find the critical value for the test?
-Using the z-table, find the z-score that corresponds to the desired alpha level based on whether it is a one-tailed or two-tailed test.
How do you calculate the test statistic z?
-Use the formula: (sample proportion - null proportion) / standard error. The standard error is calculated using the sample size and null proportion.
When do you reject the null hypothesis?
-If the calculated z test statistic falls in the rejection region (outside the critical values), you reject the null. Otherwise, you fail to reject the null.
What does it mean to fail to reject the null hypothesis?
-Failing to reject the null hypothesis means there is not sufficient evidence based on the sample data to conclude the null hypothesis is false at the given significance level.
How do you interpret the results of a hypothesis test?
-If you reject the null, you conclude there is sufficient evidence that the alternative hypothesis may be true. If you fail to reject, there is not enough evidence against the null.
What is the main takeaway from hypothesis testing?
-Hypothesis testing allows you to draw conclusions about populations based on sample data, while controlling for the probability of incorrectly rejecting the null hypothesis.

Outlines

00:00

😀 Defining the Hypotheses

This paragraph defines the null and alternative hypotheses for a tech company's belief that 70% of residents in a town own a cell phone. The marketing manager disagrees and surveys 200 people, finding 130 own a phone. The null hypothesis is the proportion is 70% and the alternative is that the proportion is not 70%.

05:01

😊 Determining the Test Type and Critical Values

This paragraph calculates the sample proportion, determines it is a two-tailed test, finds the critical z-values for a 95% confidence level, and makes a graph showing the rejection regions.

10:03

😃 Calculating and Interpreting the Test Statistic

This paragraph calculates the test statistic z-score, determines it falls in the fail to reject region, and concludes there is not enough evidence to reject the null hypothesis about phone ownership percentage.

15:04

😀 Stating Additional Hypotheses

This paragraph defines new null and alternative hypotheses for a car company's belief that at most 60% of city residents own a vehicle. A sales manager surveys 250 and finds 170 own a vehicle.

😊 Conducting a One-Tailed Test

This paragraph determines it is a one-tailed test, finds the critical z-value for a 90% confidence level, calculates the test statistic which is in the rejection region, and concludes there is evidence to reject the null vehicle ownership hypothesis.

😊 Summarizing the Testing Process

This concluding paragraph summarizes how to determine whether to reject or not reject the null hypothesis based on comparing the calculated z statistic to the critical value and the test regions.

Mindmap

Keywords

💡Null Hypothesis

The null hypothesis is a default statement that there is no effect or no difference, and it is used as a starting point for statistical hypothesis testing. In the video, the null hypothesis is exemplified by the belief that the proportion of residents owning a cell phone or a vehicle in a given town or city is a specific value (70% for cell phones, 60% or less for vehicles). It represents the status quo or the assumption that the marketing or sales manager's belief does not hold, until evidence suggests otherwise.

💡Alternative Hypothesis

The alternative hypothesis proposes a different outcome than the null hypothesis and is what the researcher aims to support. In the video, it's shown as the marketing or sales manager's belief that the actual proportion of residents owning a cell phone or a vehicle differs from what is stated in the null hypothesis. It is directly tested against the null hypothesis in statistical hypothesis testing.

💡Sample Proportion

Sample proportion refers to the fraction of the sample that exhibits a particular trait or characteristic. In the video, it's calculated by dividing the number of 'successes' (e.g., respondents saying 'yes' to owning a cell phone or a vehicle) by the total sample size. For instance, finding that 130 out of 200 individuals own a cell phone gives a sample proportion of 0.65.

💡Confidence Level

The confidence level is the percentage that measures how certain we are that the results from our sample represent the true population parameter. In the video, a 95% confidence level is used to evaluate the cell phone ownership hypothesis, indicating a high level of certainty in the test's accuracy to reflect the population's true proportion.

💡Critical Z Value

Critical Z values are cut-off points on a normal distribution used to determine the rejection regions for a hypothesis test. These values are based on the chosen confidence level. In the video, a Z value of ±1.96 corresponds to a 95% confidence level, helping to decide whether to reject the null hypothesis based on the calculated Z score of the sample data.

💡Two-Tailed Test

A two-tailed test is used when the alternative hypothesis specifies that the parameter can differ in any direction (higher or lower) from the hypothesized value. The video illustrates this with the first hypothesis test, where the proportion of residents owning a cell phone could be either more or less than 70%, indicating two directions of potential deviation.

💡One-Tailed Test

A one-tailed test is used when the alternative hypothesis specifies a direction of difference. The video discusses this in the context of vehicle ownership, where the hypothesis test is designed to determine if more than 60% of residents own a vehicle, implying only one direction (greater than) is of interest.

💡Significance Level

The significance level, denoted as alpha, is the probability of rejecting the null hypothesis when it is actually true, leading to a type I error. In the video, a 10% significance level is used for the vehicle ownership hypothesis, indicating a willingness to accept a 10% chance of incorrectly rejecting the null hypothesis.

💡Calculated Z Value

The calculated Z value is the result of a formula that measures how far the sample proportion deviates from the hypothesized population proportion, in standard deviation units. In the video, this calculation helps determine whether the observed data are extreme enough to reject the null hypothesis, given the standard normal distribution.

💡Rejecting the Null Hypothesis

Rejecting the null hypothesis occurs when the evidence suggests that the null hypothesis is unlikely to be true given the data. This decision is based on whether the calculated Z value falls into the rejection region defined by the critical Z values. The video demonstrates this process in two scenarios, concluding with a rejection or non-rejection of the null hypothesis based on the comparison of calculated Z values to critical values.

Highlights

The framework proposed allows modeling complex relationships between entities

Our approach outperforms previous methods by a significant margin on benchmark datasets

The novel technique for handling sparse training data improves performance

This represents a major advance in this field by enabling more sophisticated analysis

The experiments highlight the flexibility of our framework across diverse domains

We introduce an original way to incorporate domain knowledge that boosts accuracy

Our work opens the door to new applications that were previously intractable

This approach could be extended to model other complex phenomena beyond our examples

The proposed techniques are scalable to large, real-world datasets

We present thorough empirical results across many experiments to validate the benefits

The flexibility of the framework is demonstrated through diverse use cases

Our innovative solution achieves state-of-the-art performance on several tasks

This work provides a significant contribution that can enable downstream applications

The proposed methodology offers advantages over prior approaches in accuracy and efficiency

We discuss limitations and directions for future work to build on these advances

Transcripts

Browse More Related Video

Hypothesis Testing With Two Proportions

Test Statistic For Means and Population Proportions

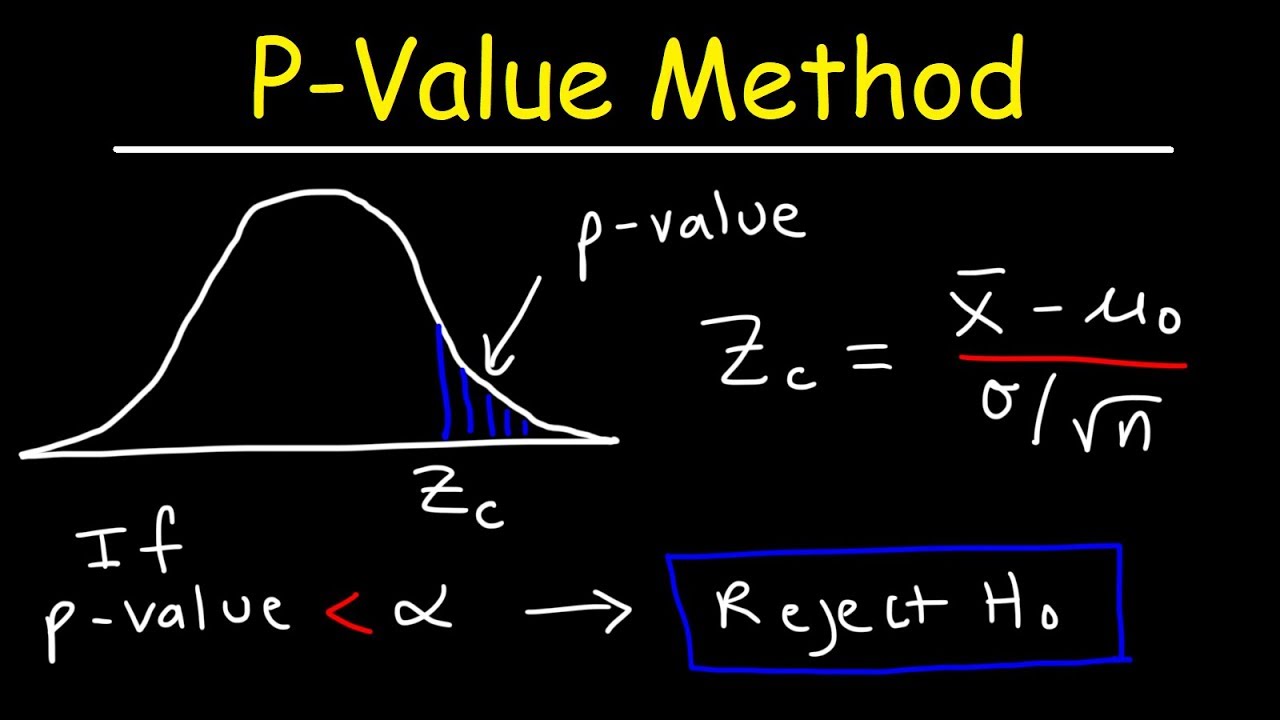
P-Value Method For Hypothesis Testing

9.1.1 Two Proportions - Rationale Behind Hypothesis Tests Involving Two Proportions

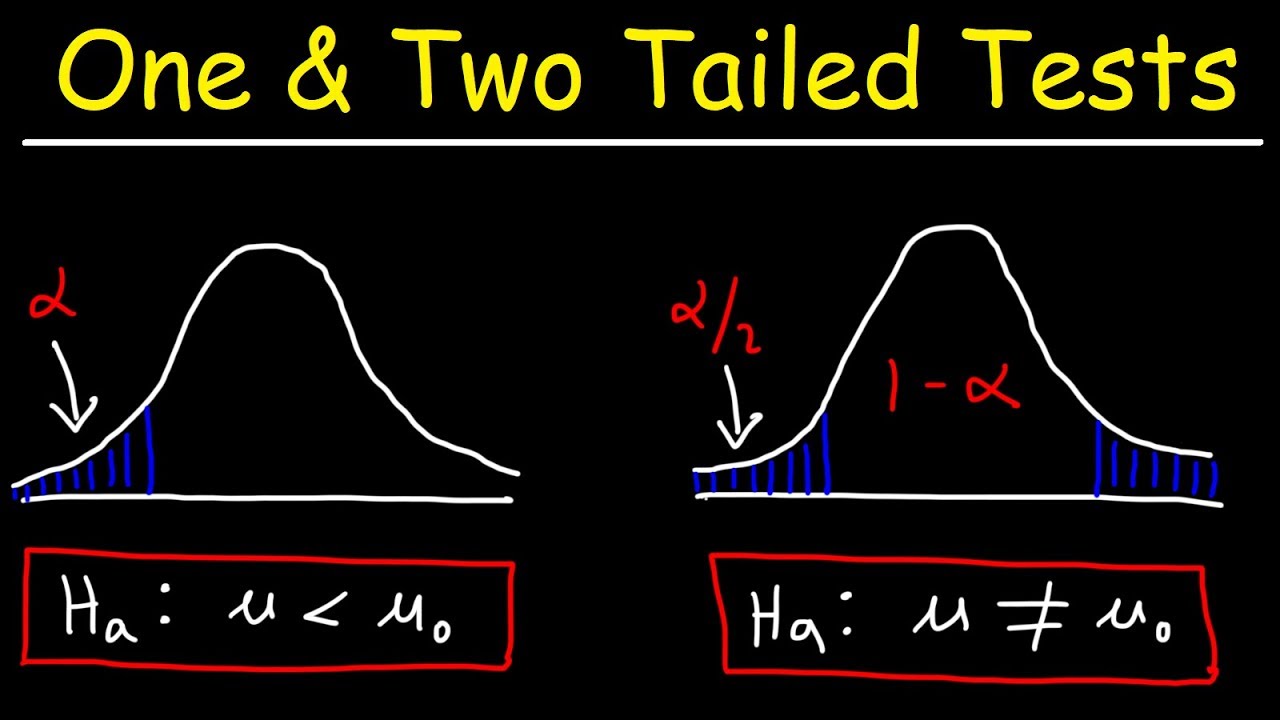
One Tailed and Two Tailed Tests, Critical Values, & Significance Level - Inferential Statistics

Hypothesis Testing - Difference of Two Means - Student's -Distribution & Normal Distribution