The Electric Flux and It's Applications

SirSACE PHYSICS

19 Feb 202026:56

EducationalLearning

32 Likes 10 Comments

TLDRThis video discusses electric flux and its applications. Electric flux is the measure of the electric field passing through a given area. It depends on the charge, electric field, and the area through which the field lines pass. The video explains the concept with examples, including the flux through a cube with charges inside and varying the orientation of a plane in a uniform electric field. It covers the mathematical formula for flux in both uniform and non-uniform fields and demonstrates problem-solving techniques for calculating flux through flat and curved surfaces.

Takeaways

😀 Electric flux is a measure of the electric field passing through a given area and is proportional to the number of field lines passing through a normally perpendicular surface.
🔍 The presence of an electric field does not guarantee flux; a surface area is required for flux to exist.
📏 Flux is a scalar quantity, meaning it only has magnitude without direction, and can be positive, negative, or zero depending on the orientation of the electric field relative to the surface.
⚙️ To calculate electric flux through a flat surface, use the formula involving the electric field (E), the area (A), and the cosine of the angle (θ) between the field and the normal to the surface.
📐 For a uniform electric field, the electric flux through an area is maximized when the angle between the field and the normal to the area is zero degrees, resulting in the maximum value of cosine (1).
📉 When the angle between the electric field and the normal to the area increases beyond 0 degrees up to 90 degrees, the flux decreases, becoming zero at 90 degrees where the field is perpendicular to the area.
📈 If the angle exceeds 90 degrees up to 180 degrees, the flux becomes negative because the cosine of the angle is negative, indicating the normal is in the opposite direction to the field.
🌐 For non-uniform electric fields or curved surfaces, the concept of flux is generalized using integral calculus to sum the contributions from infinitesimal areas over the entire surface.
🔢 The electric flux through a spherical surface due to a point charge is calculated by integrating the dot product of the electric field and infinitesimal area vector over the entire sphere, resulting in the total charge divided by the permittivity of free space.
📚 Understanding the principles of electric flux is essential for solving problems involving electric fields, especially when considering different orientations and shapes of surfaces in relation to the field.
🚀 The script emphasizes the importance of knowing the conditions for flux calculation, including the necessity of a surface area, the impact of the angle between the field and the normal, and the use of calculus for non-uniform or curved surfaces.

Q & A

What is electric flux?
-Electric flux is the measure of the electric field through a given area. It is proportional to the number of electric field lines passing through a normally perpendicular surface.
Does electric flux exist without an area?
-No, electric flux depends on the area. Without an area, there is no flux because flux is the measure of the electric field through a given area.
What happens to the electric flux if the charge within a box increases?
-If the charge within a box increases, the electric flux increases because more electric fields are produced, which means more electric flux.
Is electric flux a scalar or vector quantity?
-Electric flux is a scalar quantity, meaning it has magnitude but no direction.
What are the conditions for maximum electric flux?
-Maximum electric flux occurs when the angle between the electric field vector and the normal to the surface area is zero degrees, resulting in a cosine of 1.
How is the electric flux calculated for a flat surface and a uniform electric field?
-For a flat surface and a uniform electric field, the electric flux is calculated as the product of the magnitude of the electric field, the area of the surface, and the cosine of the angle between the electric field vector and the normal to the surface area.
What happens to the electric flux if the angle between the electric field and the area vector is 90 degrees?
-If the angle between the electric field and the area vector is 90 degrees, the electric flux is zero because the cosine of 90 degrees is zero.
What is the general formula for electric flux from a uniform electric field?
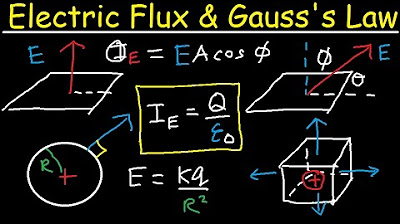
-The general formula for electric flux from a uniform electric field is Φ = E * A * cos(θ), where E is the electric field, A is the area, and θ is the angle between the electric field and the normal to the area.
How is electric flux calculated for a non-uniform electric field?
-For a non-uniform electric field, the electric flux is calculated using the integral of the electric field dot product with the infinitesimal area vector over the entire surface.
What is the value of the permittivity of vacuum (ε₀)?
-The permittivity of vacuum (ε₀) is 8.854 x 10^-12 Coulomb squared per Newton meter squared.
How does the orientation of the surface affect the electric flux?
-The orientation of the surface affects the electric flux by changing the angle between the electric field and the normal to the surface. As this angle changes, the cosine of the angle changes, thus altering the flux. When the angle is 0 degrees, the flux is maximum, and when it is 90 degrees, the flux is zero.

Outlines

00:00

🔋 Understanding Electric Flux and Its Applications

This paragraph introduces the concept of electric flux, which is the measure of electric field lines passing through a given area. It explains that electric flux is proportional to the number of electric field lines and the area perpendicular to these lines. The discussion uses the analogy of a church in Pacifica to illustrate the absence of flux without an area. The paragraph further explores the relationship between charge, electric fields, and flux, emphasizing the scalar nature of flux and its dependency on the electric field's magnitude and the area it penetrates. It concludes with the idea that increasing the charge results in a greater electric field and, consequently, a higher electric flux.

05:03

📚 Calculating Electric Flux with the Dot Product

The second paragraph delves into the mathematical representation of electric flux, using the dot product of the electric field and the area vector. It clarifies that the electric flux is maximized when the electric field is perpendicular to the area, resulting in a cosine of 0 degree, which equals 1. The paragraph discusses the implications of changing the orientation of the area relative to the electric field, demonstrating how the flux varies with the angle between them. It also addresses the scenario of a non-uniform electric field, where integration is used to calculate the total electric flux through an infinitesimal area element.

10:05

🌐 Exploring Electric Flux in Different Scenarios

This paragraph examines various situations affecting electric flux, such as when the area is beyond 90 degrees relative to the electric field, resulting in negative flux values. It also discusses the flux through a uniform electric field and how it is calculated using the formula E * A * cos(θ), where E is the electric field, A is the area, and θ is the angle between them. The paragraph provides an example of calculating electric flux through a ring in a uniform electric field, emphasizing the importance of the angle and the orientation of the area in determining the flux.

15:06

📘 Electric Flux in Curved Surfaces and Spherical Applications

The fourth paragraph extends the discussion to curved surfaces, specifically focusing on a spherical surface. It explains the process of calculating electric flux through an infinitesimal area on a sphere due to a point charge at its center. The paragraph uses integration to sum up the contributions from all infinitesimal areas on the sphere's surface, leading to the total electric flux. It also touches on the special case where the angle between the electric field and the area is zero, simplifying the calculation.

20:07

🔍 Detailed Calculation of Electric Flux from a Point Charge

This paragraph provides a detailed calculation of electric flux due to a point charge enclosed by an imaginary sphere. It uses the formula for the electric field of a point charge and integrates over the entire surface area of the sphere. The calculation demonstrates how the electric flux is related to the charge, the permittivity of free space, and the radius of the sphere, ultimately showing that the total electric flux through a spherical surface is independent of the sphere's size.

25:10

📝 Summary of Electric Flux Calculations and Principles

The final paragraph summarizes the principles and applications of electric flux calculations. It reiterates the importance of the area and the angle between the electric field and the area vector in determining the flux. The paragraph also highlights the use of calculus for calculating flux through curved surfaces and encourages solving problems to reinforce the understanding of electric flux concepts.

Mindmap

Keywords

💡Electric Flux

Electric flux is a scalar quantity that measures the total electric field passing through a given area, perpendicular to the direction of the field. It is central to the video's theme as it is the main concept being discussed. For instance, the script mentions that 'this electric flux is proportional to the number of field lines going through a normally perpendicular surface.'

💡Electric Field

An electric field is a vector field surrounding electrically charged particles, which exerts a force on other charged particles within the field. In the context of the video, the electric field is essential for calculating electric flux, as it is the field that passes through an area to produce flux. The script uses the term when explaining that 'flux depends on the area it is the mission or electric field through a given area.'

💡Perpendicular Surface

A perpendicular surface is a surface that is at a right angle (90 degrees) to the direction of the electric field. The script emphasizes the importance of this orientation for calculating electric flux, stating that 'flux is proportional to the number of field lines going through a normally perpendicular surface.'

💡Scalar Quantity

A scalar quantity is a physical quantity that can be described by a single numerical value, without direction. The script clarifies that 'flux is a scalar quantity which means that it has magnitude but there is no direction,' highlighting that electric flux, despite being influenced by the direction of the electric field, is a scalar because it does not have a direction associated with it.

💡Charge

In the context of the video, charge refers to the property of matter that gives rise to an electric field. The script relates charge to electric flux by stating that 'if we have more charges, we have more electric fields,' and thus, more electric flux, as flux is proportional to the number of electric field lines passing through an area.

💡Non-Uniform Electric Field

A non-uniform electric field is an electric field where the field strength varies from point to point. The script discusses how to calculate electric flux in such fields by considering an infinitesimal area and integrating over the entire surface, as opposed to a uniform field where a simple multiplication of field strength, area, and cosine of the angle can be used.

💡Dot Product

The dot product is a mathematical operation that takes two vectors and returns a scalar. In the script, the dot product is used to calculate electric flux, as it involves multiplying the electric field vector by the area vector and considering the cosine of the angle between them, as mentioned in 'the electric flux... is simply us by definition the electric field... the dot product of the electric field and the area vector.'

💡Cosine of the Angle

The cosine of the angle is a trigonometric function that relates the angle between two vectors to their dot product. The script explains that the magnitude of the electric flux is calculated by the product of the electric field's magnitude, the area's magnitude, and the cosine of the angle between them, as seen in 'the flux can be calculated by the product of the magnitude of electric field multiplied by the magnitude of the area normal to the surface area and multiplying by the cosine of the angle.'

💡Integration

Integration is a mathematical concept that allows for the calculation of areas, volumes, and other quantities by summing infinitesimal contributions. The script mentions integration in the context of calculating electric flux through a curved surface, where the flux is found by integrating the dot product of the electric field and the infinitesimal area vector over the entire surface, as described in 'so therefore this must be an infinity symbol electric flux so we have to integrate both sides.'

💡Permittivity

Permittivity is a property of a material that determines how it responds to an electric field, quantified as the amount of charge needed to create a unit electric field. The script refers to permittivity in the context of calculating the electric field of a point charge, which is given by '1 over 4 pi permittivity,' and is essential for understanding how electric fields interact with different media.

Highlights

Electric flux is a measure of the electric field through a given area and is proportional to the number of electric field lines passing through a perpendicular surface.

If there's no area, there's no electric flux because flux depends on the area through which the electric field lines pass.

Electric flux is a scalar quantity, meaning it has magnitude but no direction.

The formula for electric flux through a flat surface with a uniform electric field is the dot product of the electric field and the area vector.

The angle between the electric field and the normal to the surface determines the amount of electric flux.

Maximum flux occurs when the angle between the electric field and the normal to the surface is zero degrees.

If the area is perpendicular to the electric field, the flux is zero because the cosine of 90 degrees is zero.

Negative flux occurs when the angle between the electric field and the normal to the surface is between 90 and 180 degrees.

For non-uniform electric fields, the electric flux is calculated using integration over the surface.

The general formula for electric flux in a uniform electric field is given by E * A * cos(θ), where E is the electric field, A is the area, and θ is the angle between E and the normal to the area.

In the case of a curved surface, the electric flux is calculated by integrating the electric field over the infinitesimal areas of the surface.

The electric field of a point charge is given by E = 1/(4πε₀) * Q/r², where Q is the charge and r is the distance from the charge.

The flux through a spherical surface enclosing a charge is given by Q/ε₀, where ε₀ is the permittivity of free space.

Flux through a surface is maximum when the surface is oriented such that the electric field is perpendicular to the surface.

Calculating flux for non-uniform electric fields requires considering infinitesimal areas and integrating over the entire surface.

Transcripts

Browse More Related Video

Electric Flux

Electric Flux (part 1)

Electric Flux

Electric flux meaning (& how to calculate it) | Electrostatics | Physics | Khan Academy

Electric Flux, Gauss's Law & Electric Fields, Through a Cube, Sphere, & Disk, Physics Problems

Electric Flux and Gauss' Law - Review for AP Physics C: Electricity and Magnetism

Related Tags

Electric Flux Physics Electromagnetism Calculus Gauss's Law Surface Area Charge Distribution Field Lines Perpendicular Surface Dot Product