Electric Flux and Gauss’s Law | Electronics Basics #6

How To Mechatronics

1 Oct 201813:12

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video from howtomechatronics.com delves into the concept of electric flux and Gauss's law. It explains electric flux as the rate of electric field flow through a surface, using examples of both open and closed surfaces to illustrate how flux can be positive, negative, or zero. The video further demonstrates the relationship between electric flux and Gauss's law, showing how the total electric flux through a closed surface equals the enclosed charge divided by the permittivity of free space, epsilon naught. It also covers the application of Gauss's law in scenarios with spherical, cylindrical, and planar symmetry, providing equations for calculating electric fields in each case.

Takeaways

🌟 Electric flux is the rate of flow of electric field through a surface, which can be either open or closed.
📐 The differential of electric flux, \( d\phi \), through a small area element is defined as the dot product of the electric field magnitude \( E \) and the area vector \( d\vec{a} \), considering the angle \( \theta \) between them.
🔍 The total electric flux through a surface is calculated as the integral of \( d\phi \) over the entire area, resulting in a scalar quantity that can be positive or negative.
🔄 The unit of electric flux is newton meters squared per coulomb, indicating the amount of electric field penetrating a surface.
📊 The flux through different oriented surfaces in an electric field varies based on the angle between the field and the surface normal.
🌐 Gauss's law relates the electric flux through a closed surface to the total charge enclosed, divided by the permittivity of free space, \( \epsilon_0 \).
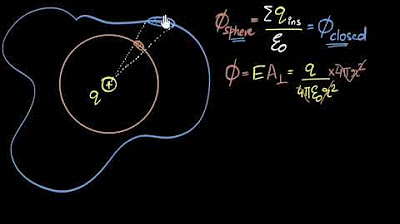
🔋 The total flux through a closed surface is independent of the distance from a point charge, as long as the charge distribution is uniform.
📏 Symmetry in charge distribution is crucial for calculating electric fields using Gauss's law, with three common types of symmetry: spherical, cylindrical, and planar.
🔬 For spherical symmetry, the electric field inside and outside a uniformly charged sphere can be determined using concentric spheres as Gaussian surfaces.
📐 In cylindrical symmetry, the electric field due to a line charge can be calculated using a cylinder as a Gaussian surface, considering the charge enclosed and the geometry of the cylinder.
🏗 For planar symmetry, the electric field around an infinite charged plane can be determined using a cylinder intersecting the plane as a Gaussian surface, leading to a constant electric field perpendicular to the plane.

Q & A

What is electric flux?
-Electric flux is the rate of flow of electric field through a given surface, representing the amount of electric field penetrating a surface, which can be either open or closed.
How is the differential of electric flux, dΦ, defined?
-The differential of electric flux, dΦ, is defined as the dot product of the magnitude of the electric field (E) and the magnitude of the vector area (dA), multiplied by the cosine of the angle (θ) between these two vectors.
What is the unit of electric flux?
-The unit of electric flux is newton meters squared per coulomb (Nm²/C).
How does the orientation of a surface affect the electric flux through it?
-The orientation of a surface affects the electric flux through it because the angle θ between the electric field vector and the area vector influences the dot product in the flux equation, thus changing the amount of flux.
What is the significance of the normal to a closed surface in calculating electric flux?
-The normal to a closed surface, by convention, points from the inside to the outside of the surface. It is used to determine the direction of the electric field relative to the surface when calculating the total flux through the closed surface.
How is Gauss's Law related to electric flux?
-Gauss's Law states that the electric flux through a closed surface is equal to the sum of all charges enclosed by the surface, divided by the permittivity of free space (ε₀). It is a direct relationship between the total flux and the enclosed charge.
What are the three types of symmetry that simplify the calculation of electric fields using Gauss's Law?
-The three types of symmetry that simplify the calculation of electric fields using Gauss's Law are spherical, cylindrical, and planar symmetry.
How does the electric field inside a hollow sphere with a uniformly distributed charge vary with distance from the center?
-The electric field inside a hollow sphere with a uniformly distributed charge is zero up to the radius of the sphere, and then it reaches its maximum value and decreases as the distance from the center increases.
What is the formula for the electric field around an infinite line of charge with uniform linear charge density (λ)?
-The electric field (E) around an infinite line of charge with uniform linear charge density (λ) is given by E = λ / (2πrε₀), where r is the distance from the line of charge and ε₀ is the permittivity of free space.
How does the electric field behave in the vicinity of a flat, infinite, large, horizontal plate with a uniform charge density (σ)?
-The electric field in the vicinity of a flat, infinite, large, horizontal plate with a uniform charge density (σ) has a constant value of σ / (2ε₀), and it does not depend on the distance from the plane.
What is the electric field between two infinitely large parallel plates with equal and opposite surface charge densities?
-The electric field between two infinitely large parallel plates with equal and opposite surface charge densities is constant and equal to the absolute value of the surface charge density divided by ε₀, pointing from the positively charged plate to the negatively charged plate.

Outlines

00:00

🔋 Understanding Electric Flux and Gauss's Law

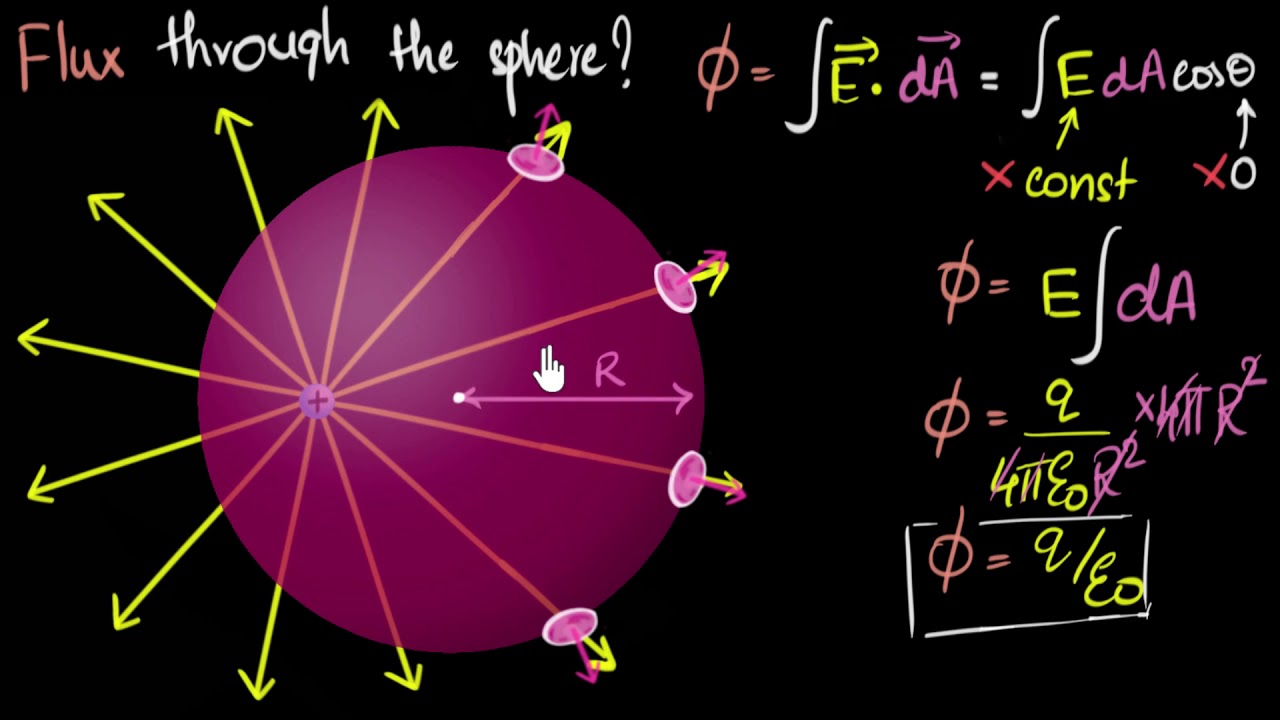
This paragraph introduces the concept of electric flux, which is the rate at which the electric field flows through a surface, whether it is open or closed. The explanation includes an example of an open surface with a uniform electric field and how to calculate the differential flux through small elements of the surface. The total flux is determined by integrating the differential flux over the entire surface. The paragraph also discusses the significance of the angle between the electric field and the surface normal, and how it affects the flux. The unit of electric flux is defined as newton meters squared per coulomb. The concept is further illustrated with examples involving differently oriented rectangles in an electric field, and the introduction of Gauss's Law is foreshadowed through an example involving a point charge and a spherical surface.

05:01

🌐 Gauss's Law and its Application to Symmetric Charge Distributions

This paragraph delves into Gauss's Law, which states that the electric flux through a closed surface is equal to the total charge enclosed divided by the permittivity of free space. The law is illustrated with examples of spherical, cylindrical, and planar symmetries. For spherical symmetry, the electric field inside and outside a uniformly charged thin shell is calculated. The cylindrical symmetry example involves an infinite line of charge, and the electric field at a point above the line is determined. Planar symmetry is exemplified by a uniformly charged infinite large horizontal plate, and the electric field in the vicinity of the plate is calculated. The paragraph explains how the electric field behaves in the presence of different symmetric charge distributions and how Gauss's Law can be applied to find the electric field in each scenario.

10:02

📡 Complex Applications of Gauss's Law with Parallel Plates

The final paragraph discusses a more complex scenario involving two infinitely large parallel plates with opposite surface charge densities. It explains how the electric field is determined in the space between and outside the plates using Gauss's Law and the superposition principle. The electric field lines and their directions are described, emphasizing that the field is zero outside the plates and constant between the plates. The summary concludes with a visual representation of the electric field lines, illustrating the principles discussed throughout the video script.

Mindmap

Keywords

💡Electric Flux

Electric flux is a measure of the electric field's influence passing through a given surface. Defined as the dot product of the electric field and the area vector perpendicular to the surface, it represents the total electric field lines penetrating the surface area. In the video, electric flux is the central theme, with examples illustrating how it varies depending on the orientation of the surface relative to the electric field.

💡Gauss's Law

Gauss's Law is a fundamental principle in electromagnetism that relates the electric flux through a closed surface to the total charge enclosed by the surface. It is expressed as the permittivity of free space times the net charge divided by the flux. The video explains how Gauss's Law is derived from the concept of electric flux and demonstrates its application in calculating electric fields around various symmetric charge distributions.

💡Electric Field

An electric field is a vector field that surrounds electrically charged particles and exerts a force on other charged particles within the field. In the context of the video, the electric field is the source of electric flux, and its magnitude and direction determine the amount of flux through a surface. The script uses the electric field to explain the concept of flux and its calculation through different surfaces.

💡Differential of Area (dA)

In the script, dA refers to a small element of area on a surface through which the electric field is considered to pass. It is treated as a vector quantity with a magnitude equal to the area of the element and a direction perpendicular to the surface. The differential of area is crucial for calculating the differential flux, dΦ, which is the product of the electric field and dA.

💡Permittivity of Free Space (ε₀)

The permittivity of free space, denoted as ε₀, is a fundamental physical constant that determines the strength of the electric field around a charge in a vacuum. In the video, ε₀ is used in the context of Gauss's Law to relate the total electric flux through a closed surface to the enclosed charge, showing that the flux is independent of the distance from the charge when considering a spherical surface.

💡Spherical Symmetry

Spherical symmetry refers to a situation where the charge distribution or the electric field is the same in all directions around a central point. The video uses spherical symmetry to demonstrate how Gauss's Law can be applied to calculate the electric field around a point charge, where the symmetry simplifies the calculation by ensuring uniform electric field strength over the surface of a sphere.

💡Cylindrical Symmetry

Cylindrical symmetry occurs when the charge distribution or electric field is uniform along the length of a cylinder and varies only with the radial distance from the cylinder's axis. The script explains how this type of symmetry allows for the application of Gauss's Law to calculate the electric field around an infinitely long line of charge.

💡Planar Symmetry

Planar symmetry is characterized by a uniform charge distribution across an infinite plane, resulting in an electric field that is constant in magnitude and direction perpendicular to the plane. The video describes how this symmetry simplifies the calculation of the electric field around an infinite charged plane using Gauss's Law.

💡Surface Charge Density

Surface charge density, often denoted by sigma (σ), is the amount of charge per unit area on a surface. In the video, surface charge density is used to describe the charge distribution on plates and other surfaces, and it plays a key role in determining the electric field around these surfaces according to Gauss's Law.

💡Superposition Principle

The superposition principle states that when multiple electric fields act on the same point, the resultant electric field is the vector sum of the individual fields. The video script uses this principle to explain the electric field between two parallel plates with equal but opposite surface charge densities, where the fields add up to produce a uniform electric field between the plates.

Highlights

Introduction to electric flux and Gauss's law, fundamental concepts in electromagnetism.

Electric flux defined as the rate of flow of electric field through a surface, applicable to both open and closed surfaces.

Explanation of differential of area (dA) and its role in calculating electric flux through small elements.

Total flux calculation as an integral over the entire area, with examples of positive and negative flux.

Unit of electric flux is newton meters squared per coulomb, emphasizing its scalar nature.

Demonstration of flux through differently oriented rectangles in an electric field.

Clarification of flux through a closed surface with normals pointing from inside to outside.

Total flux through a closed surface can be positive, negative, or zero, depending on the charge distribution.

Example of flux through a sphere with a point charge at its center, illustrating Gauss's law.

Gauss's law formula: Electric flux through a closed surface equals the enclosed charge divided by permittivity of free space.

Importance of symmetry in calculating electric fields using Gauss's law, with examples of spherical, cylindrical, and planar symmetry.

Calculation of electric field inside and outside a thin hollow sphere with uniformly distributed charge.

Cylindrical symmetry example with an infinite line of charge and the resulting electric field.

Planar symmetry and the calculation of electric field around an infinitely large charged plate.

Graphical representation of electric field magnitude versus distance for different symmetries.

Complex situation of two infinitely large parallel plates with opposite surface charge densities and the resulting electric field.

Superposition principle applied to calculate the total electric field between two charged plates.

Conclusion summarizing the importance of Gauss's law in electromagnetism and its applications.

Transcripts

Browse More Related Video

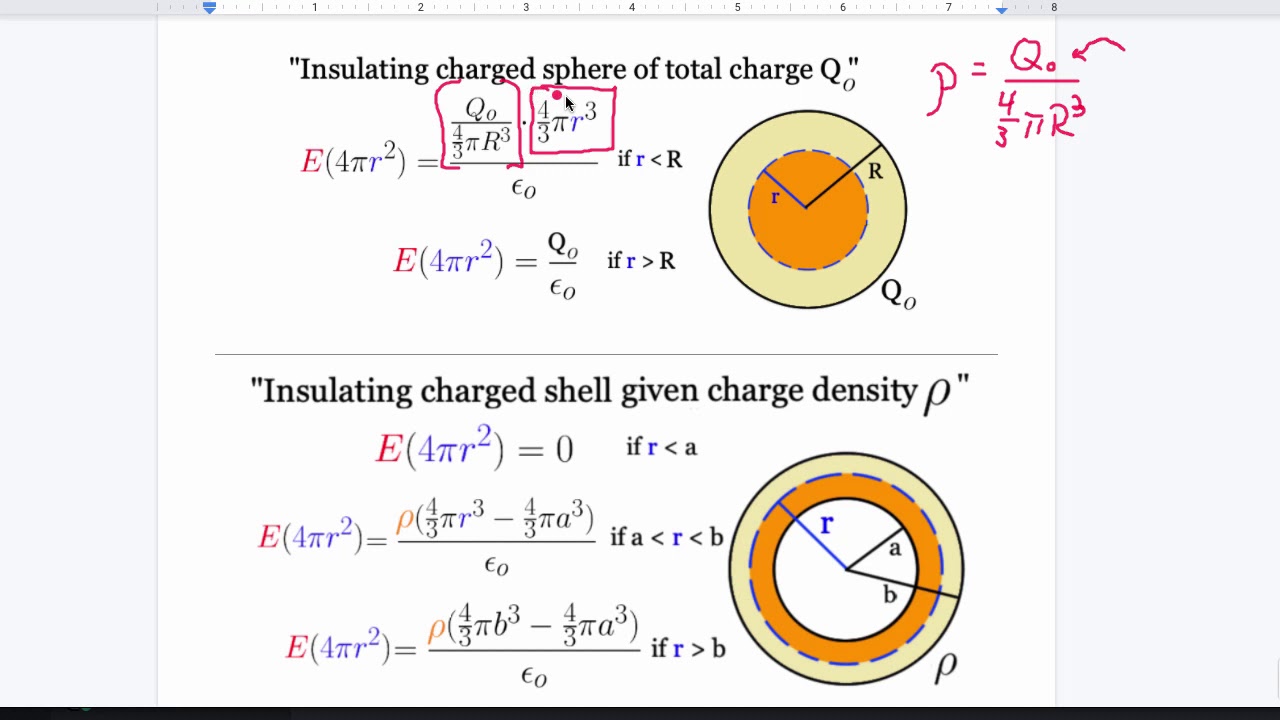
Ultimate Gauss' Law review

Gauss law of electricity | Electrostatics | Physics | Khan Academy

Gauss law logical proof (any closed surface) | Electric charges & fields | Physics | Khan Academy

Physics 37.1 Gauss's Law Understood (3 of 29) What is Gauss' Law?

Electric Flux (part 1)

Electric Flux, Gauss's Law & Electric Fields, Through a Cube, Sphere, & Disk, Physics Problems

Electric Flux and Gauss’s Law | Electronics Basics #6

Takeaways

Q & A

What is electric flux?

How is the differential of electric flux, dΦ, defined?

What is the unit of electric flux?

How does the orientation of a surface affect the electric flux through it?

What is the significance of the normal to a closed surface in calculating electric flux?

How is Gauss's Law related to electric flux?

What are the three types of symmetry that simplify the calculation of electric fields using Gauss's Law?

How does the electric field inside a hollow sphere with a uniformly distributed charge vary with distance from the center?

What is the formula for the electric field around an infinite line of charge with uniform linear charge density (λ)?

How does the electric field behave in the vicinity of a flat, infinite, large, horizontal plate with a uniform charge density (σ)?

What is the electric field between two infinitely large parallel plates with equal and opposite surface charge densities?