Electric Flux (part 1)
TLDRThe script introduces the concept of electric flux, a measure of electric field lines passing through a surface, using the analogy of sunlight through a window. It explains how flux is calculated by considering the electric field's magnitude, the area's orientation, and size. The explanation includes the formula for electric flux, \( \Phi_e = E \cdot A \cdot \cos(\theta) \), and discusses variations in flux due to non-uniform electric fields and the application of Gauss's law to closed surfaces, emphasizing the principle that no net flux occurs through a closed surface without an enclosed charge.
Takeaways
- 🌐 Electric flux is a concept used to calculate electric fields, introduced by Gauss.
- 📏 It represents the electric field lines passing through a surface, similar to how sunshine passes through a window.
- 🔴 The direction of the electric field lines (like red lines in the script) determines the direction of the test charge movement.
- 📊 The amount of electric flux through a surface depends on the electric field's intensity, the surface's orientation, and its area.
- 🌞 The more aligned the surface is with the electric field, the greater the flux, similar to how more sunlight enters a window facing the sun.
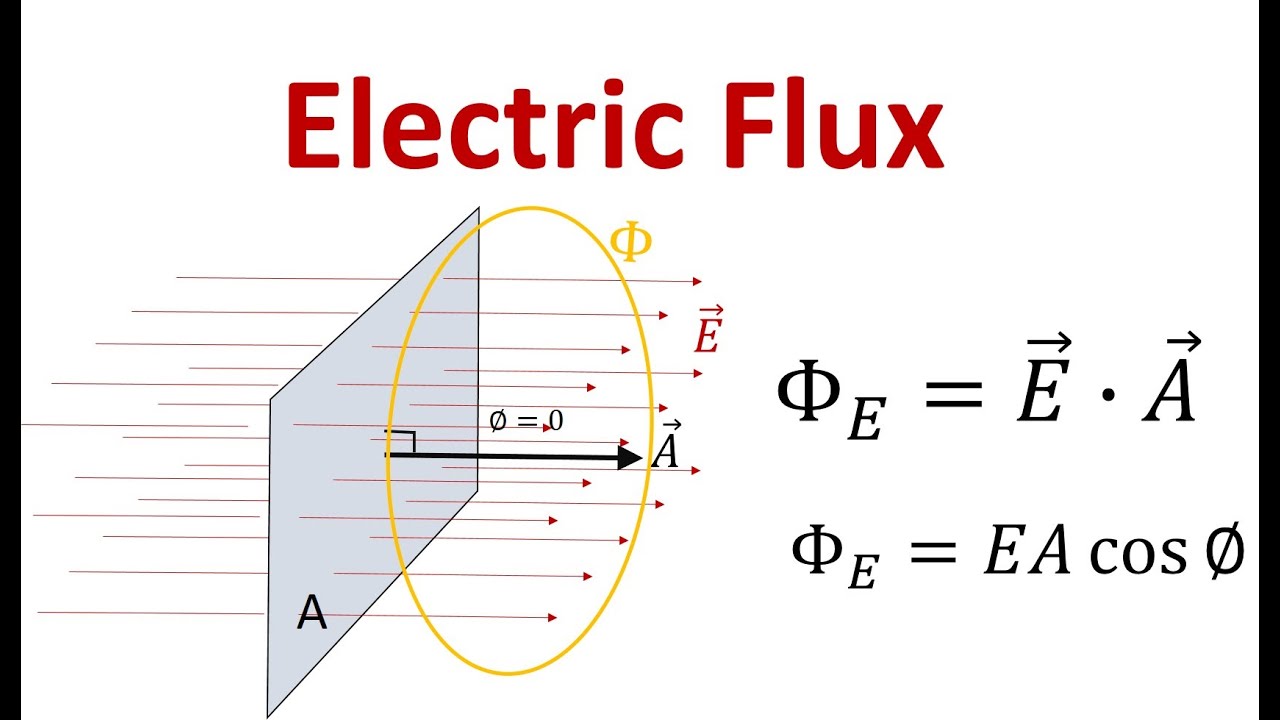
- 📐 Electric flux is calculated using the equation \( \Phi_e = E \cdot A \cdot \cos(\theta) \), where \( E \) is the electric field, \( A \) is the area, and \( \theta \) is the angle between the field and the area vector.
- 📈 For a uniform electric field, the flux is directly proportional to the area and the cosine of the angle between the field and the area vector.
- 🔄 In non-uniform fields, the flux is calculated by integrating the dot product of the electric field vector and the differential area vector over the entire surface.
- 🔮 For a closed surface, the direction of the differential area vector \( \mathbf{dA} \) is defined as being perpendicularly outward.
- 💡 Gauss's law states that for a closed surface enclosing no net charge, the net electric flux through it is zero, as the inward and outward fluxes cancel each other out.
- 🔧 The concept of electric flux is fundamental in understanding how electric fields interact with surfaces and is essential in solving problems involving electric fields.
Q & A
What is electric flux?
-Electric flux is a concept used to calculate the electric field flowing through a surface, analogous to the flow of sunshine through a window.
How does the orientation of a surface affect electric flux?
-The orientation of a surface affects the electric flux by determining how much electric field lines pass through it, similar to how a window's orientation affects the amount of sunlight entering.
What is the relationship between the electric field and electric flux?
-The electric field is analogous to the intensity of sunlight, and the electric flux is the amount of this 'sunlight' that passes through a surface.
What is a uniform electric field?
-A uniform electric field is one where the electric field lines are evenly spaced, indicating the same field strength at every point within the field.
How is electric flux calculated for a surface?
-Electric flux is calculated using the formula \( \Phi_e = \vec{E} \cdot \vec{A} \), where \( \vec{E} \) is the electric field vector and \( \vec{A} \) is the area vector perpendicular to the surface.
What does the dot product in the electric flux formula represent?
-The dot product in the formula represents the component of the electric field that is parallel to the area vector, effectively giving the scalar quantity of flux.
How does the angle between the electric field and the area vector affect the electric flux?
-The angle affects the electric flux through the cosine of the angle, where a smaller angle results in a larger component of the electric field being perpendicular to the area vector, thus increasing the flux.
What is the significance of Gauss's Law in relation to electric flux?
-Gauss's Law states that for a closed surface with no net charge enclosed, the net electric flux through the surface is zero, which is a fundamental principle in understanding electric fields.
How is electric flux calculated when the electric field is not uniform?
-In a non-uniform electric field, the flux through a surface is calculated by integrating the dot product of the electric field vector and the area vector over the entire surface.
What is the significance of the direction of the area vector for a closed surface?
-For a closed surface, the direction of the area vector is defined as being perpendicularly outward, which is important for calculating the net flux through the surface.
How does the presence of charge within a closed surface affect the net electric flux?
-If a closed surface encloses a net charge, the net electric flux through the surface will not be zero, as the electric field lines will terminate or originate from the charge.
Outlines
🔋 Understanding Electric Flux
This paragraph introduces the concept of electric flux, a fundamental idea in the study of electric fields, originally formulated by Gauss. The speaker uses the analogy of sunlight shining through a window to explain how electric flux is calculated through a surface. The electric field is likened to the sun's rays, and the window represents the surface area. The amount of 'sunshine' or electric flux that passes through is dependent on the intensity of the electric field, the orientation of the surface, and the size of the area. The paragraph also touches on the uniformity of the electric field and how it affects the calculation of flux.
📐 Calculating Electric Flux with Non-Uniform Fields
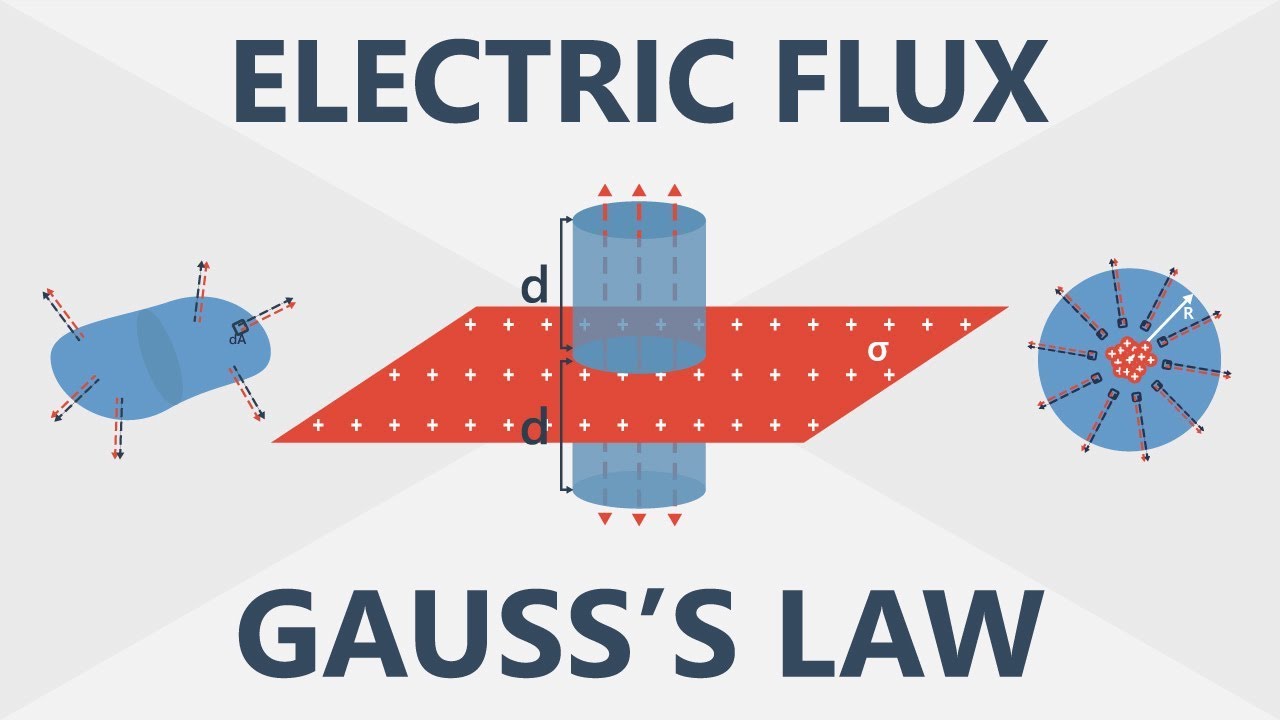
The second paragraph delves into the complexities of calculating electric flux when the electric field is not uniform across a surface. The speaker describes a scenario where the field's intensity varies, becoming stronger as one moves in a certain direction. To address this, the surface is divided into infinitesimally small areas, each represented by a vector \( \vec{da} \). The flux through each tiny area is calculated by taking the dot product of the electric field vector \( \vec{e} \) and the area vector \( \vec{da} \), and then summing these fluxes to find the total flux through the surface. The paragraph also discusses the implications for a closed surface, such as a sphere, where the direction of \( \vec{da} \) is always outward and perpendicular to the surface. It concludes with the Gauss's law principle that for a closed surface enclosing no net charge, the net flux through it will be zero.
Mindmap
Keywords
💡Electric Flux
💡Electric Field
💡Test Charge
💡Surface Area
💡Orientation
💡Sunshine Analogy
💡Vector Quantity
💡Dot Product
💡Uniform Electric Field
💡Closed Surface
💡Gauss's Law
Highlights
Introduction to electric flux as a concept created by Gauss to calculate electric fields.
Electric flux is calculated by determining the electric field traveling through a surface.
Analogy of electric field lines to the direction of movement of test charges, positive and negative.
Different surface orientations and their impact on electric flux calculation.
The concept of electric flux likened to the flow of sunshine through a window.
Factors affecting electric flux: intensity of the electric field, surface area, and orientation.
Explanation of the equation for electric flux, involving the electric field magnitude and area vector.
Clarification that electric flux is a scalar quantity resulting from the dot product.
Handling non-uniform electric fields by integrating the flux over small areas.
General formula for electric flux through a non-uniform field using integration.
Definition of electric flux through a closed surface and its properties.
Gauss's law implication that for a closed surface with no net charge, the net flux is zero.
The importance of the direction of da (vector area) for closed surfaces being outward.
The concept of flux cancellation in a closed surface with equal and opposite contributions.
Practical applications of understanding electric flux in various physical scenarios.
The significance of electric flux in the study of electromagnetism and field theory.
Final summary emphasizing the importance of understanding electric flux for analyzing electric fields.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: