How To Draw Electric Field Lines of Point Charges - College Physics
TLDRThe video script discusses the concept of electric fields and their representation through electric field lines. It explains that the direction of these lines indicates the type of charge: positive charges have lines emanating from them, while negative charges have lines pointing towards them. The density of the lines reflects the strength of the electric field, with more lines indicating a stronger field. The script also covers the calculation of the electric field using the equation E=kQ/R^2, where k is the electrostatic constant, Q is the charge, and R is the distance from the charge. It further illustrates how to determine the charges of different points based on the number of electric field lines and how electric fields interact between multiple charges and charged plates.
Takeaways
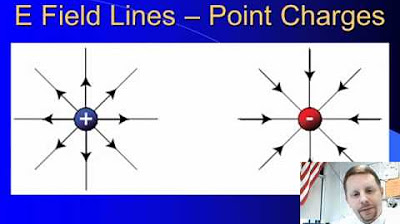
- 📌 The direction of electric field lines indicates the type of charge; lines emanate from positive charges and point towards negative charges.
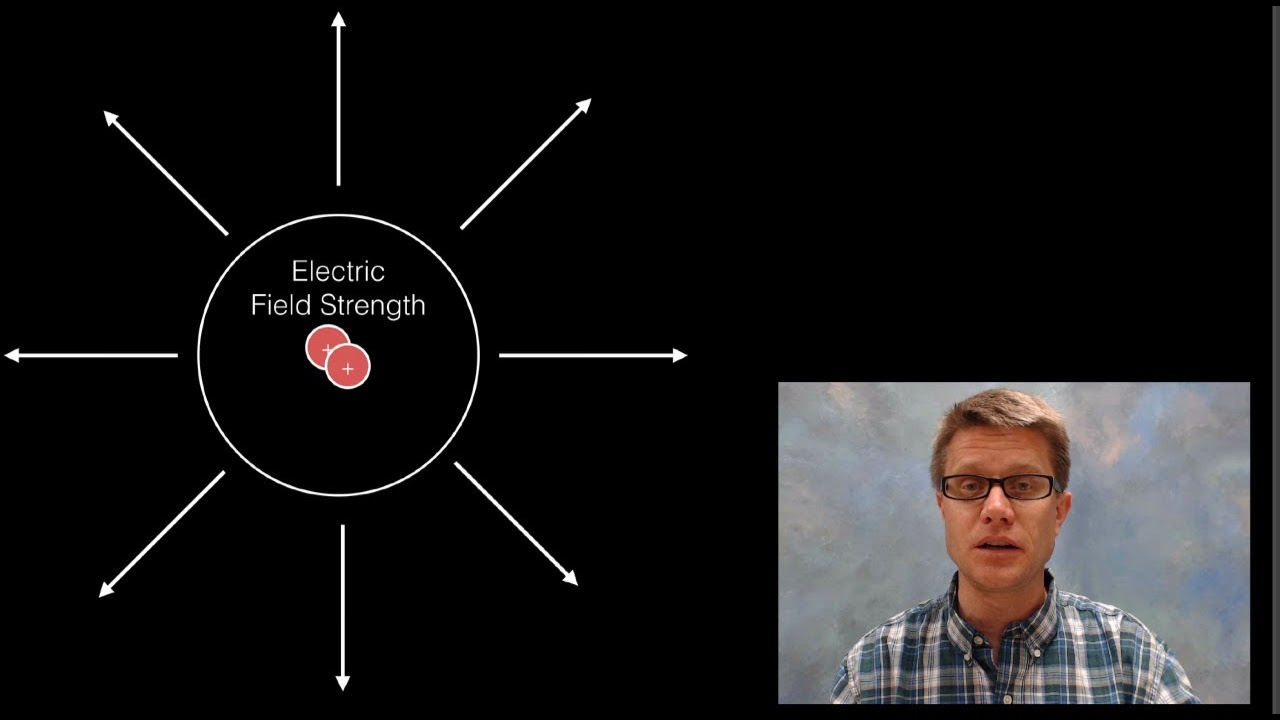
- 🔍 The density of electric field lines represents the strength of the field; more lines in a region indicate a stronger field.
- 🌐 The electric field at a point P due to a point charge Q is calculated using the equation E = k * Q / R^2, where k is the electrostatic constant, Q is the charge, and R is the distance from the charge to point P.
- 🚫 Electric field lines do not cross each other; intersections are not physically meaningful.
- 🔡 The number of electric field lines can be used to determine the relative magnitudes of point charges when compared to a known reference.
- ➡️ When two like charges repel each other, their electric field lines bend away from each other, resulting in a cancellation effect at the midpoint between them.
- 🔄 The resultant electric field vector at a point is found by adding the individual field vectors from nearby charges.
- 🔌 For parallel plates with opposite charges, the electric field lines are uniform and straight within the interior of the plates, and bulge at the edges.
- 📈 The electric field lines from a point charge to a charged plate follow the charge's nature: lines start at the positive charge and end at the negative plate, bending as they approach the plate.
- 📚 Understanding electric field lines and their properties is crucial for visualizing and calculating the effects of electric charges in various configurations.
Q & A
What is the basic rule for the direction of electric field lines around a positive charge?
-The electric field lines emanate away from a positive charge.
How do electric field lines behave around a negative charge?
-Electric field lines point towards a negative charge.
What does the density of electric field lines indicate about the electric field strength?
-The density of electric field lines is directly proportional to the strength of the electric field. More lines in a given region of space indicate a stronger electric field.
What is the equation used to calculate the electric field due to a point charge?
-The equation used to calculate the electric field due to a point charge is E = k * Q / R^2, where E is the electric field, k is the electrostatic constant (approximately 9 * 10^9 N m^2/C^2), Q is the charge, and R is the distance from the point charge to the point of interest.
How can you determine the magnitude and sign of a charge based on the electric field lines?
-The direction of the electric field lines helps determine the sign of the charge (positive or negative), and the number of lines in a region can give an idea of the magnitude relative to a known charge.
What happens to the electric field lines between two equal positive charges?
-Between two equal positive charges, the electric field lines will point away from each charge and will cancel each other out in the middle, resulting in zero electric field at the midpoint.
How do electric field lines behave around two positive charges of unequal magnitudes?
-The electric field lines will point away from the positive charges and have a greater density (more lines) coming from the charge with the larger magnitude.
What is the characteristic of electric field lines between a positive point charge and a negatively charged plate?
-The electric field lines will start at the positive point charge and bend towards the negatively charged plate, becoming relatively horizontal as they get closer to the plate.
What is the basic principle behind drawing electric field lines for charged parallel plates?
-For charged parallel plates, the electric field lines will be relatively constant and straight within the interior of the plates, and they will point from the positively charged plate to the negatively charged plate.
Why do electric field lines never cross each other?
-Electric field lines never cross each other because each line represents a unique direction of the electric field vector at that point in space. If they were to cross, it would imply two different directions for the field at a single point, which is not possible.
How can you visualize the resultant electric field vector at a point between two charges?
-To visualize the resultant electric field vector at a point between two charges, you can break down the electric field vectors from each charge into their x and y components, add the components together, and then determine the overall direction and magnitude of the combined electric field at that point.
Outlines
🔋 Understanding Electric Fields and Charges
This paragraph introduces the concept of electric fields and their relationship with charges. It explains that electric field lines radiate outward from positive charges and point towards negative charges. The direction of these lines indicates the type of charge present. The paragraph also presents the equation for calculating the electric field (E = kQ/R^2) from a point charge, where k is the electrostatic constant, Q is the charge, and R is the distance from the charge. The concept of electric field line density is introduced, indicating that a higher density of lines represents a stronger electric field.
🧠 Calculating Charges and Electric Field Lines
The second paragraph focuses on calculating the charges of different points based on the number of electric field lines. It explains how to determine the magnitude and sign of charges by comparing the number of lines to a reference charge. The example given involves charges A, B, C, D, and E, with specific attention to how the electric field lines interact with positive and negative charges. The summary emphasizes understanding the direction of the electric field and using it to deduce the nature and magnitude of the charges involved.
🤔 Interaction of Electric Fields from Multiple Charges
This paragraph delves into the interaction of electric fields from multiple charges, specifically two positive point charges and their effect on the electric field in the space between them. It explains how the electric field vectors from two like charges will cancel each other out in certain regions, resulting in a zero electric field. The paragraph also discusses how to draw electric field lines for two positive charges of equal magnitude and for a positive charge interacting with a negative charge. The explanation includes the direction and curvature of the electric field lines based on the charges' nature and their relative positions.
📏 Electric Fields in Parallel Plates and Point-Plate Configurations
The final paragraph discusses the behavior of electric fields between parallel plates and between a point charge and a charged plate. It describes how electric field lines are relatively constant between the plates and how they bulge at the edges. The paragraph also explains how to draw electric field lines when a point charge is in proximity to a charged plate, emphasizing the influence of the charges and the configuration on the resulting field pattern. The summary highlights the importance of understanding electric field lines' behavior in different scenarios for a comprehensive grasp of electric fields.
Mindmap
Keywords
💡Electric Field
💡Point Charge
💡Electric Field Lines
💡Charge Magnitude
💡Direction of Electric Field
💡Density of Electric Field Lines
💡Positive Charge
💡Negative Charge
💡Electric Field Calculation
💡Parallel Plates
💡Vector Addition
Highlights
Electric field lines emanate from a positive charge and point towards a negative charge.
The direction of the electric field lines indicates the type of charge; away from positive and towards negative.
The equation to calculate the electric field from a point charge is $E = rac{kQ}{r^2}$, where $Q$ is the charge and $r$ is the distance from the charge.
The density of electric field lines is related to the strength of the electric field; more lines indicate a stronger field.
Electric field lines do not cross each other, signifying unique paths of force.
By comparing the number of electric field lines, one can determine the relative magnitudes of charges.
Positive charges have electric field lines that radiate outward, while negative charges have lines converging towards them.
When two positive charges are close to each other, their electric field lines will point away from each other and cancel in the middle.
The resultant electric field vector is found by adding the individual vectors from multiple charges.
Electric field lines from positive charges bend away when near a negative charge, and vice versa.
For two charged parallel plates, the electric field lines are straight and uniform within the interior and bulge at the edges.
When a point charge is near a charged plate, the electric field lines from the point charge will bend towards the plate.
The number of electric field lines can be used to determine the sign and magnitude of unknown charges relative to a known charge.
Understanding electric field lines and their interactions is crucial for visualizing and calculating the effects of electric charges.
The electric field vector's direction is influenced by the proximity and sign of other charges, leading to field line bending.
In a scenario with multiple charges, the resultant electric field is the vector sum of the individual fields from each charge.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: