Electric Field, Force, Potential, Potential Energy (AP Physics SuperCram Review)
TLDRThis educational script explores the fundamental concepts of electric fields and potentials created by point charges. It explains how a positive charge generates a radially outward electric field, measured in Newtons per Coulomb, and how to calculate it using the formula \( KQ / R^2 \). The script also delves into electric potential, a scalar quantity measured in Joules per Coulomb, and its calculation with \( KQ / R \). It further discusses the relationship between electric force, potential energy, and the work-energy principle, highlighting the importance of vector components in calculating total electric fields and the significance of equipotential lines and field lines in visualizing electric fields. The summary also touches on the behavior of charges in electric fields, the concept of electric dipoles, and practical applications such as capacitors and electron acceleration.
Takeaways
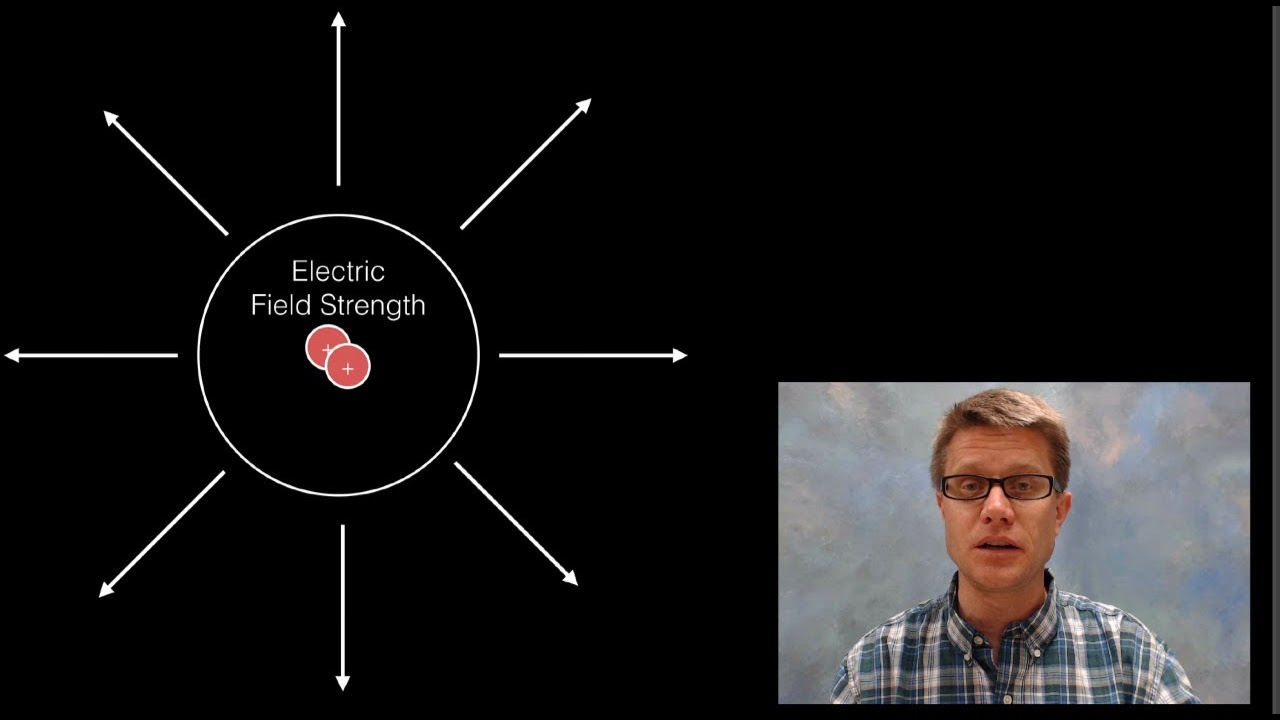
- 🔋 A point charge Q creates an electric field in every direction around it, with the field pointing outward if the charge is positive.
- 📏 The electric field's strength can be calculated using the formula \( E = \frac{kQ}{R^2} \), where E is the field strength, k is Coulomb's constant, Q is the charge, and R is the distance from the charge.
- 📍 The units of electric field are Newtons per Coulomb (N/C), indicating the force on a 1 C charge at a given point.
- 📚 Electric fields are vectors, requiring component analysis when multiple charges are involved, using the Pythagorean theorem for vector addition.
- 🌐 Electric potential (V) is a scalar quantity, measured in joules per Coulomb (J/C), representing potential energy per unit charge.
- 🔢 The electric potential at a point due to a charge can be found using \( V = \frac{kQ}{R} \), without worrying about vector directions.
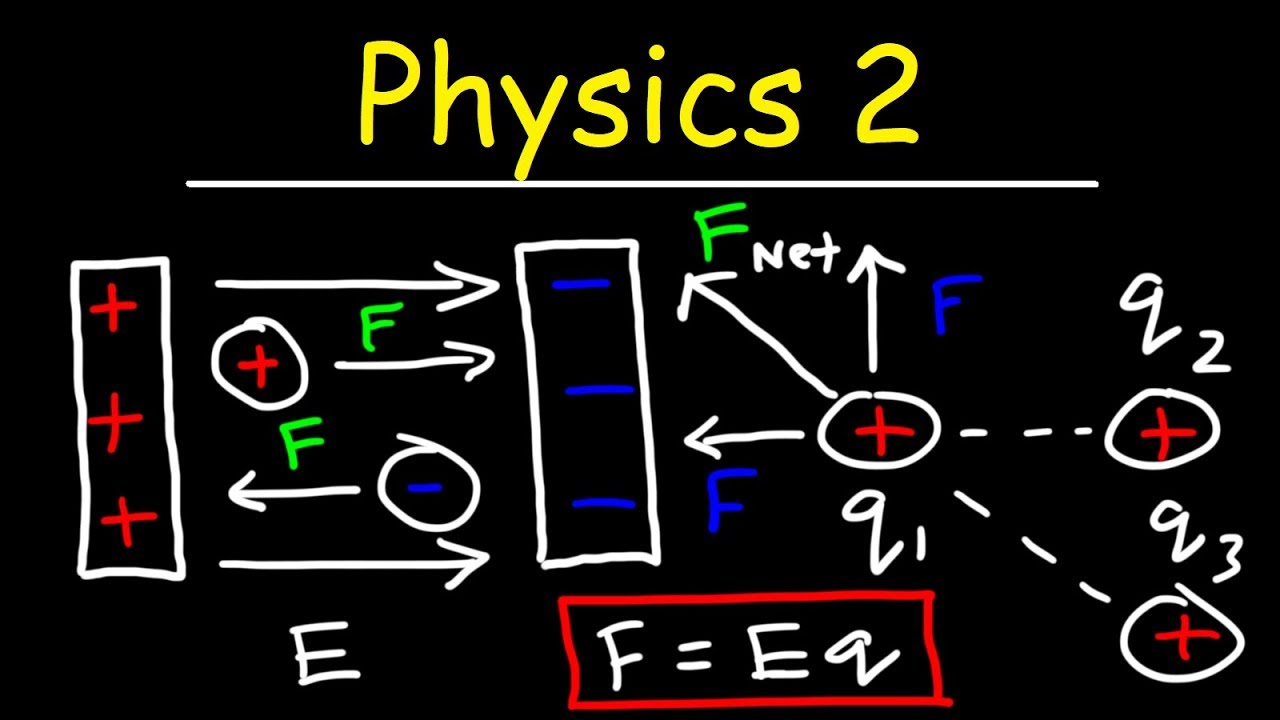
- ⚡ The electric force (F) between two charges can be calculated with \( F = k \frac{Q_1 Q_2}{r^2} \), but if the electric field (E) is known, \( F = Q \cdot E \) is simpler.
- 🔋 Electric potential energy (U) between two charges is given by \( U = k \frac{Q_1 Q_2}{r} \), or more simply, \( U = Q \cdot V \) if the potential is known.
- ⚡️ The direction of the electric field is from higher to lower potential, as indicated by the negative sign in the formula relating field to potential, \( E = -\frac{\Delta V}{\Delta x} \).
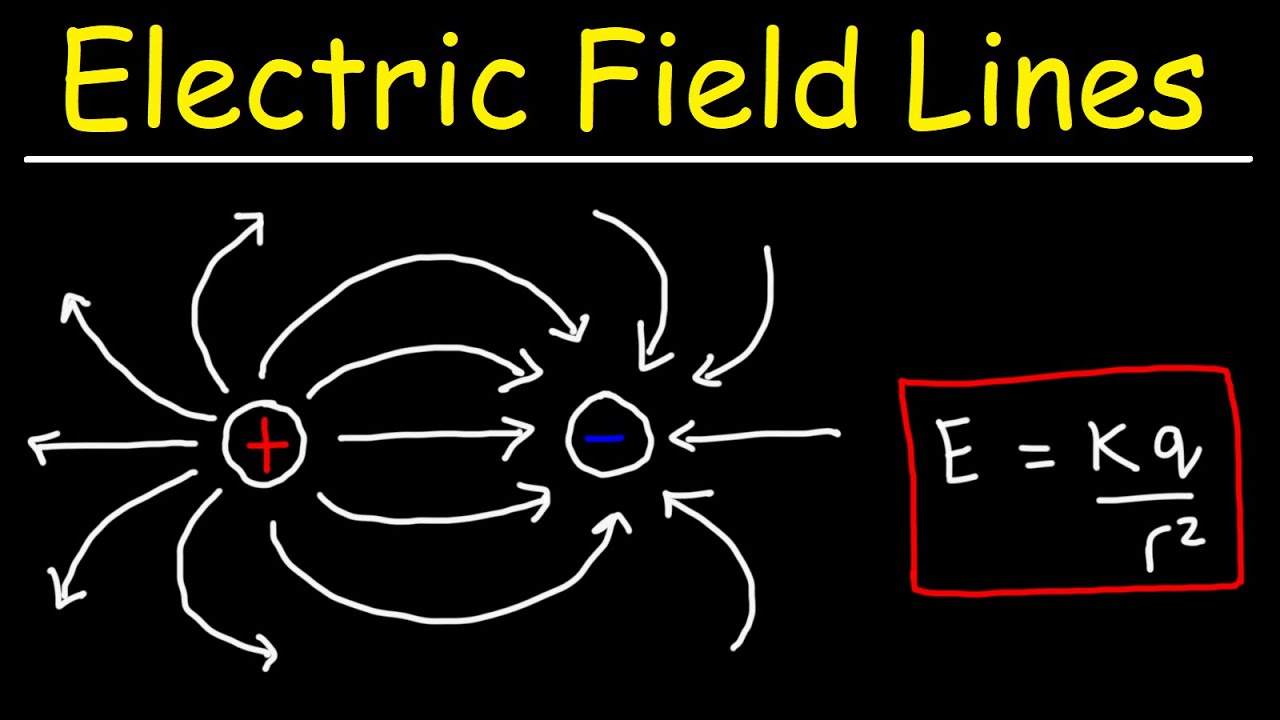
- 📈 Electric field lines are radial and outward from positive charges, and inward towards negative charges, with the density of lines indicating field strength.
- 📊 Equipotential lines are perpendicular to electric field lines and represent constant electric potential, being closely packed where the field is strongest.
Q & A
What is an electric field created by a point charge Q?
-An electric field is a region around a point charge Q where a force would be exerted on other charges. If the charge is positive, the electric field points radially outward from the charge.
What are the units of the electric field?
-The units of the electric field are Newtons per Coulomb (N/C), indicating the force on a one Coulomb charge placed at that point.
How is the magnitude of the electric field created by a point charge calculated?
-The magnitude of the electric field is calculated using the formula \( E = \frac{kQ}{R^2} \), where \( k \) is Coulomb's constant, \( Q \) is the charge creating the field, and \( R \) is the distance from the charge to the point in space.
Why is it necessary to break the electric field into components when multiple charges are present?
-When multiple charges are present, their individual electric fields contribute to the total electric field at a point. To find the total electric field, one must break down the fields into components and sum the X and Y components using the Pythagorean theorem.
What is electric potential and how is it different from electric field?
-Electric potential is a scalar quantity that represents the potential energy per unit charge at a point in space, measured in joules per coulomb (J/C). Unlike the electric field, which is a vector and has direction, electric potential has no direction and no components.
How is the electric potential created by a point charge calculated?
-The electric potential is calculated using the formula \( V = \frac{kQ}{R} \), where \( k \) is Coulomb's constant, \( Q \) is the charge, and \( R \) is the distance from the charge to the point in space.
What is the relationship between electric potential and electric potential energy?
-The electric potential energy between two point charges is the product of the charge and the electric potential at the point where the second charge is located, given by \( E_{PE} = qV \), where \( q \) is the charge and \( V \) is the electric potential.
How do you determine the direction of the electric force on a positive and negative charge in an electric field?
-The electric force on a positive charge points in the direction of the electric field, while the force on a negative charge points in the opposite direction of the electric field.
What is the formula that relates the electric field to the electric potential?
-The formula that relates the electric field to the electric potential is \( E = -\frac{\Delta V}{\Delta x} \), indicating that the electric field points toward lower electric potential.
How is the electric field in the region between the plates of a parallel plate capacitor determined?
-The electric field between the plates of a parallel plate capacitor is determined using the formula \( E = \frac{\Delta V}{\Delta x} \), which simplifies to \( E = \frac{\epsilon}{D} \), where \( \epsilon \) is the permittivity of the medium and \( D \) is the distance between the plates.
What is the stopping potential and how is it related to the kinetic energy of a charge?
-The stopping potential is the voltage required to stop a moving charge. It is related to the kinetic energy of the charge by the equation \( \Delta E_{PE} = \frac{1}{2}mv^2 \), where the change in electric potential energy equals the change in kinetic energy.
Outlines
🔋 Understanding Electric Fields and Electric Potential
This paragraph explains the concept of electric fields generated by a point charge Q. A positive charge creates an electric field that radiates outward. The electric field's units are Newtons per Coulomb, indicating the force on a one Coulomb charge at a specific point. The electric field's magnitude can be calculated using the formula KQ/R². Since the electric field is a vector, it needs to be broken into components to find the total electric field from multiple charges. Additionally, the paragraph discusses electric potential (V), a scalar quantity measured in Joules per Coulomb, which indicates the potential energy of a one Coulomb charge at a point. The electric potential can be calculated using KQ/R, and the relationship between electric potential and electric field is given by ΔV/ΔX. The paragraph concludes by highlighting that a charge will experience an electric force (F) based on the electric field, with the direction of the force depending on the charge's sign.
📊 Calculating Electric Fields and Potentials in Complex Systems
This paragraph delves into the process of calculating the electric field and electric potential in more complex configurations. It explains the method to find the total electric field at a specific point due to multiple charges, involving the use of the Pythagorean theorem and trigonometric functions to resolve vectors into components. The paragraph emphasizes that electric potential calculations are simpler because electric potential is not a vector. It also explains the concept of electric field lines and equipotential lines, noting that field lines point radially outward from positive charges and inward toward negative charges. Equipotential lines are always perpendicular to electric field lines, and their density indicates the strength of the electric field. The paragraph concludes by discussing the electric field between parallel plate capacitors, using the formula ΔV/ΔX, and the concept of stopping potential for charged particles in electric fields.
Mindmap
Keywords
💡Point Charge
💡Electric Field
💡Coulomb's Law
💡Electric Potential
💡Vector
💡Components
💡Pythagorean Theorem
💡Equipotential Lines
💡Electric Dipole
💡Electric Potential Energy
💡Parallel Plate Capacitor
Highlights
A point charge Q creates an electric field radially outward if positive and inward if negative.
Electric field units are Newtons per Coulomb, indicating force on a one Coulomb charge.
The formula KQ over R squared is used to calculate the electric field size.
Electric fields are vectors and require component analysis for total field calculation.
Electric potential V is a scalar, measured in joules per Coulomb, indicating potential energy.
The formula KQ over R determines electric potential created by a point charge.
Positive charges create positive electric potential, and negative charges create negative.
Electric force between two charges is calculated using F = K * Qq / r squared.
Newton's third law ensures equal and opposite forces between interacting charges.
Electric force can also be found using F = Q * E, a simpler method when the electric field is known.
Electric potential energy between two charges is calculated with U = Q * V.
The relationship between electric field and potential is given by ΔV / Δx.
Electric field lines point toward lower electric potential and never cross.
Equipotential lines are perpendicular to electric field lines and indicate constant potential.
For a parallel plate capacitor, the electric field is uniform and points from positive to negative.
The speed of an electron moving between capacitor plates can be calculated using energy conservation.
The stopping potential can be determined for a charge coming to rest due to a voltage.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: