Electric Field (1 of 3) An Explanation

Step by Step Science
12 Feb 201410:06
EducationalLearning
32 Likes 10 Comments

TLDRThis video introduces the concept of the electric field, emphasizing its definition as the force per unit charge. It explains the direction of the electric field around a charge, using a test charge to demonstrate that the field points away from positive charges and towards negative ones. The video also touches on the magnitude of the electric field, illustrating it with the density of electric field lines. The formula for calculating the electric field is introduced, highlighting its dependence on the charge and the distance from the charge. The distinction between electric field and electric force is clarified, and the video encourages watching the next installment for practical calculations.

Takeaways
  • 📚 The electric field is defined as the force per unit of charge, and it has both magnitude and direction.
  • 🧭 To determine the direction of the electric field, use a test charge (a small positive charge) and observe the direction of the force it would experience in the presence of the main charge.
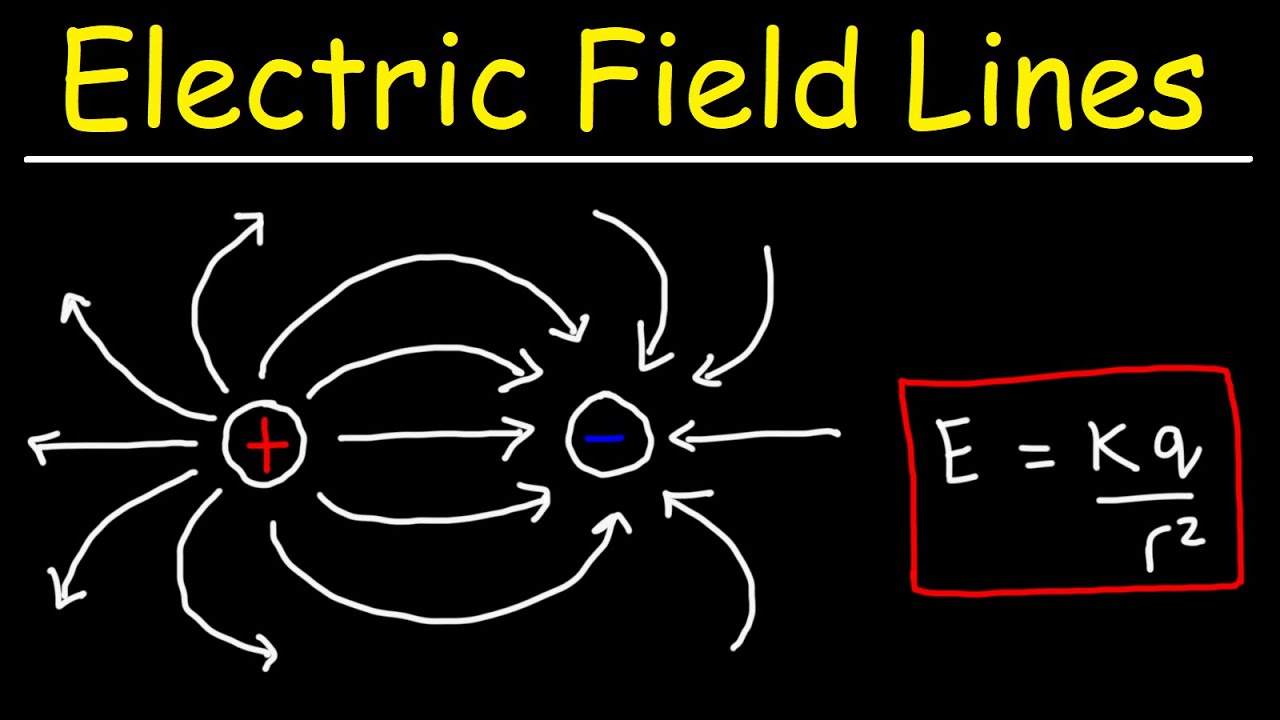
  • 🔋 The direction of the electric field around a positive charge is away from it, while around a negative charge, it points towards the charge.
  • 🌐 The magnitude of the electric field can be visually represented by the density of electric field lines; closer to the charge, the lines are denser, indicating a stronger field.
  • 🔢 The equation for the electric field is E = kQ/d^2, where E is the electric field, k is Coulomb's constant, Q is the charge of the main charge, and d is the distance from the charge.
  • 🔄 The electric field is a vector quantity, meaning it has both magnitude and direction, and is distinct from the electric force described by Coulomb's law.
  • 🔧 The electric field only requires one charge to exist, whereas the electric force between two charges is governed by Coulomb's law with the formula F = k(q1 * q2)/d^2.
  • 📈 The strength of the electric field is inversely proportional to the square of the distance from the charge, meaning it weakens as you move away from the charge.
  • 🔍 The electric field can be calculated at any point by using the charge present at that point and the distance from the main charge.
  • 🤝 The relationship between the electric field and the force on a charge is given by F = qE, where F is the force, q is the charge, and E is the electric field.
  • 🎓 Understanding the concepts of electric field and electric force, as well as their differences and relationships, is crucial for comprehending electromagnetic interactions.
Q & A

  • What is the primary focus of the video?

    -The primary focus of the video is to introduce the concept of the electric field, specifically discussing how to determine its direction and magnitude without performing any calculations.

  • What is the definition of an electric field?

    -The electric field is defined as the force per unit of charge. It is a vector quantity, meaning it has both magnitude and direction.

  • How is the direction of an electric field determined around a charge?

    -The direction of the electric field around a charge is determined by using a test charge, which is a small positive charge. The direction of the force on the test charge indicates the direction of the electric field. For a positive main charge, the electric field points away from the charge, and for a negative main charge, it points towards the charge.

  • What is a test charge used for?

    -A test charge is used to determine the direction of the electric field at a particular point in space. It is a hypothetical, very small positive charge that, when placed in an electric field, experiences a force whose direction indicates the electric field's direction.

  • How can the magnitude of the electric field be qualitatively represented?

    -The magnitude of the electric field can be qualitatively represented by the density of electric field lines. The closer the lines are to each other, the stronger the electric field; conversely, the farther apart they are, the weaker the electric field.

  • What is the difference between the electric force and the electric field?

    -The electric force refers to the force experienced by a charged particle due to the presence of other charges, as described by Coulomb's Law. The electric field, on the other hand, is a field that exists around a charge and describes the force per unit charge that would be experienced by a small test charge placed in that field.

  • What is the equation for the electric field?

    -The equation for the electric field E is given by E = k * Q / d^2, where k is Coulomb's constant, Q is the charge creating the electric field, and d is the distance from the charge.

  • How does the electric field strength change with distance from the charge?

    -The electric field strength is inversely proportional to the square of the distance from the charge. As you move farther away from the charge, the electric field becomes weaker, and as you get closer, it becomes stronger.

  • What is the relationship between the electric field and the force experienced by a charge?

    -The force experienced by a charge in an electric field is given by F = E * q, where F is the force, E is the electric field strength, and q is the charge experiencing the force. This relationship shows that the force is directly proportional to the electric field strength and the amount of charge.

  • Why is it important to understand the difference between electric force and electric field?

    -Understanding the difference between electric force and electric field is important because it allows us to correctly analyze and calculate the interactions between charges. The electric field describes the potential influence on a charge, while the electric force is the actual interaction experienced by the charge. This distinction is crucial for accurately modeling and predicting electrical behavior in various scenarios.

  • What is suggested for viewers to better understand electric fields?

    -The video suggests that viewers should watch both the introduction video and the next video, where simple electric field calculations will be performed. This will provide a comprehensive understanding of how electric fields work.

Outlines
00:00
🌟 Introduction to Electric Fields

This paragraph introduces the concept of electric fields, emphasizing the importance of understanding both direction and magnitude. It clarifies that electric fields are vector quantities with both magnitude and direction. The video aims to explain how to determine the direction of the electric field around a charge, using the concept of a test charge, which is a small positive charge used to probe the field without disrupting it. The direction of the electric field is established as being away from positive charges and towards negative charges. The magnitude of the electric field is qualitatively described by the density of electric field lines, with stronger fields indicated by closer lines and weaker fields by lines that are further apart.

05:00
📝 Equations and Calculation of Electric Fields

This paragraph delves into the mathematical representation of electric fields, starting with the fundamental equation for electric field strength, which involves Coulomb's constant (K), the charge (Q), and the distance from the charge. It distinguishes between the electric field and the electric force, highlighting that an electric field can exist with just one charge, whereas a force requires two. The explanation continues with how to derive the electric field equation and how it relates to the force experienced by a test charge placed in the field. Additionally, the paragraph introduces another form of the electric field equation that allows for calculating the force on a charge based on the electric field strength and the charge's quantity. The summary encourages watching the next video for further calculations and reiterates the importance of understanding the difference between electric force and electric fields.

Mindmap
Keywords
💡Electric Field
The electric field is a region around a charged particle where an electric force is exerted on other charged particles. It is a vector quantity, meaning it has both magnitude and direction. In the video, the electric field is introduced as the force per unit charge and is represented graphically by arrows pointing away from a positive charge and towards a negative charge.
💡Magnitude
In the context of the electric field, magnitude refers to the strength or intensity of the field. The magnitude is related to the density of electric field lines; closer to the charge, the lines are denser, indicating a stronger field, and farther away, the lines are more spread out, indicating a weaker field. The magnitude can be calculated using the equation E = kQ/d^2, where E is the electric field strength, k is Coulomb's constant, Q is the charge, and d is the distance from the charge.
💡Direction
The direction of the electric field is the direction in which a positive test charge would be pushed or pulled. For a positive charge, the electric field lines point away from it, and for a negative charge, the lines point towards it. This direction is crucial for understanding how charges interact within an electric field.
💡Test Charge
A test charge is a hypothetical small positive charge used to probe the electric field around another charge. It is assumed to be so small that it does not disturb the electric field of the main charge. The direction of the force on the test charge indicates the direction of the electric field at that point.
💡Coulomb's Law
Coulomb's Law quantifies the amount of force between two point charges. It states that the force is directly proportional to the product of the magnitudes of the charges and inversely proportional to the square of the distance between them. The law is used to calculate the electric force and is fundamental to understanding electric fields.
💡Vector
A vector is a quantity that has both magnitude and direction. In physics, vectors are used to describe quantities like force and velocity that have both size and direction components. The electric field is a vector because it has a direction (away from positive charges and towards negative charges) and a magnitude (the strength of the field).
💡Charge
Charge is a fundamental property of matter that causes it to experience a force when placed in an electromagnetic field. There are two types of电荷: positive and negative. Like charges repel each other, while opposite charges attract. The presence of charge is what creates an electric field.
💡Force
In physics, force is any action that causes an object to accelerate or change its motion. The force between charged particles, as described by Coulomb's Law, is an example of an electric force. The electric field is defined as the force per unit charge, which means it describes how much force a charged particle would experience if placed in the field.
💡Density of Electric Field Lines
The density of electric field lines is a visual representation of the strength of the electric field. Where the lines are closer together, the electric field is stronger, and where they are further apart, the field is weaker. This graphical representation helps in understanding the variation in the electric field's strength around a charge.
💡Calculations
Calculations in the context of the video refer to the mathematical process of determining the electric field's strength and direction using the provided equations and principles. These calculations are essential for understanding and predicting the behavior of electric fields and the forces they exert on charges.
💡Introduction
The introduction in this context refers to the initial part of the video where the presenter sets the stage for the topic to be discussed. It provides a foundation for the viewer to understand the subsequent content, which in this case is the concept of the electric field, its direction, and magnitude.
Highlights

Introduction to the concept of the electric field

Explaining the direction and magnitude of the electric field without calculating magnitudes

Emphasizing the importance of understanding electric fields and forces

Clarification that electric field is the force per unit charge and is a vector quantity

Definition of electric field in relation to a single charge

Difference between electric force and electric field

Use of a test charge to determine the direction of the electric field

Direction of the electric field around a positive charge

Direction of the electric field around a negative charge

Representation of the electric field's magnitude with field lines

Equation for the electric field and its components

Explanation of how to derive the electric field equation

Relation between the electric field and the force on a charge

Application of the electric field equation to calculate force on a charge

Advice to watch the next video for electric field calculations

Summary of the differences between electric force and electric field

Encouragement for viewers to engage and interact through likes and comments

Transcripts

Browse More Related Video

Electric Force

How To Draw Electric Field Lines of Point Charges - College Physics

Gauss Law Problems - Infinite Sheet of Charge and Parallel Plate Capacitor - Physics

High School Physics - Electric Fields

Electric Fields: Crash Course Physics #26

Gauss Law Problems, Cylindrical Conductor, Linear & Surface Charge Denisty, Electric Field & Flux,

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
ElectricFieldsPhysicsEducationVectorQuantitiesChargeInteractionsElectricForceFieldDirectionFieldMagnitudeCoulomb'sLawConceptualClaritySTEMLearning