4. Gauss's Law and Application to Conductors and Insulators
TLDRThe video script is a detailed lecture on Gauss's Law, an essential principle in electromagnetism. The professor begins by revisiting Gauss's Law, emphasizing its importance and providing a visual representation of electric field lines emanating from a point charge. The content delves into the mathematical derivation of the law, explaining the concept of line density and its relationship with the electric field. The professor illustrates how the electric field's strength is proportional to the charge and inversely proportional to the square of the radius, a fundamental aspect of Coulomb's Law. The lecture progresses to apply Gauss's Law to calculate the electric field around various charge distributions, including point charges, spherical shells, and infinite lines of charge. It also addresses the behavior of electric fields in conductors, explaining how charges redistribute within a conductor to eliminate the internal electric field, leading to a surface charge density that can be calculated using Gauss's Law. The script concludes with a brief overview of performing multiple integrals in Cartesian and polar coordinates, providing a simple example of calculating the area of a triangle using these methods.
Takeaways
- 📐 Gauss's Law is essential for understanding how to calculate the electric field around various charge distributions without performing complex integrals.
- 🌐 The visualization of electric field lines is crucial in applying Gauss's Law, as they must be symmetrical to the charge distribution causing them.
- 🔵 For a point charge, the electric field lines are radially outward, and the number of lines per unit charge is fixed by convention.
- 📈 The electric field's strength at a distance 'r' from a point charge is proportional to the charge 'q' and inversely proportional to 'r^2'.
- 📊 Gauss's Law states that the total electric flux through a closed surface is equal to the total charge enclosed divided by the vacuum permittivity (ε_0).
- 🧲 The electric field inside a conductor in a static situation is always zero because free electrons will rearrange to cancel any internal electric field.
- 🚫 Charges in a conductor reside on the outer surface and not within the conductor, regardless of the conductor's shape or if it contains holes.
- 🔋 The electric field just outside the surface of a conductor is perpendicular to the surface, and its magnitude is determined by the surface charge density.
- 📦 For a hollow conductor, the electric field inside is zero, which can be understood by considering the cancellation of fields due to symmetrical charge distributions.
- ⚖️ The principle of superposition allows for the calculation of the electric field due to multiple charges by simply summing the fields from each individual charge.
- 🧮 In cases where the symmetry of the charge distribution allows, Gauss's Law can simplify the calculation of electric fields by using appropriate Gaussian surfaces.
Q & A
What is Gauss's Law and why is it important in understanding electromagnetism?
-Gauss's Law, also known as Gauss's flux theorem, is a fundamental law of electromagnetism that relates the electric flux through a closed surface to the enclosed electric charge. It is important because it provides a way to calculate the electric field due to a charge distribution, and it is a direct consequence of the inverse-square law of electrostatic interactions. The law states that the total electric flux through a closed surface is proportional to the total charge enclosed by the surface.
How does the symmetry of a charge distribution affect the electric field lines?
-The symmetry of a charge distribution has a significant effect on the electric field lines. For symmetrical distributions, such as a point charge or a uniformly charged sphere, the field lines are also symmetrical and radiate outward uniformly from the charge. This symmetry allows for the simplification of calculations using Gauss's Law, as the field is constant over a Gaussian surface that matches the symmetry of the charge distribution.
What is the relationship between line density and the electric field in the context of Gauss's Law?
-Line density in the context of Gauss's Law refers to the number of electric field lines per unit area, and it is proportional to the electric field at a given point. The line density is also proportional to the charge that is the source of the electric field and inversely proportional to the square of the distance from the charge. This relationship allows us to equate the line density to a constant times the electric field, which is useful for calculating the electric flux through a surface.
How does Gauss's Law apply to a hollow spherical conductor?
-According to Gauss's Law, the electric field inside a hollow spherical conductor is zero. This is because the charges within a conductor rearrange themselves on the outer surface of the conductor, and there are no net charges inside to produce an electric field. The electric field is also normal to the surface of the conductor, and the surface charge density can be used to calculate the electric field at the surface.
What is the principle of superposition in electromagnetism?
-The principle of superposition states that the electric field produced by a combination of charges is the vector sum of the electric fields produced by each charge individually. This principle is crucial for calculating the resultant electric field in complex charge distributions and holds true for both static and dynamic situations, assuming the fields are linear and the superposition of fields does not lead to relativistic effects.
How does the electric field vary inside and outside a uniformly charged sphere?
-Inside a uniformly charged sphere, the electric field increases linearly with the distance from the center up to the sphere's surface. This is because the charge enclosed within a smaller sphere inside the larger one increases with the volume, which is proportional to the cube of the radius. Outside the sphere, the electric field decreases with the square of the distance from the center, following an inverse-square relationship, as if all the charge were concentrated at the center.
What is the significance of the electric field being zero inside a conductor?
-The electric field being zero inside a conductor is significant because it implies that there is no net force acting on free charges within the conductor. This state is reached when the free charges have rearranged themselves on the conductor's surface in such a way that they cancel out any external electric field. This property is fundamental to the behavior of conductors in electrostatic equilibrium and is a key concept in understanding the shielding effect of conductors.
How does the charge distribution on the surface of a conductor affect the electric field outside the conductor?
-The charge distribution on the surface of a conductor affects the electric field outside the conductor by polarizing the conductor. Charges redistribute themselves on the surface such that the electric field inside the conductor remains zero, and the electric field outside the conductor is the same as if all the charge were concentrated at the center of the conductor. This leads to a uniform electric field at a given distance from a charged spherical conductor.
What is the work function in the context of conductors?
-The work function in the context of conductors refers to the minimum amount of energy required to remove an electron from the surface of the conductor to a point in the vacuum just outside the surface. It is an important concept when considering the behavior of electrons in conductors, especially in the context of electron emission phenomena such as thermionic emission or field emission.
Why is it not necessary to perform a surface integral when calculating the electric field at a point outside a spherically symmetric charge distribution?
-It is not necessary to perform a surface integral when calculating the electric field at a point outside a spherically symmetric charge distribution because the electric field is constant over the surface of a sphere due to symmetry. The electric field at any point on the Gaussian surface (sphere) can be multiplied by the entire surface area of the sphere to find the total flux through the surface, which is a simplification of the surface integral.
What is the role of the electric field in the formation of an electrostatic equilibrium in a conductor?
-In an electrostatic equilibrium, the electric field within a conductor plays a crucial role in ensuring that the charges within the conductor redistribute themselves until the internal electric field is zero. This happens because any non-zero electric field would cause the free charges (electrons in a metal conductor) to continue moving, but in equilibrium, the charges arrange themselves in such a way that they exactly cancel out any external electric fields, resulting in no net force on the charges and thus no movement.
Outlines
📚 Introduction to Gauss's Law
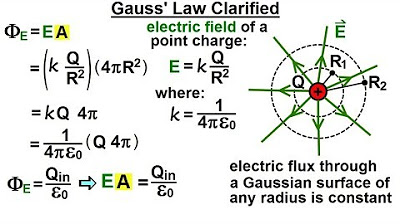
The professor begins by emphasizing the importance of Gauss's Law, not only in its application but also in understanding its derivation. He revisits the derivation to clarify concepts, focusing on the visualization of electric field lines emanating from a point charge. The discussion establishes that the number of field lines is determined by the charge's quantity and that these lines are evenly distributed in all directions due to the charge's spherical symmetry. The content of Gauss's Law is introduced through the analogy of counting these lines crossing a sphere's surface, which is foundational to the law's application.
🧲 Electric Field and Line Density Proportions
The explanation proceeds to the relationship between electric field strength and line density. It is shown that both are proportional to the charge and inversely proportional to the square of the distance from the charge, leading to the conclusion that line density is directly proportional to the electric field's magnitude. The professor uses this relationship to calculate the electric flux through a spherical surface, represented by Φ_S, which is equal to the product of line density, the constant of proportionality, and the sphere's surface area.
📐 Calculating Flux Through Surfaces
The professor then addresses the complexities of calculating the electric flux through a generic surface S', which differs from a spherical surface due to varying normal vectors and field strengths. The concept of flux is further elaborated by breaking down the surface into small elements, with the flux through each element calculated as the product of the electric field, the area vector, and the cosine of the angle between them. The principle of superposition is introduced to combine the effects of multiple charges on the electric field.
🌌 Gauss's Law for Discrete and Continuous Charge Distributions
Gauss's Law is expressed in its final form, relating the surface integral of the electric field to the total charge enclosed by the surface, divided by the vacuum permittivity (ε_0). The distinction between charges inside and outside the volume bounded by the surface is highlighted. For continuous charge distributions, the law is extended to include the volume integral of charge density, ρ, within the enclosed volume V.
🔋 Electric Field of a Uniform Charge Distribution
The application of Gauss's Law to determine the electric field of a uniformly charged sphere is explored. The professor demonstrates that the electric field outside the sphere is equivalent to that of a point charge at the center, deriving the field's radial dependence on the inverse square of the distance from the center. The case of a charge placed inside a sphere is also considered, showing that the enclosed charge is proportional to the cube of the radius, leading to a different expression for the electric field within the sphere.
🌟 Electric Field Inside and Outside a Spherical Shell
The professor discusses the electric field inside and outside a hollow spherical shell. It is shown that the field inside a hollow conductor is zero, regardless of the charge distribution on the shell, due to the cancellation of forces from symmetrically distributed charges. The argument is supported by the principle that the 1/r^2 dependence of the electric force is crucial for the field inside a hollow sphere to be zero.
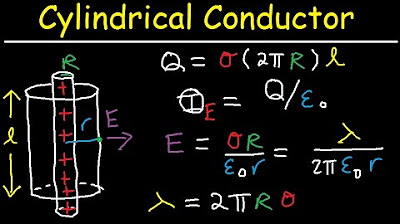
🧵 Electric Field Due to an Infinitely Long Charged Wire
The calculation of the electric field due to an infinitely long charged wire is presented. By applying Gauss's Law to a cylindrical Gaussian surface, the professor finds the electric field's magnitude to be inversely proportional to the distance from the wire, with the constant of proportionality dependent on the linear charge density.
🚫 Limitations of Gauss's Law for Complex Geometries
The professor highlights the limitations of Gauss's Law for geometries that lack symmetry. While the law simplifies calculations for symmetrical problems, it is insufficient for complex geometries where the electric field varies in strength and direction. In such cases, a full integral must be performed, potentially with computational assistance.
🏗️ Conductors and Insulators: The Behavior of Charges
The distinction between conductors and insulators is made, with conductors defined by their ability to allow free movement of negative charges. It is stated that within a static conductor, the electric field is zero, as charges redistribute until they cancel out any external field. The behavior of charges within conductors is likened to electrons in a swimming pool, unable to leave the conductor's surface but free to move within it.
🔋 Electric Field and Charge Distribution on a Conductor's Surface
The relationship between the electric field at the surface of a conductor and the surface charge density is derived using a Gaussian surface. The electric field is found to be directly proportional to the charge density, with the constant of proportionality being the vacuum permittivity (ε_0). The principle that the electric field must point perpendicular to the surface of a conductor is also discussed.
🕳️ Charge Distribution in a Conductor with a Hole
The professor explores the behavior of charges in a conductor with a hole, asserting that all charges will reside on the outer surface, with none on the inner wall of the hole. This is justified using Gauss's Law, which dictates that the enclosed charge within a conductor must be zero, leading to a complete cancellation of charges within the conductor's volume.
📝 Brief Overview of Calculating Multiple Integrals
The professor concludes with a brief overview of calculating multiple integrals in two dimensions. The process involves integrating over a region bounded by lines of constant x and y, multiplying the function by the area element dxdy. An example of calculating the area of a triangle using this method is provided, both in Cartesian coordinates and polar coordinates, emphasizing the importance of understanding the limits of integration.
Mindmap
Keywords
💡Gauss's Law
💡Electric Field
💡Flux
💡Line Density
💡Coulomb's Law
💡Superposition Principle
💡Conductor
💡Charge Density
💡Symmetry and Invariance
💡Gaussian Surface
💡Electrostatics
Highlights
Gauss's Law is crucial for understanding not just its application but also its derivation.
The visualization of Gauss's Law is straightforward, involving drawing lines of force from a point charge.
The number of lines drawn per coulomb is a matter of convention, but it must remain consistent.
Gauss's Law asserts that the number of lines crossing two different surfaces enclosing the same charge is equal.
Line density is defined as the number of lines crossing a unit area perpendicular to the lines.
The electric field's strength at a radius r is proportional to the charge and inversely proportional to the square of the radius.
The line density is proportional to the electric field, as both are proportional to q/r^2.
Gauss's Law can be applied to calculate the electric field for any surface, including those with complex geometries.
The principle of superposition simplifies the calculation of the electric field due to multiple charges.
Gauss's Law, in its final form, states that the surface integral of the electric field over a surface is equal to the charge inside divided by ε0, independent of the surface's details.
For a continuous charge distribution, Gauss's Law takes the form of a volume integral over the charge density ρ.
Gauss's Law can be used to determine the electric field of a uniformly charged sphere as if all the charge were at the center.
The electric field inside a hollow conductor is zero, regardless of the charge distribution on the outer surface.
Charges in a conductor will redistribute themselves to ensure that the electric field inside the conductor is zero.
The electric field at the surface of a conductor is perpendicular to the surface and is determined by the surface charge density.
Conductors shield the interior from external electric fields, and any charge placed on a conductor resides on the surface.
Gauss's Law provides a powerful method for calculating electric fields in symmetrical situations without the need for complex integrals.
The electric field for an infinitely long wire with a linear charge density λ is λ/2πε₀r.
Transcripts
Browse More Related Video
Physics 37.1 Gauss's Law Understood (4 of 29) Gauss' Law Clarified

Physics 37.1 Gauss's Law Understood (3 of 29) What is Gauss' Law?
Gauss Law Problems, Cylindrical Conductor, Linear & Surface Charge Denisty, Electric Field & Flux,
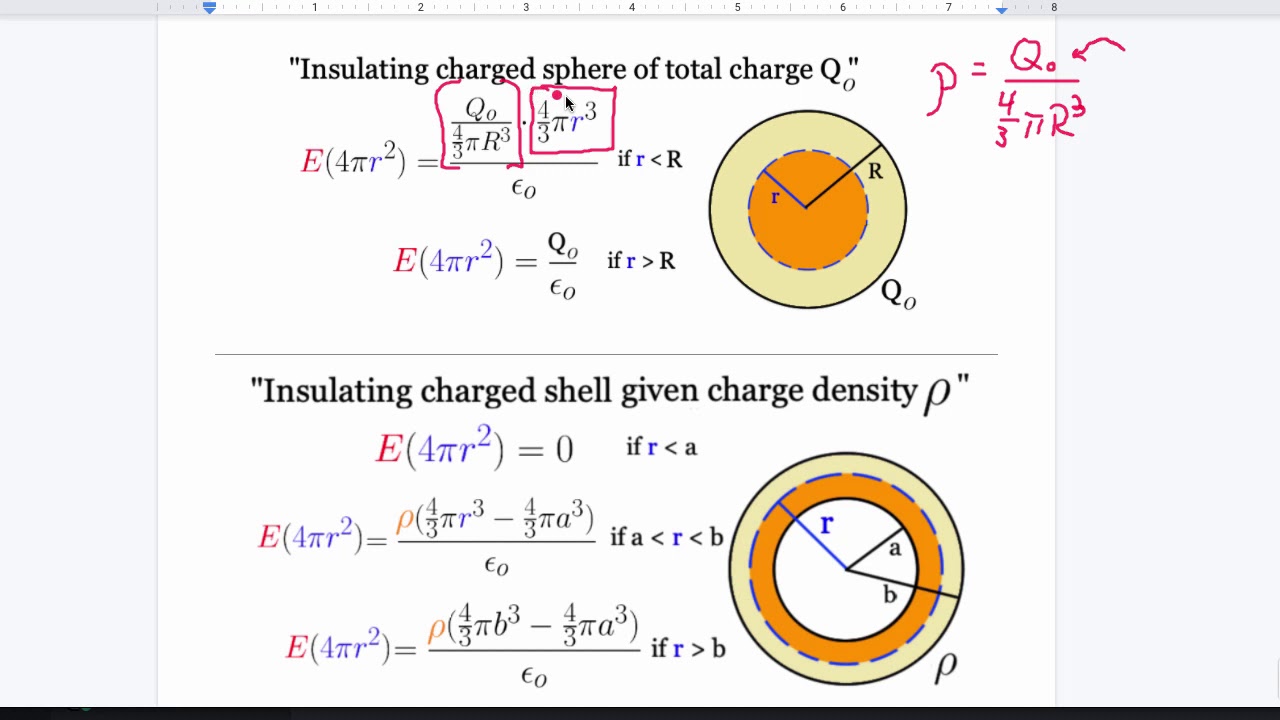
Ultimate Gauss' Law review

Gauss Law Problems - Infinite Sheet of Charge and Parallel Plate Capacitor - Physics

Electric Flux
5.0 / 5 (0 votes)
Thanks for rating: