How to Find Magnitude & Direction of Vectors
TLDRThe video script provides a comprehensive guide on understanding vectors, their difference from scalars, and how to represent them graphically. It explains that vectors have both magnitude and direction, and introduces the concept of vector components, which can be used to calculate the vector's magnitude and direction using the Pythagorean theorem and trigonometric functions. The script also includes practical examples of finding the magnitude and direction of given vectors, emphasizing the use of polar coordinates and unit circle angles to accurately describe vector properties.
Takeaways
- 📌 Vectors are quantities with both magnitude and direction, such as position, displacement, velocity, and acceleration.
- 📏 Scalars, on the other hand, only have magnitude like time, money, and mass without any direction.
- 🖊️ To represent a vector graphically, draw an arrow where the length indicates magnitude and the direction is shown by the arrowhead.
- 🔑 The variable representing the vector's length is typically denoted by a letter (like 'a') with the vector symbol (→) above it.
- 👉 When discussing only the magnitude of a vector, it can be represented with absolute value bars or the letter without the vector symbol.
- 📐 Vectors have components which can be thought of as coordinates; these are the x (horizontal) and y (vertical) parts of the vector.
- 🔺 The components of a vector can be used to form a right triangle, allowing the application of trigonometry and the Pythagorean theorem.
- 🧮 To calculate the magnitude of a vector, use the formula: √(x component² + y component²).
- 📍 To find the direction (angle) of a vector, use the tangent inverse of the y component divided by the x component.
- 🤝 Understanding vector components is crucial for solving problems involving vector magnitude, direction, and their relationships.
- 📊 Example problems in the script demonstrate how to find the magnitude and direction of vectors A, B, and C using their components.
Q & A
What is the primary difference between a vector and a scalar?
-A vector has both magnitude and direction, such as position, displacement, velocity, and acceleration, while a scalar has only magnitude, like time, money, and mass.
How is a vector represented graphically?
-A vector is represented by an arrow, where the length of the arrow signifies the magnitude and the direction of the arrowhead indicates the direction of the vector.
What does the length of the arrow in a vector represent?
-The length of the arrow in a vector represents the magnitude of the vector.
How is the direction of a vector denoted?
-The direction of a vector is denoted by the arrowhead and is typically represented by the angle theta.
What is the standard notation for representing a vector?
-A vector is usually represented by a letter, such as 'a', with an arrow above the letter indicating it's a vector. To denote just the magnitude, absolute value bars are used or the letter is written without the arrow.
How can you express a vector in terms of its components?
-A vector can be expressed in terms of its x (horizontal) and y (vertical) components, written as 'a = (ax, ay)', which are analogous to the coordinates of the vector.
What is the relationship between the components of a vector and the Pythagorean theorem?
-The components of a vector can be related to the Pythagorean theorem, where the magnitude of the vector is the square root of the sum of the squares of its components (a = sqrt(ax^2 + ay^2)).
How do you calculate the magnitude of a vector given its components?
-To calculate the magnitude of a vector from its components, you use the formula: magnitude = sqrt((component x)^2 + (component y)^2).
How do you find the direction angle of a vector from its components?
-The direction angle (theta) of a vector from its components can be found using the tangent inverse function: theta = tan^(-1)(component y / component x).
What should be considered when finding the angle of a vector in different quadrants?
-When finding the angle of a vector in quadrants other than the first or fourth, you must adjust the angle found using the tangent inverse by adding or subtracting 180 degrees to determine the correct angle based on the quadrant.
How can you convert the unit circle angle to the actual angle of a vector?
-To convert the unit circle angle to the actual angle of a vector, you must consider the quadrant in which the vector lies. If the vector is in the second or third quadrant, add 180 degrees to the unit circle angle. If it's in the fourth quadrant, the unit circle angle is negative, indicating the direction is below the x-axis.
What is the significance of the Pythagorean theorem in vector analysis?
-The Pythagorean theorem is significant in vector analysis as it allows you to find the magnitude of a vector and understand the relationship between its components in a two-dimensional space, which is essential for solving various vector-related problems.
Outlines
📐 Introduction to Vectors and Scalars
This paragraph introduces the fundamental concepts of vectors and scalars. A vector is characterized by both magnitude and direction, examples include position, displacement, velocity, and acceleration. Scalars, on the other hand, possess only magnitude, such as time, money, and mass. The distinction is clarified with an example of velocity, where 30 miles per hour can have different directions, but mass cannot have a directional component. The paragraph also explains how to graphically represent vectors using arrows on a coordinate system, where the length of the arrow denotes magnitude and the arrowhead indicates direction. The use of the Greek letter theta (θ) to represent direction is introduced.
📐 Vector Representation and Components
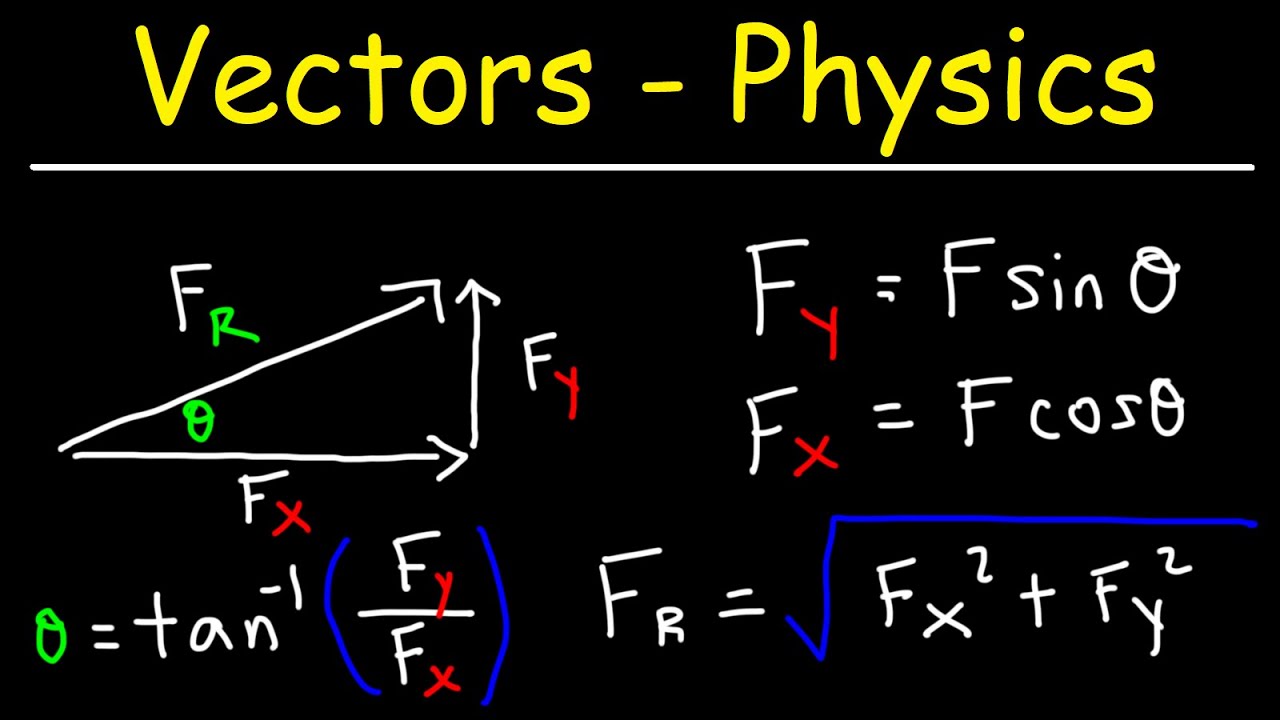
The paragraph delves into the specifics of representing vectors both graphically and algebraically. It explains how vectors are named and denoted, using letters with an arrow to indicate vector status. The concept of vector components is introduced, likening them to the x and y coordinates in a coordinate system. The components are referred to as 'ax' for the horizontal (x) component and 'ay' for the vertical (y) component. The paragraph also covers how to calculate the magnitude of a vector using the Pythagorean theorem with the components, and how to find the direction angle using the tangent inverse of the y component over the x component. The explanation is supplemented with an example to illustrate the process.
📐 Calculating Magnitude and Direction of Vectors
This section focuses on the practical application of calculating the magnitude and direction of vectors using their components. The process involves squaring the x and y components, summing these values, and then taking the square root to find the magnitude. To determine the direction angle, the tangent inverse of the y component divided by the x component is used. The paragraph provides a step-by-step example for three vectors, a, b, and c, showing how to apply these formulas. It also addresses the concept of unit circle angles and how to adjust them based on the quadrant in which the vector lies, emphasizing the importance of using the correct mode (degree or radian) on a calculator.
📐 Drawing Vectors Using Components
The final paragraph demonstrates how to draw vectors based on their algebraic representation. It reiterates the process of using the x and y components to pinpoint the vector's location on a coordinate system. The magnitude is calculated using the Pythagorean theorem, and the direction angle is found using the tangent inverse method. The paragraph reinforces the concept by drawing a vector with specific components and explaining how to determine its position and direction relative to the coordinate axes. The explanation concludes with a succinct summary of the vector representation process, tying together the concepts discussed throughout the video script.
Mindmap
Keywords
💡vectors
💡scalars
💡magnitude
💡direction
💡components
💡arrow representation
💡Pythagorean theorem
💡tangent inverse
💡unit circle
💡polar coordinate
Highlights
Vectors are defined as having both magnitude and direction, unlike scalars which only have magnitude.
Examples of vectors include position, displacement, velocity, and accelerations, while examples of scalars include time, money, and mass.
To represent a vector graphically, an arrow is used where the length of the arrow symbolizes the magnitude and the direction is indicated by the arrowhead.
The variable representation of a vector involves placing the vector's name near the head of the arrow and using a little arrow above the letter to denote it as a vector.
The magnitude of a vector can be represented using absolute value bars or simply by the letter without an arrow when discussing only the length.
Vector components are analogous to the x and y coordinates, with a vertical component (sub y) and a horizontal component (sub x).
The components of a vector can be used to form a right triangle, allowing the application of the Pythagorean theorem for vector analysis.
The magnitude of a vector is calculated using the square root of the sum of the squared components (ax squared plus ay squared).
The direction of a vector is found using the inverse tangent of the y component over the x component (tan^-1(ay/ax)).
Unit circle angles can sometimes be misleading due to the quadrant in which the vector lies, requiring adjustments to ensure the correct angle is used.
For vectors in the second or third quadrant, the unit circle angle must be adjusted by adding 180 degrees to get the correct angle.
When expressing a vector using its magnitude and direction, it is referred to as polar coordinate representation.
The video provides a comprehensive guide on how to draw vectors and calculate their magnitude and direction using components.
The method for finding the magnitude and direction of a vector is demonstrated through example problems with vectors a, b, and c.
The video emphasizes the importance of understanding vector components and their application in solving vector-related problems.
The practical application of the Pythagorean theorem and trigonometric functions in vector analysis is thoroughly explained.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: