Introduction to Logarithms (1 of 2: Definition)

Eddie Woo
30 Aug 201707:52
EducationalLearning
32 Likes 10 Comments

TLDRThe video script introduces logarithms as an alternative perspective on exponential growth, using the concept of time and growth rate to explain how logarithms can reframe the understanding of exponential functions. It illustrates this with examples, such as doubling sequences and their corresponding logarithmic expressions, highlighting the relationship between growth rate, final size, and time. The script effectively uses the analogy of a 'doubling machine' to clarify the mathematical principles behind logarithms and their applications.

Takeaways
  • 📈 Logarithms offer an alternative perspective on exponentials, allowing us to understand growth and change in a different way.
  • 🔢 Exponentials, like 2 to the power of 5, represent repeated multiplication of a number (doubling in this case) over a certain period or 'power'.
  • 📊 The 'exponent' or 'index' or 'power' indicates how many times the base number is multiplied by itself.
  • 🕰️ The concept of growth rate and time can be applied to understand exponentials, where the exponent represents the duration of growth at a constant rate.
  • 🔄 The number 2 to the power of 0 equals 1, demonstrating that no growth or change has occurred.
  • 🔙 Negative exponents represent a reverse growth rate, effectively shrinking the base number, as in the example of 1/2 (half the size).
  • 📐 The logarithmic form of an exponential equation is written as 'log base b of x equals y', which can be read as 'the logarithm of x to the base b equals y'.
  • 🔄 Logarithmic equations can be converted back to exponential form, simply by rearranging the terms and using the definition of logarithms.
  • 📈 Understanding logarithms and exponentials is key to solving problems related to growth, time, and change.
  • 🔢 The base of a logarithm indicates the rate of growth or change, as seen in the example of tripling (base 3) leading to a final size of 81 after four steps.
  • 🌐 The analogy of time and growth helps to visualize and comprehend the abstract concepts of logarithms and exponentials.
Q & A

  • What is the main concept introduced in the transcript?

    -The main concept introduced in the transcript is logarithms, which is a way of looking at exponentials or indices differently.

  • How are exponentials related to the concept of growth?

    -Exponentials are related to the concept of growth in that they represent a growth rate. For example, 2 to the power of 5 (2^5) represents a growth process where the number 2 is doubled 5 times, resulting in 32.

  • What does the number 5 represent in the exponential 2^5?

    -In the exponential 2^5, the number 5 represents the exponent or the power, indicating how many times the base (2) is multiplied by itself during the growth process.

  • What is the significance of the number 32 in the context of 2^5?

    -The number 32 in the context of 2^5 signifies the final result or the size after the growth process, which is 2 doubled 5 times.

  • How does the zero exponent (2^0) relate to the concept of growth?

    -A zero exponent (2^0) in the context of growth means that there has been no growth at all, resulting in the base value, which is 1 (100% of the original size).

  • What does a negative exponent represent in terms of growth?

    -A negative exponent represents a reversal of the growth process. For example, 2 to the power of -1 (2^-1) would mean going back in time in a growing machine that doubles in size, resulting in half the size (1/2) of the original.

  • How is the concept of logarithms related to the concept of time in the transcript?

    -Logarithms are related to the concept of time in that they can be used to determine the duration of a growth process. If you know the growth rate (base) and the final size, you can calculate the time it took to reach that size using logarithms.

  • What is the mathematical notation for a logarithm as described in the transcript?

    -The mathematical notation for a logarithm as described in the transcript is 'log base b of x equals y', which is written as 'log_b(x) = y'. Here, b is the base, x is the number being logged, and y is the result or the exponent.

  • How can you convert a logarithmic equation back to an exponential equation?

    -To convert a logarithmic equation back to an exponential equation, you rearrange the equation by recognizing that the base raised to the power of the logarithm result equals the number being logged. For example, if 'log base 2 of 32 equals 5', it can be rewritten as '2^5 = 32'.

  • What is the result of the logarithmic equation 'log base 2 of 32 equals 5'?

    -The result of the logarithmic equation 'log base 2 of 32 equals 5' is that it confirms the number 32 is 2 raised to the power of 5, which means it took 5 steps of doubling the base (2) to reach 32.

  • How does changing the base in logarithms affect the growth rate?

    -Changing the base in logarithms affects the growth rate by changing the factor by which the number is multiplied in each step. For example, a base of 3 in 'log base 3 of 81 equals 4' indicates a growth rate where the number is tripled (multiplied by 3) in each step to reach 81.

  • What is the significance of the base in a logarithmic equation?

    -The base in a logarithmic equation is significant as it represents the number by which the value is being multiplied during the growth process. The base determines the growth rate or the factor of increase in each step of the growth.

Outlines
00:00
📈 Introduction to Logarithms and Exponential Growth

This paragraph introduces the concept of logarithms as a way of understanding exponential growth or decay. It begins by explaining the basic definition of logarithms and their relation to exponentials and indices. The speaker uses the example of 2 to the power of 5, which equals 32, to illustrate the concept of growth rate and time. The explanation continues with the introduction of the index law, highlighting how any number to the power of 0 equals 1, and negative powers are discussed in the context of time reversal and shrinking size. The paragraph concludes with the analogy of a growth machine, transitioning into the next part where logarithms will be explored in more detail.

05:01
🔢 Understanding Logarithms Through Time and Growth Analogy

In this paragraph, the speaker delves deeper into the concept of logarithms by using the analogy of time and growth. The discussion focuses on how changing the perspective from exponential form to logarithmic form can provide new insights. The speaker rewrites the previous exponential examples as logarithmic equations, such as log base 2 of 32 equals 5, and log base 2 of 1/2 equals -1, to demonstrate the relationship between growth rate, final size, and time. The explanation also includes another example with a different base, log base 3 of 81 equals 4, to show how the base affects the rate of growth. The paragraph emphasizes the importance of understanding the relationship between growth rate, final size, and time in the context of logarithms and exponentials.

Mindmap
Keywords
💡Logarithms
Logarithms are a mathematical concept that allows us to express the power or exponent to which a number (the base) must be raised to obtain a certain value. In the video, logarithms are introduced as a way of looking differently at exponentials or indices, providing an alternative perspective on growth and time. For instance, the script explains that log base 2 of 32 equals 5, which means that the number 2 needs to be multiplied by itself 5 times to result in 32.
💡Exponentials
Exponentials, or exponential functions, are expressions that represent the growth or decay of a quantity at a constant rate. In the context of the video, exponentials like 2 to the power of 5, which equals 32, are used to illustrate the concept of growth and doubling. The video emphasizes understanding the meaning behind these expressions, such as the 'exponent' representing the number of times the base is multiplied by itself.
💡Growth Rate
The growth rate refers to the speed at which a value increases. In the video, the growth rate is used as a metaphor to understand the process of exponentials and logarithms. For example, a growth rate of doubling is used to explain how the number 2, when multiplied by itself, grows over time. The concept is crucial in understanding how logarithms can be used to calculate the time it takes for a quantity to reach a certain size at a given growth rate.
💡Time
Time, in the context of the video, is analogous to the number of iterations or periods it takes for a quantity to grow or change by a certain factor. The video uses the concept of time to explain how logarithms can help determine the duration of growth when the growth rate and the final size are known. For instance, if you know that a quantity doubles in size and ends up being 32 times bigger, you can use logarithms to find out it took 5 periods of growth.
💡Base
In the context of the video, the base is the number that is used as a foundation for exponential growth or the number to which the exponent is applied in logarithmic expressions. For example, in the logarithmic expression 'log base 2 of 32 equals 5,' the base is 2, which means that the number 2 is the value by which growth occurs in each iteration.
💡Exponent
An exponent, also referred to as the index or power, indicates the number of times a base is multiplied by itself in an exponential expression. In the video, the exponent is used to explain the concept of growth, where the exponent represents how many times the doubling occurs. For instance, in '2 to the power of 5,' the exponent is 5, signifying that the base 2 is multiplied by itself 5 times to result in 32.
💡Doubling
Doubling is a specific type of growth where a quantity increases to twice its original size with each iteration or period. In the video, doubling is used as an example of a growth rate to illustrate how exponentials and logarithms work. The concept is used to explain how the base number, when doubled a certain number of times as indicated by the exponent, results in a final value.
💡Negative Power
A negative power, as discussed in the video, refers to a situation where a number is raised to a power that is less than zero. This is analogous to shrinking or reducing in size, as opposed to growth. For example, the script mentions 'a half' which is equivalent to a negative power, indicating that instead of growing, the quantity is reduced to half its size. This concept is used to further explain the analogy of time and growth in logarithms.
💡Index Law
The index law mentioned in the video is a fundamental property of exponents that states any number raised to the power of zero equals one. This is used to illustrate the concept of no growth or no change over time. In the context of logarithms, the index law helps to reinforce the idea that if the base remains constant and the result is one, then there has been no growth or change in size.
💡Metaphor
Metaphor is a figure of speech that makes a comparison between two unlike things. In the video, the metaphor of time and growth is used to help the viewer understand the abstract concepts of logarithms and exponentials. By comparing the process of exponential growth to a journey through time, the video makes these mathematical concepts more relatable and easier to grasp.
💡Calculator
A calculator is a device or software used to perform mathematical calculations, including complex operations like exponentiation and logarithms. In the video, the mention of a calculator is to emphasize the practical application of logarithms and exponentials. It suggests that while the concepts can be understood and applied conceptually, they can also be verified and calculated precisely using a calculator.
Highlights

Logarithms are introduced as a way of looking at exponentials or indices differently.

Exponentials represent a concept of growth or doubling in size, exemplified by 2 to the power of 5.

The exponent or index signifies the growth rate and the number of times the doubling occurs.

An exponential expression like 2 to the power of 5 can be thought of as a growth rate over time.

The concept of zero as an exponent indicates no growth or the original size, as in 2 to the power of 0 equals 1.

Negative exponents, such as 1/2, represent shrinking or going backwards in time in the context of growth.

Logarithms are a mathematical tool to reframe exponential expressions, changing the perspective of the problem.

The logarithmic expression log base 2 of 32 equals 5 is used to determine the time it takes to reach a certain size at a given growth rate.

Understanding logarithms allows one to calculate the time it takes to grow from an original size to a final size at a constant rate.

The base in a logarithmic expression represents the growth rate or the number that is being multiplied by itself.

Changing the base of a logarithm, such as from 2 to 3, changes the rate of growth from doubling to tripling.

The process of converting a logarithmic expression to an exponential one involves swapping the base and the result.

The concept of logarithms and exponentials is essential for understanding growth and decay processes in various fields.

The analogy of time and growth helps to understand the meaning behind logarithmic and exponential expressions.

Logarithms and exponentials are fundamental concepts in mathematics with wide applications in science, engineering, and finance.

The mathematical sentence log base 2 of 32 equals 5 can be used to solve for the time of growth when the growth rate and final size are known.

Understanding the relationship between exponents, logarithms, and their bases is crucial for solving problems involving growth and change.

Transcripts

Browse More Related Video

Business Calculus -- Math 1329 -- Section 4.2 -- Logarithmic Functions

Exponential Growth and Decay (Precalculus - College Algebra 66)

AP Calculus AB - 7.8 Exponential Models With Differential Equations

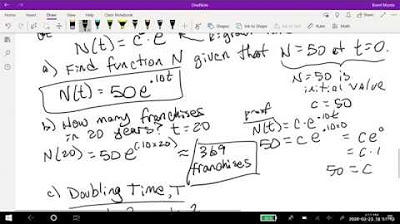
Math 11 - Section 2.4 (previously section 3.3)

Logarithms explained Bob Ross style

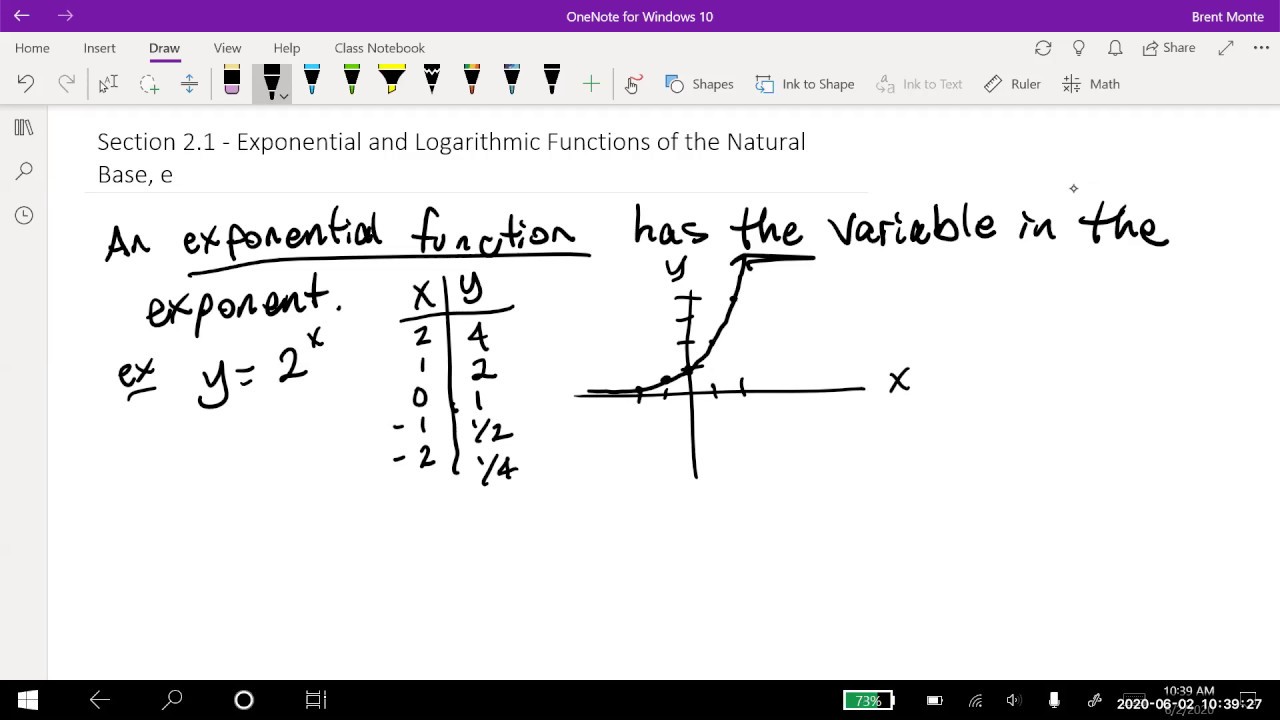
Math 11 - Section 2.1

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Math ConceptsExponential GrowthLogarithmic FunctionsEducational AnalogiesBase and PowersMathematics EducationGrowth RateTime and ProgressDoubling and Tripling