Math 11 - Section 2.4 (previously section 3.3)

Professor Monte

23 Mar 202062:09

EducationalLearning

32 Likes 10 Comments

TLDRThis video script delves into the applications of uninhibited and limited growth models in calculus, focusing on their practical implications in business and population growth. The presenter explains the unique properties of exponential functions, where the derivative of such a function is a constant multiple of the original function. Using the example of a business growing at a 12% rate per year, the script illustrates how to model growth and calculate the number of franchises after a certain period. It also addresses the concept of doubling time and its formula, showing how to calculate the time it takes for a quantity to double at a given growth rate. The video further explores the limited growth model, which is characterized by a growth that approaches a limit over time, and applies it to a historical population growth scenario on Pitcairn Island. The presenter uses the logistic equation to forecast population sizes at various time intervals and discusses the rate of change in population. The script concludes with the calculation of the limiting population size, which is the maximum population the island can sustain indefinitely.

Takeaways

📈 The derivative of an exponential growth function, like f(x) = Ce^(Kx), is a constant times the original function, where the constant is the growth rate K.
💡 The function e^x is unique in that its derivative is the function itself, which is a key property used in modeling growth problems.
📚 In business applications, growth rates can be modeled using exponential functions, where the growth is a percentage of the current amount.
🔍 The constant C in the exponential function represents the initial amount at time x = 0, which is crucial for determining the specific function that fits a given growth scenario.
✅ The general form of an exponential growth function is P(x) = Ce^(Kx), where P(x) is the amount at time x, C is the initial amount, and K is the growth rate.
🌱 The concept of doubling time relates to the time it takes for an initial amount to double at a constant growth rate, which is calculated using the formula T = ln(2) / K.
📊 For exponential growth represented by n(t) = Ce^(Kt), the number of franchises or items after a certain time T can be calculated by substituting T into the formula.
🤔 The limit of exponential growth functions as time goes to infinity is approached by using the formula P(T) ≈ C/(1 + Be^(-KT)), where B is a constant and K is the growth rate.
🧮 The derivative of a limited growth model, which can be represented by P(T) = C/(1 + Be^(-KT)), can be found using the product rule and provides the rate of change of the population or quantity over time.
🏞️ The limited growth model is useful for situations where growth is expected to level off, such as population growth in an environment with limited resources.
⏳ The limiting value of a population, which is the maximum stable population size, can be found by considering the behavior of the growth model as time T approaches infinity.

Q & A

What is unique about the function f(X) = 70^(5x) when taking its derivative?
-The derivative f'(X) results in the original function multiplied by a constant. Specifically, f'(X) = 5 * f(X), which is unique to functions of the form e^(kx), where k is a constant.
How can the growth rate of a business be modeled mathematically?
-The growth rate can be modeled using an exponential function. If the growth rate is a certain percentage per time period, the function can be represented as P(X) = C * e^(kX), where C is the initial amount, k is the growth rate, and X is the time.
What is the significance of the constant C in the context of the exponential growth function?
-The constant C represents the initial value of the function at time X equals 0. It is always equal to the initial amount before any growth occurs.
How can you find the number of franchises after a certain number of years given a growth rate?
-You can use the formula n(T) = C * e^(kT), where n(T) is the number of franchises at time T, C is the initial number of franchises, k is the growth rate, and T is the time in years.
What is the doubling time formula for an exponential growth function?
-The doubling time formula is T = ln(2) / k, where T is the time it takes for the initial amount to double, and k is the growth rate.
How can you estimate the net sales of a company in a future year given an annual growth rate?
-You can use the formula S(T) = S0 * e^(kT), where S(T) is the estimated sales at time T, S0 is the initial sales, k is the annual growth rate, and T is the number of years since the initial sales were recorded.
What is the relationship between the derivative of a function and its growth rate in the context of exponential growth?
-The derivative of an exponential growth function represents the growth rate at any given time. If the derivative is a constant times the function itself, it indicates exponential growth.
How does the limited growth model differ from the uninhibited growth model?
-The limited growth model has an upper bound or limit, represented by a horizontal asymptote, whereas the uninhibited growth model continues to grow exponentially without any limit.
What is the general formula for the limited growth model?
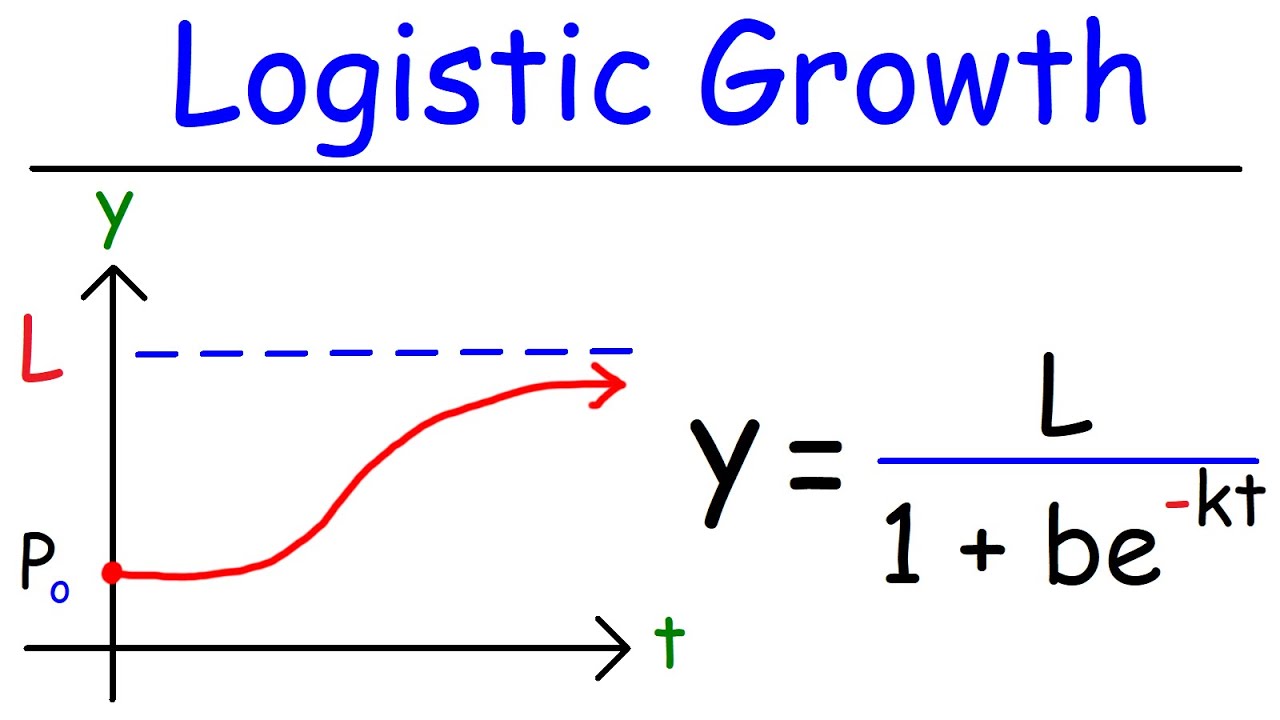
-The general formula for the limited growth model is P(T) = L / (1 + (B * e^(-kT))), where P(T) is the population at time T, L is the limiting value, B is a constant, k is the growth rate, and T is the time.
How can you find the limiting value of a population on an island using the limited growth model?
-As T approaches infinity, the term (B * e^(-kT)) approaches 0, so the limiting value L is the initial population divided by (1 + 0), which simplifies to the initial population value.
What is the rate of change of the population in the limited growth model?
-The rate of change, or derivative P'(T), can be found using the product rule for differentiation. It represents the growth rate of the population at any given time T.

Outlines

00:00

📈 Exponential Growth Functions and Derivatives

This paragraph introduces the concept of exponential growth functions and their unique property where the derivative of the function is a constant multiple of the original function. It uses the function f(X) = 70^(5x) as an example to illustrate this, showing that its derivative is 5 times the function itself. The paragraph also connects this mathematical concept to a business application, discussing how growth rates can be modeled using similar exponential functions.

05:02

📚 Newton's and Leibnitz's Notations in Calculus

The second paragraph discusses the two notations used in calculus: Newton's notation and Leibnitz's notation. It explains that if a function's derivative is a constant times the function itself, it can be expressed in either notation as F'(x) = kF(x) or dy/dx = ky, where k is the constant growth rate. The paragraph also demonstrates how to find the constant C in the function by using the initial value of the function at a given point.

10:03

🍕 Franchise Expansion Model with Exponential Growth

This paragraph applies the concept of exponential growth to a business scenario where a company is expanding its franchises across the country. It outlines how the number of franchises (n) is expected to increase at a rate of 10% per year, which is the derivative of n with respect to time (T). The paragraph then shows how to find the function that represents this growth, assuming an initial number of franchises and using the growth rate to model future expansion.

15:05

📊 Calculating Future Franchise Numbers and Doubling Time

The fourth paragraph focuses on calculating the number of franchises after a certain number of years using the previously established exponential growth model. It also covers how to determine the doubling time of the initial number of franchises, using a formula that relates the growth rate to the time it takes for the initial amount to double.

20:05

💰 Application of Uninhibited Growth Model in Finance

The fifth paragraph explores the application of the uninhibited growth model in financial contexts, such as when money is compounded continuously. It explains how to calculate the annual interest rate if it's known that money will double in a certain number of years, using the natural exponential function and the concept of doubling time.

25:06

📊 Doubling Time Formula and Its Derivation

This paragraph delves into the derivation of the doubling time formula, which is used to calculate the time it takes for an initial amount to double at a constant growth rate. It also discusses the reverse application of the formula to find the growth rate needed to double in a given time frame.

30:07

📈 Estimating Sales with Exponential Growth

The sixth paragraph applies the concept of exponential growth to estimate the sales of a company, Green Mountain Coffee Roasters, which has been growing at an annual rate of 46.3%. It demonstrates how to calculate the function that models the sales over time, given the initial sales and the growth rate, and how to estimate the sales in a specific year.

35:09

💸 Doubling Time in Business Growth

This paragraph continues the financial application of exponential growth by calculating the doubling time for the company's sales, given the high growth rate. It shows that the company doubles its sales approximately every 1.5 years, indicating rapid growth.

40:09

🏦 Hardy Bank's Continuous Compounding Interest Rate

The seventh paragraph addresses a scenario where a bank advertises continuous compounding and a doubling of investment in twelve years. It calculates the annual interest rate required to achieve this doubling time using the natural exponential function and the doubling time formula.

45:10

🌱 Limited Growth Model and Its Characteristics

The eighth paragraph introduces the limited growth model, which differs from the uninhibited growth model by having an upper limit or horizontal asymptote. It explains the general formula for the limited growth model and discusses its behavior as time approaches infinity.

50:11

📉 Demonstrating the Approach to Zero in Limited Growth

This paragraph provides a numerical demonstration of how a component of the limited growth model approaches zero as time goes to infinity. It uses an example with specific values to illustrate the concept and reinforces the idea that the model flattens out over time, reaching an upper limit.

55:12

🌐 Application of the Limited Growth Model to Population Dynamics

The ninth paragraph discusses an application of the limited growth model to population dynamics, specifically the growth of the human population on the island of Pitcairn. It outlines how to calculate the population at different time points using the logistic equation and addresses a correction in the book's formula.

00:13

📉 Calculating Population Growth and the Derivative

The tenth paragraph focuses on calculating the population growth on Pitcairn Island after a certain number of years using the logistic equation. It also covers how to find the rate of change in the population, applying the product rule for derivatives, and discusses the limitations of exponential growth.

🏔️ Finding the Limiting Population Size on Pitcairn Island

The final paragraph concludes the discussion on the limited growth model by calculating the limiting population size on Pitcairn Island as time approaches infinity. It reinforces the concept that the population growth will eventually stabilize at a certain maximum value, which is derived from the logistic equation.

Mindmap

Keywords

💡Derivative

The derivative is a fundamental concept in calculus that represents the rate of change of a function with respect to its variable. In the video, the derivative is used to model growth rates, such as the rate at which a business or population grows over time. It is exemplified by expressions like 'P prime of X' or 'dN/dt', which represent the rate of change of a quantity (like profit or number of franchises) with respect to another (like time or years).

💡Exponential Growth

Exponential growth is a specific way that a quantity can increase over time, where the growth rate is proportional to the current value of the quantity. The video discusses exponential growth in the context of business applications, such as the growth of franchises or sales of a company. It is characterized by the formula 'C * e^(K*T)', where C is the initial value, K is the growth rate, and T is time.

💡Chain Rule

The chain rule is a fundamental theorem in calculus used to compute the derivative of a composite function. In the video, the chain rule is mentioned in the context of finding the derivative of an exponential function, such as 'e to the 5x', where the derivative involves multiplying the exponential function by the derivative of the exponent.

💡Continuous Compounding

Continuous compounding refers to the process where an interest rate is applied repeatedly over a period of time, with the frequency of compounding approaching infinity. In the video, continuous compounding is used to discuss how money can grow without bound, as exemplified by the formula 'e^(rt)', where 'e' is the base of the natural logarithm, 'r' is the interest rate, and 't' is time.

💡Logarithm

A logarithm is the inverse operation to exponentiation, used to solve equations involving exponential growth or decay. In the video, logarithms are used to derive the doubling time formula, which is 'T = ln(2) / K', where 'T' is the time it takes for a quantity to double, 'ln' is the natural logarithm, and 'K' is the growth rate.

💡Doubling Time

Doubling time is the period it takes for an initially small quantity to double in size. It is a concept used in the video to discuss how quickly a population or investment can grow. The formula for doubling time is derived from the concept of exponential growth and is used to estimate, for example, how many years it will take for a population to double in size.

💡Limiting Value

The limiting value is the value that a function approaches as the input (often time) goes to infinity. In the context of the video, the limiting value is used to determine the maximum population size that an environment can sustain, which is a key concept in the limited growth model discussed towards the end of the transcript.

💡Uninhibited Growth Model

The uninhibited growth model is a mathematical model that describes a quantity growing without any constraints. In the video, it is represented by the exponential function 'e^(K*T)', where growth is expected to continue indefinitely without any upper limit. This model is contrasted with the limited growth model, which incorporates an upper bound.

💡Limited Growth Model

The limited growth model is a mathematical model that describes growth that slows as it approaches a certain limit. It is represented by the logistic function 'P(T) = K/(c + (K-c)e^(-r*T))', where 'K' is the carrying capacity or limit. In the video, this model is used to discuss population growth that levels off as it approaches the carrying capacity of the environment.

💡Newton's Notation and Leibnitz Notation

These are two different notations used in calculus to represent derivatives. Newton's notation uses a dot (e.g., 'P prime of X') to denote a derivative, while Leibnitz's uses 'd/dx' (e.g., 'dy/dx'). In the video, both notations are mentioned as ways to express the derivative of a function, which is crucial for understanding rates of change and growth.

💡Carrying Capacity

Carrying capacity refers to the maximum population size of a species that an environment can sustain indefinitely. It is a key concept in the limited growth model. In the video, the carrying capacity is used to discuss the maximum number of people that can live on an island without depleting its resources, as represented by the limiting value in the logistic equation.

Highlights

The unique property of exponential functions where the derivative is a constant times the original function is discussed.

The concept of modeling business growth using exponential functions and their derivatives is introduced.

An example of a business application with a 12% growth rate modeled by an exponential function is provided.

Derivatives of exponential functions are shown to fit an exponential form, leading to the general formula for such growth models.

The constant C in the exponential model is identified as the initial amount of the function.

A problem from a textbook is solved, illustrating how to find the function that models the growth of franchises with a 10% annual increase.

The calculation of the number of franchises after 20 years using the derived exponential function is demonstrated.

The doubling time formula for exponential growth is introduced and applied to find the period it takes for the initial number of franchises to double.

An application of exponential growth to annual net sales is shown, with a growth rate of 46.3% per year.

Estimation of sales in 2012 and the doubling time for the sales growth are calculated using the exponential growth model.

The concept of continuous compounding and its relation to the exponential function e^x is explained.

A formula to calculate the annual interest rate for continuous compounding that results in a doubling of money in a given time frame is provided.

The limited growth model, characterized by an S-shaped curve approaching a horizontal asymptote, is introduced.

The logistic growth equation is explained as a model for populations that cannot grow indefinitely due to limitations such as food supply.

An example using the logistic growth equation to estimate the population on Pitcairn Island after various years is worked through.

The rate of change of the population is calculated using the derivative of the logistic growth equation.

The limiting value of the population, which the function approaches as time goes to infinity, is determined to be 200 people.

Transcripts

Browse More Related Video

Logistic Growth Function and Differential Equations

Logistic growth versus exponential growth | Ecology | AP Biology | Khan Academy

Exponential Growth and Decay Calculus, Relative Growth Rate, Differential Equations, Word Problems

Exponential and logistic growth in populations | High school biology | Khan Academy

Logistic Growth

The Logistic Equation and the Analytic Solution

Related Tags

Growth Models Exponential Functions Business Application Profit Modeling Population Dynamics Sales Growth Derivatives Calculus Continuous Compounding Uninhibited Growth Limited Growth